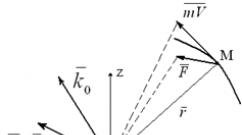
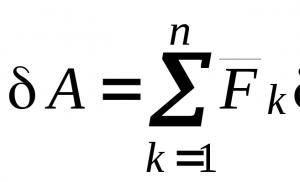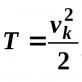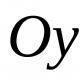Tangen dan permukaan normal online. Materi teori. Bagaimana menulis persamaan bidang singgung dan normal pada suatu titik jika permukaan diberikan oleh fungsi eksplisit?

1 °

1 °. Persamaan bidang singgung dan normal untuk kasus spesifikasi eksplisit permukaan.

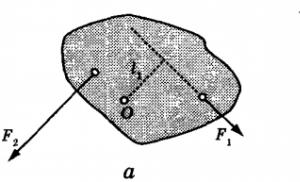
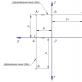
Pertimbangkan salah satu aplikasi geometris turunan parsial dari fungsi dua variabel. Biarkan fungsinya z = F (x;y) terdiferensiasi pada titik (x 0; di 0) beberapa daerah DÎ R2... Mari kita potong permukaannya S, fungsi pencitraan z, pesawat terbang x = x 0 dan y = y 0(gambar 11).

Pesawat NS = x 0 melintasi permukaan S sepanjang beberapa baris z 0 (y), yang persamaannya diperoleh dengan mensubstitusikan fungsi aslinya ke dalam ekspresi z ==F (x;y) dari pada NS angka-angka x 0. Titik M 0 (x 0;y 0,F (x 0;y 0)) termasuk dalam kurva z 0 (y). Berdasarkan fungsi terdiferensiasi z pada intinya M 0 fungsi z 0 (y) juga terdiferensiasi pada titik y = y 0. Oleh karena itu, pada titik ini di pesawat x = x 0 ke kurva z 0 (y) garis singgung dapat ditarik l 1.

Melakukan alasan serupa untuk bagian pada = pada 0, membangun tangen l 2 ke kurva z 0 (x) pada intinya NS = x 0 - Langsung 1 1 dan 1 2 tentukan bidang yang disebut bidang singgung ke permukaan S pada intinya M 0.

Mari kita buat persamaannya. Karena pesawat melewati titik Mo (x 0;y 0;z 0), maka persamaannya dapat ditulis sebagai

A (x - xo) + B (y - yo) + C (z - zo) = 0,

yang dapat ditulis ulang seperti ini:

z -z 0 = A 1 (x - x 0) + B 1 (y - y 0) (1)

(membagi persamaan dengan -C dan menunjukkan ).

Menemukan 1 dan B1.

persamaan tangen 1 1 dan 1 2 memiliki bentuk

masing-masing.

Garis singgung l 1 terletak di pesawat a , oleh karena itu, koordinat semua titik l 1 memenuhi persamaan (1). Fakta ini dapat ditulis sebagai sebuah sistem

Memecahkan sistem ini sehubungan dengan B 1, kami memperoleh itu. Melakukan penalaran serupa untuk tangen l 3, mudah untuk menetapkan itu.

Mengganti nilai 1 dan B 1 ke dalam persamaan (1), kita memperoleh persamaan bidang singgung yang diperlukan:

Garis melalui titik M 0 dan tegak lurus terhadap bidang singgung yang dibangun pada titik permukaan ini disebut normal.

Menggunakan kondisi tegak lurus garis lurus dan bidang, mudah untuk mendapatkan persamaan kanonik normal:

Komentar. Rumus untuk bidang singgung dan normal ke permukaan diperoleh untuk biasa, yaitu, non-tunggal, titik permukaan. Titik M 0 permukaan disebut spesial, jika pada titik ini semua turunan parsial sama dengan nol atau setidaknya salah satunya tidak ada. Kami tidak mempertimbangkan poin seperti itu.

Contoh. Tuliskan persamaan bidang singgung dan garis normal permukaan pada titiknya M (2; -1; 1).

Larutan. Mari kita cari turunan parsial dari fungsi ini dan nilainya di titik M

Oleh karena itu, dengan menerapkan rumus (2) dan (3), kita akan mendapatkan: z-1 = 2 (x-2) +2 (y + 1) atau 2x + 2y-z-1 = 0- persamaan bidang singgung dan - persamaan normal.

2 °. Persamaan bidang singgung dan normal untuk kasus definisi permukaan implisit.

Jika permukaan S diberikan oleh persamaan F (x; y;z)= 0, maka persamaan (2) dan (3), dengan mempertimbangkan fakta bahwa turunan parsial dapat ditemukan sebagai turunan dari fungsi implisit.

Biarkan kita memiliki permukaan yang diberikan oleh persamaan bentuk

Mari kita perkenalkan definisi berikut.

Definisi 1. Suatu garis lurus disebut menyinggung permukaan di suatu titik jika garis tersebut

menyinggung setiap kurva yang terletak di permukaan dan melewati suatu titik.

Karena jumlah tak hingga kurva berbeda yang terletak di permukaan melewati titik P, maka akan ada, secara umum, satu set garis singgung tak terbatas ke permukaan yang melewati titik ini.

Mari kita perkenalkan konsep titik tunggal dan titik biasa dari permukaan

Jika pada suatu titik ketiga turunannya sama dengan nol atau paling tidak salah satu dari turunan tersebut tidak ada, maka titik M disebut titik singular dari permukaan. Jika pada suatu titik ketiga turunan ada dan kontinu, dan paling sedikit salah satunya bukan nol, maka titik M disebut titik biasa pada permukaan.

Sekarang kita dapat menyatakan teorema berikut.

Dalil. Semua garis singgung pada permukaan tertentu (1) pada titik biasa P terletak pada bidang yang sama.

Bukti. Pertimbangkan pada permukaan beberapa garis L (Gbr. 206) melewati titik P tertentu dari permukaan. Biarkan kurva yang dipertimbangkan diberikan oleh persamaan parametrik

Garis singgung kurva akan menyinggung permukaan. Persamaan garis singgung ini berbentuk

Jika ekspresi (2) disubstitusikan ke persamaan (1), maka persamaan ini akan berubah menjadi identitas terhadap t, karena kurva (2) terletak di permukaan (1). Membedakannya dengan kita dapatkan

Proyeksi vektor ini bergantung pada - koordinat titik P; perhatikan bahwa karena titik P adalah biasa, proyeksi di titik P ini tidak hilang secara bersamaan dan oleh karena itu

bersinggungan dengan kurva yang melalui titik P dan terletak di permukaan. Proyeksi vektor ini dihitung berdasarkan persamaan (2) dengan nilai parameter t yang sesuai dengan titik P.

Kami menghitung produk skalar vektor N dan yang sama dengan jumlah produk proyeksi dengan nama yang sama:

Berdasarkan persamaan (3), ekspresi di ruas kanan sama dengan nol, oleh karena itu,

Dari persamaan terakhir diketahui bahwa vektor dan vektor tangen kurva (2) di titik tegak lurus. Alasan di atas berlaku untuk setiap kurva (2) yang melalui titik P dan terletak di permukaan. Akibatnya, setiap garis singgung permukaan di titik P tegak lurus terhadap vektor N yang sama, dan oleh karena itu semua garis singgung ini terletak pada bidang yang sama tegak lurus terhadap vektor . Teorema terbukti.

Definisi 2. Bidang di mana semua garis singgung ke garis pada permukaan melewati titik P tertentu berada disebut bidang singgung ke permukaan di titik P (Gbr. 207).

Perhatikan bahwa bidang singgung mungkin tidak ada pada titik tunggal permukaan. Pada titik-titik tersebut, garis singgung ke permukaan mungkin tidak terletak pada bidang yang sama. Jadi, misalnya, titik sudut permukaan runcing adalah titik tunggal.

Garis singgung permukaan kerucut pada titik ini tidak terletak pada bidang yang sama (mereka sendiri membentuk permukaan kerucut).

Mari kita tulis persamaan bidang singgung permukaan (1) di titik biasa. Karena bidang ini tegak lurus terhadap vektor (4), maka persamaannya berbentuk

Jika persamaan permukaan diberikan dalam bentuk atau persamaan bidang singgung dalam hal ini mengambil bentuk

Komentar. Jika kita masukkan ke dalam rumus (6), maka rumus ini berbentuk

sisi kanannya mewakili diferensial penuh dari fungsi tersebut. Karenanya, . Jadi, diferensial total fungsi dua variabel pada titik yang bersesuaian dengan kenaikan variabel bebas x dan y sama dengan kenaikan yang sesuai dari penerapan bidang singgung ke permukaan, yang merupakan grafik fungsi ini.

Definisi 3. Garis lurus yang ditarik melalui suatu titik pada permukaan (1) yang tegak lurus terhadap bidang singgung disebut garis normal permukaan (Gbr. 207).

Mari kita menulis persamaan untuk normal. Karena arahnya bertepatan dengan arah vektor N, persamaannya akan berbentuk

Unduh dari Depositfiles

4. TEORI PERMUKAAN.

4.1 PERSAMAAN UNTUK PERMUKAAN.

Permukaan dalam ruang 3D dapat ditentukan:

1) secara implisit: F ( x , kamu , z ) =0 (4.1)

2) secara eksplisit: z = F ( x , kamu ) (4.2)

3) secara parametrik: (4.3)

atau:
(4.3’)

di mana argumen skalar
kadang-kadang disebut koordinat lengkung. Misalnya bola
lebih mudah untuk mengatur dalam koordinat bola:
.

4.2 BIDANG TANGEN DAN NORMAL KE PERMUKAAN.

Jika garis terletak pada permukaan (4.1), maka koordinat titik-titiknya memenuhi persamaan permukaan:

Membedakan identitas ini, kita mendapatkan:

(4.4)

atau
(4.4 ’ )

pada setiap titik kurva di permukaan. Jadi, vektor gradien pada titik nonsingular dari permukaan (di mana fungsi (4,5) dapat diturunkan dan
) tegak lurus terhadap vektor tangen terhadap sembarang garis pada permukaan, yaitu dapat digunakan sebagai vektor normal untuk menyusun persamaan bidang singgung di titik M 0 (x 0 , kamu 0 , z 0 ) permukaan

(4.6)

dan sebagai vektor arah dalam persamaan normal:

(4.7)

Dalam kasus eksplisit (4.2) menentukan permukaan, persamaan bidang singgung dan normal, masing-masing, mengambil bentuk:

(4.8)

dan
(4.9)

Dalam representasi parametrik dari permukaan (4.3), vektor
terletak pada bidang singgung dan persamaan bidang singgung dapat ditulis sebagai:

(4.10)

dan hasil kali silangnya dapat diambil sebagai vektor arah dari normal:

dan persamaan normalnya dapat ditulis sebagai:

(4.11)

di mana
- nilai parameter sesuai dengan titik 0 .

Berikut ini, kami membatasi diri untuk hanya mempertimbangkan titik-titik permukaan di mana vektor

tidak sama dengan nol dan tidak sejajar.

Contoh 4.1 Buatlah persamaan bidang singgung dan garis normal di titik M 0 (1,1,2) ke permukaan paraboloid revolusi
.

Solusi: Karena persamaan paraboloid diberikan secara eksplisit, menurut (4.8) dan (4.9), Anda perlu mencari
di titik M 0 :

, dan pada titik 0
... Maka persamaan bidang singgung di titik M 0 akan berbentuk:

2(x -1)+2(kamu -1)-(z-2) = 0 atau 2 x +2 kamu - z - 2 = 0, dan persamaan normal
.

Contoh 4.2 Tuliskan persamaan bidang singgung dan normal pada titik sembarang helikoid
, .

Larutan. Di Sini ,

Persamaan bidang singgung:

atau

Persamaan normal:

.

4.3 BENTUK PERMUKAAN KOTAK PERTAMA.

Jika permukaan diberikan oleh persamaan

maka kurva
di atasnya dapat diberikan oleh persamaan
(4.12)

Diferensial vektor radius
sepanjang kurva yang sesuai dengan perpindahan dari titik M 0 ke titik terdekat M sama dengan

(4.13)

Karena
Apakah diferensial busur kurva sesuai dengan perpindahan yang sama), maka

(4.14)

di mana .

Ekspresi di sisi kanan (4.14) disebut bentuk permukaan kuadrat pertama dan memainkan peran besar dalam teori permukaan.

Saya mengintegrasikan diferensialds mulai dari T 0 (sesuai dengan poin 0) ke t (sesuai dengan titik M), kami memperoleh panjang segmen kurva yang sesuai

(4.15)

Mengetahui bentuk kuadrat pertama dari permukaan, Anda tidak hanya dapat menemukan panjangnya, tetapi juga sudut di antara kurva.

Jika du , dv Apakah perbedaan koordinat lengkung sesuai dengan perpindahan sangat kecil sepanjang satu kurva, dan
- di sisi lain, kemudian, dengan mempertimbangkan (4.13):

(4.16)

Menggunakan rumus

(4.17)

bentuk kuadrat pertama memungkinkan untuk menghitung luas wilayah
permukaan.

Contoh 4.3 Pada helikoid, temukan panjang heliks
antara dua titik.

Larutan. Sejak di heliks
, kemudian . Temukan pada intinya
bentuk kuadrat pertama. Menunjukkan danv = T , kita mendapatkan persamaan garis heliks ini dalam bentuk. Bentuk kuadrat:

= Apakah bentuk kuadrat pertama.

Di Sini . Dalam rumus (4.15), dalam hal ini
dan panjang busur:

=

4.4 BENTUK PERMUKAAN PERSEGI KEDUA.

Kami menunjukkan
Apakah vektor normal satuan ke permukaan?
:

(4.18) . (4.23)

Garis pada suatu permukaan disebut garis kelengkungan jika arahnya pada setiap titik adalah arah utama.

4.6 KONSEP GARIS GEODETIK PERMUKAAN.

Definisi 4.1 ... Sebuah kurva pada permukaan disebut geodesik jika normal utamanya di setiap titik di mana kelengkungan berbeda dari nol bertepatan dengan normal ke permukaan.

Ini melewati setiap titik permukaan ke segala arah, dan terlebih lagi, hanya satu geodesik. Pada bola, misalnya, lingkaran besar adalah geodesik.

Parametrisasi suatu permukaan disebut semi-geodesik jika satu keluarga garis koordinat terdiri dari geodesik, dan yang kedua ortogonal terhadapnya. Misalnya pada bidang meridian (geodesik) dan paralel.

Geodesik pada segmen yang cukup kecil adalah yang terpendek di antara semua kurva yang dekat dengannya, menghubungkan titik-titik yang sama.

Yaitu, apa yang Anda lihat di judul. Pada dasarnya, ini adalah "analog spasial" masalah menemukan garis singgung dan normal ke grafik fungsi satu variabel, dan karena itu tidak ada kesulitan yang muncul.

Mari kita mulai dengan beberapa pertanyaan dasar: APA ITU bidang singgung dan APA ITU normal? Banyak yang menyadari konsep-konsep ini pada tingkat intuisi. Model paling sederhana yang terlintas dalam pikiran adalah bola dengan selembar karton tipis yang diletakkan di atasnya. Karton terletak sedekat mungkin dengan bola dan menyentuhnya pada satu titik. Selain itu, pada titik kontak, itu diperbaiki dengan jarum yang mencuat lurus ke atas.

Secara teori, ada definisi yang agak cerdik tentang bidang singgung. Bayangkan sewenang-wenang permukaan dan titik miliknya. Jelas, banyak garis spasial yang dimiliki permukaan ini. Siapa yang memiliki asosiasi apa? =) ... Saya pribadi memperkenalkan gurita. Misalkan setiap baris tersebut memiliki tangen spasial pada intinya.

Definisi 1: bidang singgung ke permukaan pada suatu titik adalah pesawat mengandung garis singgung semua kurva yang dimiliki permukaan ini dan melewati titik.

Definisi 2: normal ke permukaan pada suatu titik adalah lurus melewati titik ini tegak lurus terhadap bidang singgung.

Sederhana dan elegan. Omong-omong, agar Anda tidak mati kebosanan dari kesederhanaan materi, sedikit kemudian saya akan berbagi dengan Anda satu rahasia elegan yang memungkinkan SEKALI DAN SELAMANYA untuk melupakan menjejalkan berbagai definisi.

Kami akan berkenalan dengan rumus kerja dan algoritma solusi langsung pada contoh spesifik. Dalam sebagian besar masalah, diperlukan untuk menyusun persamaan bidang singgung dan persamaan normal:

Contoh 1

Larutan: jika permukaan diberikan oleh persamaan (yaitu secara implisit), maka persamaan bidang singgung ke permukaan tertentu di suatu titik dapat ditemukan dengan rumus berikut:

Saya memberikan perhatian khusus pada turunan parsial yang tidak biasa - mereka jangan bingung dengan turunan parsial dari fungsi yang didefinisikan secara implisit (meskipun permukaan secara implisit ditentukan)... Saat menemukan turunan ini, Anda perlu dipandu oleh aturan diferensiasi fungsi tiga variabel, yaitu, ketika membedakan sehubungan dengan variabel apa pun, dua huruf lainnya dianggap konstanta:

Tanpa meninggalkan kasir, kami menemukan turunan parsial pada titik:

Demikian pula:

Ini adalah momen keputusan yang paling tidak menyenangkan, di mana kesalahan, jika tidak diizinkan, terus-menerus muncul. Namun demikian, ada teknik verifikasi yang efektif di sini, yang saya bicarakan dalam pelajaran Turunan dan gradien terarah.

Semua "bahan" telah ditemukan, dan sekarang terserah pada penggantian yang rapi dengan penyederhanaan lebih lanjut:

– persamaan umum bidang singgung yang diinginkan.

Saya sangat menyarankan Anda memeriksa tahap solusi ini juga. Pertama, Anda perlu memastikan bahwa koordinat titik sentuh benar-benar memenuhi persamaan yang ditemukan:

- kesetaraan sejati.

Sekarang kita "menghilangkan" koefisien persamaan umum bidang dan memeriksanya untuk kebetulan atau proporsionalitas dengan nilai yang sesuai. Dalam hal ini, mereka proporsional. Apakah kamu ingat dari mata kuliah geometri analitik, - ini vektor normal bidang singgung, dan dia adalah - vektor arah garis lurus biasa. Mari menulis persamaan kanonik normal menurut vektor titik dan arah:

Pada prinsipnya, penyebut dapat dikurangi dengan "dua", tetapi tidak ada kebutuhan khusus untuk ini

Menjawab:

Tidak dilarang untuk menunjuk persamaan dengan beberapa huruf, namun, sekali lagi - mengapa? Di sini, dan sangat jelas apa apa.

Dua contoh berikutnya adalah untuk membantu diri sendiri. Sedikit "twister lidah matematika":

Contoh 2

Tentukan persamaan bidang singgung dan garis normal permukaan di suatu titik.

Dan tugas yang menarik dari sudut pandang teknis:

Contoh 3

Tuliskan persamaan bidang singgung dan garis normal permukaan di suatu titik

Pada intinya.

Ada setiap kesempatan tidak hanya untuk bingung, tetapi juga menghadapi kesulitan saat merekam persamaan kanonik garis... Dan persamaan normal, seperti yang mungkin Anda pahami, biasanya ditulis dalam bentuk ini. Meskipun, karena kelupaan atau ketidaktahuan beberapa nuansa, bentuk parametrik lebih dari dapat diterima.

Contoh contoh penyelesaian penyelesaian di akhir pelajaran.

Apakah ada bidang singgung di sembarang titik di permukaan? Secara umum, tentu saja tidak. Contoh klasik adalah permukaan meruncing dan titik - garis singgung pada titik ini secara langsung membentuk permukaan kerucut, dan, tentu saja, tidak terletak pada bidang yang sama. Sangat mudah untuk diyakinkan tentang masalah secara analitis:.

Sumber masalah lain adalah fakta ketiadaan setiap turunan parsial pada suatu titik. Namun, ini tidak berarti bahwa pada suatu titik tertentu tidak ada bidang singgung tunggal.

Tapi itu, lebih tepatnya, sains populer daripada informasi praktis yang signifikan, dan kami kembali ke masalah sehari-hari kami:

Bagaimana menulis persamaan bidang singgung dan normal di suatu titik,
jika permukaan diberikan oleh fungsi eksplisit?

Mari kita tulis ulang secara implisit:

Dan menurut prinsip yang sama, kita akan menemukan turunan parsial:

Dengan demikian, rumus bidang singgung diubah menjadi persamaan berikut:

Dan dengan demikian, persamaan normal kanonik:

Seperti yang Anda duga, - ini sudah "nyata" turunan parsial dari fungsi dua variabel pada titik yang kami gunakan untuk menunjuk dengan huruf "z" dan ditemukan 100.500 kali.

Perhatikan bahwa dalam artikel ini cukup untuk mengingat formula pertama, dari mana, jika perlu, mudah untuk mendapatkan yang lainnya. (dimengerti, memiliki tingkat pelatihan dasar)... Ini adalah pendekatan yang harus digunakan dalam studi ilmu-ilmu eksakta, yaitu. dari informasi minimum, seseorang harus berusaha untuk "menarik" kesimpulan dan konsekuensi maksimum. "Soobrazhalovka" dan pengetahuan yang sudah ada untuk membantu! Prinsip ini juga berguna karena kemungkinan besar akan menghemat dalam situasi kritis ketika Anda hanya tahu sedikit.

Mari kita kerjakan rumus yang "dimodifikasi" dengan beberapa contoh:

Contoh 4

Tulis persamaan untuk bidang singgung dan normal ke permukaan pada intinya.

Hamparan kecil di sini ternyata dengan sebutan - sekarang surat itu menunjukkan titik di pesawat, tetapi apa yang harus dilakukan - surat yang begitu populer….

Larutan: persamaan bidang singgung yang diperlukan disusun dengan rumus:

Mari kita hitung nilai fungsi di titik:

Mari kita hitung Turunan parsial orde pertama pada saat ini:

Dengan demikian:

hati-hati, tidak terburu-buru:

Kami menulis persamaan kanonik normal di titik:

Menjawab:

Dan contoh terakhir untuk solusi do-it-yourself:

Contoh 5

Tuliskan persamaan bidang singgung dan garis normal permukaan di suatu titik.

Yang terakhir - karena sebenarnya saya telah menjelaskan semua poin teknis dan tidak ada yang istimewa untuk ditambahkan. Bahkan fungsi itu sendiri, yang ditawarkan dalam tugas ini, membosankan dan monoton - hampir dijamin dalam praktiknya Anda akan menemukan "polinomial", dan dalam pengertian ini Contoh # 2 dengan eksponen terlihat seperti "kambing hitam". Omong-omong, itu lebih mungkin untuk memenuhi permukaan yang diberikan oleh persamaan, dan ini adalah alasan lain mengapa fungsi itu dimasukkan dalam artikel "angka kedua".

Dan akhirnya, rahasia yang dijanjikan: bagaimana Anda bisa menghindari definisi yang menjejalkan? (Saya, tentu saja, tidak bermaksud situasi di mana seorang siswa dengan panik menjejalkan sesuatu sebelum ujian)

Definisi konsep / fenomena / objek apa pun, pertama-tama, memberikan jawaban atas pertanyaan berikut: APA ITU? (siapa / seperti / itu / itu). Secara sadar dalam menjawab pertanyaan ini, Anda harus mencoba untuk merenungkan penting tanda-tanda, dengan tegas mengidentifikasi konsep/fenomena/objek ini atau itu. Ya, pada awalnya ini ternyata agak kaku, tidak akurat dan berlebihan (guru akan mengoreksi =)), tetapi seiring waktu, pidato ilmiah yang benar-benar layak berkembang.

Berlatihlah pada objek yang paling abstrak, misalnya, jawab pertanyaan: siapa Cheburashka? Tidak sesederhana itu ;-) Apakah ini "karakter dongeng dengan telinga besar, mata dan rambut cokelat"? Jauh dan sangat jauh dari definisi - Anda tidak pernah tahu ada karakter dengan karakteristik seperti itu .... Tapi ini sudah jauh lebih dekat dengan definisi: "Cheburashka adalah karakter yang ditemukan oleh penulis Eduard Uspensky pada tahun 1966, yang ... (penjumlahan fitur pembeda utama)"... Perhatikan seberapa baik itu dimulai