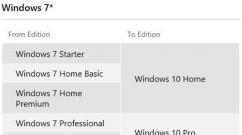
Contoh proyeksi titik. Memproyeksikan titik ke tiga bidang proyeksi. Persamaan garis lurus untuk ruang dua dimensi dan tiga dimensi

Sebuah titik, sebagai konsep matematika, tidak memiliki dimensi. Jelas, jika objek proyeksi adalah objek berdimensi nol, maka berbicara tentang proyeksinya tidak ada artinya.

Gambar.9 Gambar.10

Dalam geometri, di bawah suatu titik, disarankan untuk mengambil objek fisik dengan dimensi linier. Secara konvensional, bola dengan jari-jari yang sangat kecil dapat diambil sebagai titik. Dengan interpretasi konsep suatu titik seperti itu, seseorang dapat berbicara tentang proyeksinya.

Saat membuat proyeksi ortogonal suatu titik, seseorang harus dipandu oleh sifat invarian pertama dari proyeksi ortogonal: proyeksi ortogonal suatu titik adalah titik.

Posisi suatu titik dalam ruang ditentukan oleh tiga koordinat: X, Y, Z, menunjukkan nilai jarak di mana titik dihilangkan dari bidang proyeksi. Untuk menentukan jarak ini, cukup menentukan titik pertemuan garis lurus ini dengan bidang proyeksi dan mengukur nilai yang sesuai, yang masing-masing akan menunjukkan nilai absis. x, ordinat kamu dan aplikasi Z poin (gbr. 10).

Proyeksi suatu titik adalah alas garis tegak lurus yang dijatuhkan dari titik tersebut ke bidang proyeksi yang sesuai. Proyeksi horizontal poin sebuah disebut proyeksi persegi panjang dari suatu titik pada bidang proyeksi horizontal, proyeksi depan a /- masing-masing pada bidang depan proyeksi dan profil a // - pada bidang profil proyeksi.

Langsung Aa, Aa / dan A A // disebut garis proyeksi. Apalagi yang lurus A A, titik proyeksi SEBUAH pada bidang proyeksi horizontal, yang disebut horizontal memproyeksikan garis lurus, a / dan A A //- masing-masing: secara frontal dan garis lurus yang memproyeksikan profil.

Dua garis proyeksi yang melalui suatu titik SEBUAH mendefinisikan pesawat, yang biasanya disebut memproyeksikan.

Saat mengubah tata ruang, proyeksi depan titik A A / tetap di tempatnya, sebagai milik pesawat, yang tidak mengubah posisinya selama transformasi yang sedang dipertimbangkan. Proyeksi horisontal - sebuah bersama dengan bidang proyeksi horizontal akan berputar dengan arah gerak searah jarum jam dan akan berada pada satu tegak lurus sumbu x dengan proyeksi frontal. Proyeksi profil - sebuah // akan berputar bersama dengan bidang profil dan pada akhir transformasi akan mengambil posisi yang ditunjukkan pada Gambar 10. Dalam hal ini - sebuah // akan menjadi milik tegak lurus terhadap sumbu Z ditarik dari titik sebuah / dan akan dihapus dari sumbu Z jarak yang sama dengan proyeksi horizontal sebuah dihapus dari sumbu x... Oleh karena itu, hubungan antara proyeksi horizontal dan profil suatu titik dapat dibuat dengan menggunakan dua segmen ortogonal aa y dan a y a // dan busur lingkaran yang menghubungkannya dengan pusat di titik perpotongan sumbu ( HAI- asal). Sambungan yang ditandai digunakan untuk menemukan proyeksi yang hilang (untuk dua yang diberikan). Posisi proyeksi profil (horizontal) menurut proyeksi horizontal (profil) dan frontal yang diberikan dapat ditemukan dengan menggunakan garis lurus yang ditarik pada sudut 45 0 dari asal ke sumbu kamu(pembagi ini disebut garis lurus k- konstanta Monge). Yang pertama dari metode ini lebih disukai karena lebih akurat.

Karena itu:

1. Titik di ruang dihapus:

dari bidang horizontal H Z,

dari bidang frontal V dengan nilai koordinat yang diberikan y,

dari pesawat profil W dengan nilai koordinat. X.

2. Dua proyeksi dari sembarang titik memiliki tegak lurus yang sama (satu jalur komunikasi):

horizontal dan frontal - tegak lurus terhadap sumbu X,

horizontal dan profil - tegak lurus terhadap sumbu Y,

frontal dan profil - tegak lurus terhadap sumbu Z.

3. Posisi suatu titik dalam ruang ditentukan sepenuhnya oleh posisi kedua proyeksi ortogonalnya. Karena itu - dua proyeksi ortogonal yang diberikan dari suatu titik selalu dapat digunakan untuk membangun proyeksi ketiga yang hilang.

Jika suatu titik memiliki tiga koordinat tertentu, maka titik tersebut disebut titik posisi umum. Jika suatu titik memiliki satu atau dua koordinat nol, maka titik tersebut disebut titik posisi tertentu.

Beras. 11 Gambar. 12

Gambar 11 memberikan gambar spasial dari titik-titik posisi tertentu, Gambar 12 - gambar kompleks (diagram) dari titik-titik ini. Dot SEBUAH milik bidang proyeksi frontal, titik V- bidang proyeksi horizontal, titik DENGAN- bidang profil proyeksi dan titik D- sumbu absis ( x).

Peralatan proyeksi

Perangkat proyeksi (Gbr. 1) mencakup tiga bidang proyeksi:

1 - bidang proyeksi horizontal;

2 - bidang proyeksi frontal;

3- bidang profil proyeksi .

Bidang proyeksi terletak saling tegak lurus ( 1^ 2^ 3), dan garis perpotongannya membentuk sumbu:

Persimpangan pesawat 1 dan 2 membentuk sumbu 0X (1∩ 2 = 0X);

Persimpangan pesawat 1 dan 3 membentuk sumbu 0Y (1∩ 3 = 0Y);

Persimpangan pesawat 2 dan 3 membentuk sumbu 0Z (2∩ 3 = 0Z).

Titik perpotongan sumbu (ОХ∩OY∩OZ = 0) dianggap sebagai titik asal (titik 0).

Karena bidang dan sumbu saling tegak lurus, peralatan ini mirip dengan sistem koordinat Cartesian.

Bidang proyeksi dibagi menjadi delapan oktan (pada Gambar 1 mereka ditunjuk oleh angka Romawi). Bidang proyeksi dianggap buram, dan pemirsa selalu dalam Saya- oktan.

Proyeksi ortogonal dengan pusat proyeksi S 1, S 2 dan S 3 masing-masing untuk bidang proyeksi horizontal, frontal dan profil.

SEBUAH.

Dari pusat proyeksi S 1, S 2 dan S 3 balok proyeksi keluar l 1, l 2 dan l 3 SEBUAH

- 1 SEBUAH;

- A 2- proyeksi frontal suatu titik SEBUAH;

- A 3- proyeksi profil titik SEBUAH.

Suatu titik dalam ruang dicirikan oleh koordinatnya SEBUAH(x, y, z). Poin Sebuah x, Ay dan A z masing-masing pada sumbu 0X, 0Y dan 0Z menunjukkan koordinat x, y dan z poin SEBUAH... dalam gambar. 1 memberikan semua sebutan yang diperlukan dan menunjukkan hubungan antara titik SEBUAH ruang, proyeksi dan koordinatnya.

plot titik

Untuk mendapatkan plot titik SEBUAH(Gbr. 2), dalam peralatan proyeksi (Gbr. 1) bidang 1 1 0X 2... Kemudian pesawat 3 dengan proyeksi titik A 3, putar berlawanan arah jarum jam di sekitar sumbu 0Z, sebelum menyelaraskannya dengan pesawat 2... Arah rotasi pesawat 2 dan 3 ditunjukkan pada gambar. 1 dengan panah. Apalagi langsung A 1 A x dan A 2 A x 0X tegak lurus A 1 A 2 dan lurus A 2 A x dan A 3 A x akan ditempatkan pada sumbu yang sama 0Z tegak lurus A2A3... Berikut ini, garis-garis ini akan disebut, masing-masing. vertikal dan horisontal garis penghubung.

Perlu dicatat bahwa dalam transisi dari peralatan proyeksi ke diagram, objek yang diproyeksikan menghilang, tetapi semua informasi tentang bentuknya, dimensi geometris, dan posisinya dalam ruang dipertahankan.

SEBUAH(x A, y A, z Ax A, y A dan z A dalam urutan berikut (Gbr. 2). Urutan ini disebut teknik plotting titik.

1. Sumbu digambar secara ortogonal OK, OY dan ONS.

2. Pada porosnya SAPI x A poin SEBUAH dan dapatkan posisi poinnya Sebuah x.

3. Melalui titik Sebuah x tegak lurus sumbu SAPI

Sebuah x dalam arah sumbu OY nilai numerik koordinat ditunda y A poin SEBUAH 1 pada diagram.

Sebuah x dalam arah sumbu ONS nilai numerik koordinat ditunda z A poin SEBUAH A 2 pada diagram.

6. Melalui titik A 2 sejajar sumbu SAPI garis komunikasi horizontal ditarik. Perpotongan garis dan sumbu ini ONS akan memberikan posisi titik A z.

7. Pada jalur komunikasi horizontal dari titik A z dalam arah sumbu OY nilai numerik koordinat ditunda y A poin SEBUAH dan posisi proyeksi profil titik ditentukan A 3 pada diagram.

Karakteristik titik

Semua titik dalam ruang dibagi lagi menjadi titik-titik ketentuan khusus dan umum.

Poin posisi pribadi. Titik-titik yang dimiliki mesin proyeksi disebut titik posisi pribadi. Ini termasuk titik-titik milik bidang proyeksi, sumbu, asal, dan pusat proyeksi. Ciri-ciri ciri titik-titik pada posisi tertentu adalah:

Metamathematical - satu, dua atau semua nilai numerik dari koordinat sama dengan nol dan (atau) tak terhingga;

Di plot - dua atau semua proyeksi suatu titik terletak pada sumbu dan (atau) terletak di tak terhingga.

Poin posisi umum. Titik-titik posisi umum adalah titik-titik yang tidak termasuk dalam peralatan proyeksi. Misalnya, titik SEBUAH dalam gambar. 1 dan 2.

Dalam kasus umum, nilai numerik dari koordinat suatu titik mencirikan jaraknya dari bidang proyeksi: koordinat x dari pesawat 3; koordinat kamu dari pesawat 2; koordinat z dari pesawat 1... Perlu dicatat bahwa tanda-tanda pada nilai numerik koordinat menunjukkan arah di mana titik tersebut dihilangkan dari bidang proyeksi. Bergantung pada kombinasi tanda-tanda pada nilai numerik dari koordinat suatu titik, itu tergantung di mana oktan itu berada.

Metode dua gambar

Dalam praktiknya, selain metode proyeksi penuh, digunakan metode dua gambar. Ini berbeda karena metode ini mengecualikan proyeksi ketiga objek. Untuk mendapatkan peralatan proyeksi menggunakan metode dua gambar, bidang proyeksi profil dengan pusat proyeksinya dikeluarkan dari peralatan proyeksi penuh (Gbr. 3). Selain itu, pada poros 0X asal ditetapkan (titik 0 ) dan dari itu tegak lurus terhadap sumbu 0X di bidang proyeksi 1 dan 2 menggambar kapak 0Y dan 0Z masing-masing.

Dalam peralatan ini, seluruh ruang dibagi menjadi empat kuadran. dalam gambar. 3 mereka ditunjuk oleh angka Romawi.

Bidang proyeksi dianggap buram, dan pemirsa selalu dalam Saya kuadran ke-th.

Mari kita pertimbangkan pengoperasian perangkat menggunakan contoh proyeksi suatu titik SEBUAH.

Dari pusat proyeksi S 1 dan S 2 balok proyeksi keluar l 1 dan l 2... Sinar ini melewati titik SEBUAH dan berpotongan dengan bidang proyeksi membentuk proyeksinya:

- 1- proyeksi horizontal suatu titik SEBUAH;

- A 2- proyeksi frontal suatu titik SEBUAH.

Untuk mendapatkan plot titik SEBUAH(Gbr. 4), dalam peralatan proyeksi (Gbr. 3) bidang 1 dengan proyeksi titik yang diperoleh 1 putar searah jarum jam di sekitar sumbu 0X, sebelum menyelaraskannya dengan pesawat 2... Arah rotasi pesawat 1 ditunjukkan pada gambar. 3 anak panah. Dalam hal ini, pada plot titik yang diperoleh dengan metode dua gambar, hanya satu yang tersisa vertikal jalur komunikasi A 1 A 2.

Dalam praktiknya, merencanakan sebuah titik SEBUAH(x A, y A, z A) dilakukan sesuai dengan nilai numerik koordinatnya x A, y A dan z A dalam urutan berikut (gbr. 4).

1. Sebuah sumbu ditarik SAPI dan asal ditetapkan (titik 0 ).

2. Pada porosnya SAPI nilai numerik koordinat ditunda x A poin SEBUAH dan dapatkan posisi poinnya Sebuah x.

3. Melalui titik Sebuah x tegak lurus sumbu SAPI garis komunikasi vertikal sedang ditarik.

4. Pada jalur komunikasi vertikal dari titik Sebuah x dalam arah sumbu OY nilai numerik koordinat ditunda y A poin SEBUAH dan posisi proyeksi horizontal titik ditentukan 1 OY tidak diplot, tetapi diasumsikan bahwa nilai positifnya terletak di bawah sumbu SAPI dan yang negatif lebih tinggi.

5. Pada jalur komunikasi vertikal dari titik Sebuah x dalam arah sumbu ONS nilai numerik koordinat ditunda z A poin SEBUAH dan posisi proyeksi frontal titik ditentukan A 2 pada diagram. Perlu dicatat bahwa pada diagram sumbu ONS tidak diplot, tetapi diasumsikan bahwa nilai positifnya terletak di atas sumbu SAPI dan yang negatif lebih rendah.

Poin kompetisi

Titik pada satu sinar proyeksi disebut titik bersaing. Mereka memiliki proyeksi yang sama ke arah sinar proyeksi, mis. proyeksi mereka identik. Ciri khas dari titik-titik yang bersaing di plot adalah kebetulan yang identik dari proyeksi mereka dengan nama yang sama. Persaingan terletak pada visibilitas proyeksi ini relatif terhadap pengamat. Dengan kata lain, di ruang angkasa bagi pengamat salah satu titik terlihat, yang lain tidak. Dan, karenanya, dalam gambar: salah satu proyeksi titik yang bersaing terlihat, dan proyeksi titik lainnya tidak terlihat.

Pada model proyeksi spasial (Gbr. 5) dari dua titik yang bersaing SEBUAH dan V titik terlihat SEBUAH menurut dua sifat yang saling melengkapi. Dilihat dari rantainya S 1 → A → B dot SEBUAH lebih dekat ke pengamat daripada titik V... Dan, karenanya, - lebih jauh dari bidang proyeksi 1(itu. z A > z A).

Beras. Gambar 6

Jika titik itu sendiri terlihat SEBUAH, maka proyeksinya juga terlihat 1... Sehubungan dengan proyeksi yang bertepatan dengan itu B1... Untuk kejelasan dan, jika perlu, pada diagram, proyeksi titik yang tidak terlihat biasanya diapit dalam tanda kurung.

Mari kita hilangkan poin pada model SEBUAH dan V... Proyeksi mereka yang bertepatan di pesawat akan tetap ada 1 dan proyeksi terpisah - aktif 2... Mari kita tinggalkan proyeksi frontal pengamat (⇩) yang terletak di tengah proyeksi S 1... Kemudian sepanjang rantai gambar → A 2 → B2 itu akan mungkin untuk menilai itu z A > z B dan titik itu sendiri terlihat SEBUAH dan proyeksinya 1.

Pertimbangkan poin yang bersaing dengan cara yang sama DENGAN dan D tampaknya relatif terhadap bidang 2. Karena sinar proyeksi umum dari titik-titik ini l 2 sejajar sumbu 0Y, maka tanda visibilitas poin bersaing DENGAN dan D ditentukan oleh pertidaksamaan y C> y D... Oleh karena itu, intinya D ditutup dengan titik DENGAN dan, karenanya, proyeksi titik D 2 akan dicakup oleh proyeksi titik C2 di permukaan 2.

Pertimbangkan bagaimana visibilitas titik bersaing dalam gambar komposit ditentukan (Gambar 6).

Berdasarkan proyeksi kebetulan 1≡DALAM 1 poinnya sendiri SEBUAH dan V berada pada satu sinar proyeksi sejajar sumbu 0Z... Ini berarti bahwa koordinat dapat dibandingkan z A dan z B titik-titik ini. Untuk ini, kami menggunakan bidang proyeksi frontal dengan gambar titik terpisah. Pada kasus ini z A > z B... Dari sini dapat disimpulkan bahwa proyeksi yang terlihat 1.

Poin C dan D dalam gambar kompleks yang dipertimbangkan (Gbr. 6) juga terletak pada satu sinar proyeksi, tetapi hanya sejajar dengan sumbu 0Y... Oleh karena itu, dari perbandingan y C> y D kami menyimpulkan bahwa proyeksi C 2 terlihat.

Peraturan umum. Visibilitas untuk proyeksi bertepatan titik bersaing ditentukan dengan membandingkan koordinat titik-titik ini ke arah sinar proyeksi umum. Proyeksi titik di mana koordinat ini lebih besar terlihat. Dalam hal ini, perbandingan koordinat dilakukan pada bidang proyeksi dengan gambar titik yang terpisah.

Pertimbangkan proyeksi titik pada dua bidang, di mana kami mengambil dua bidang tegak lurus (Gbr. 4), yang akan kami sebut bidang dan bidang frontal horizontal. Garis perpotongan bidang-bidang ini disebut sumbu proyeksi. Pada bidang yang dipertimbangkan, kami memproyeksikan satu titik A menggunakan proyeksi bidang. Untuk melakukan ini, perlu untuk menurunkan tegak lurus Aa dan A dari titik ini ke bidang yang dipertimbangkan.

Proyeksi pada bidang mendatar disebut proyeksi horizontal poin SEBUAH dan proyeksi sebuah? pada bidang frontal disebut proyeksi depan.

Titik-titik yang akan diproyeksikan biasanya dilambangkan dalam geometri deskriptif dengan menggunakan huruf latin yang besar. A, B, C... Huruf kecil digunakan untuk menunjukkan proyeksi horizontal titik. a, b, c... Proyeksi frontal ditunjukkan dengan huruf kecil dengan goresan di bagian atas a?, b?, c?…

Penunjukan titik dengan angka Romawi I, II, ... juga digunakan, dan untuk proyeksinya - dengan angka Arab 1, 2 ... dan 1 ?, 2? ...

Saat Anda memutar bidang horizontal sebesar 90 °, Anda bisa mendapatkan gambar di mana kedua bidang berada pada bidang yang sama (Gbr. 5). Gambar ini disebut plot titik.

Melalui garis tegak lurus A A dan Hah? menggambar sebuah pesawat (Gbr. 4). Bidang yang dihasilkan tegak lurus terhadap bidang frontal dan horizontal, karena mengandung tegak lurus terhadap bidang-bidang tersebut. Oleh karena itu, bidang ini tegak lurus terhadap garis perpotongan bidang-bidang tersebut. Garis lurus yang dihasilkan memotong bidang horizontal dalam garis lurus A A x, dan bidang frontal - dalam garis lurus hah? X. Lurus aah dan hah? x tegak lurus terhadap sumbu perpotongan bidang. Itu adalah Aaah? adalah persegi panjang.

Saat menggabungkan bidang proyeksi horizontal dan frontal sebuah dan sebuah? akan terletak pada tegak lurus yang sama terhadap sumbu perpotongan bidang, karena ketika bidang horizontal berputar, tegak lurus segmen A A x dan hah? x tidak akan dilanggar.

Kami mendapatkannya di diagram proyeksi sebuah dan sebuah? beberapa titik SEBUAH selalu terletak pada tegak lurus yang sama terhadap sumbu perpotongan bidang.

Dua proyeksi a dan sebuah? beberapa titik A dapat secara unik menentukan posisinya dalam ruang (Gbr. 4). Hal ini ditegaskan oleh fakta bahwa ketika membangun tegak lurus dari proyeksi a ke bidang horizontal, itu akan melewati titik A. Dengan cara yang sama, tegak lurus dari proyeksi sebuah? ke bidang frontal akan melewati titik SEBUAH, yaitu titik SEBUAH terletak bersamaan pada dua garis tertentu. Titik A adalah titik potongnya, yaitu pasti.

Perhatikan persegi panjang aaa x sebuah?(Gbr. 5), yang pernyataan berikut ini benar:

1) Jarak titik SEBUAH dari bidang frontal sama dengan jarak proyeksi horizontal a dari sumbu perpotongan bidang, mis.

Hah? = A A X;

2) jarak titik SEBUAH dari bidang proyeksi horizontal sama dengan jarak proyeksi frontalnya sebuah? dari sumbu perpotongan bidang, mis.

A A = hah? X.

Dengan kata lain, bahkan tanpa titik itu sendiri pada plot, dengan hanya menggunakan dua proyeksinya, Anda dapat mengetahui berapa jarak dari masing-masing bidang proyeksi suatu titik tertentu.

Perpotongan dua bidang proyeksi membagi ruang menjadi empat bagian, yang disebut perempat(gbr. 6).

Sumbu perpotongan bidang membagi bidang horizontal menjadi dua bagian - depan dan belakang, dan bidang depan - menjadi bagian atas dan bawah. Bagian atas bidang frontal dan bagian depan bidang horizontal dianggap sebagai batas-batas kuartal pertama.

Saat menerima diagram, bidang horizontal berputar dan sejajar dengan bidang frontal (Gbr. 7). Dalam hal ini, bagian depan bidang horizontal akan bertepatan dengan bagian bawah bidang frontal, dan bagian belakang bidang horizontal - dengan bagian atas bidang frontal.

Gambar 8-11 menunjukkan titik A, B, C, D yang terletak di tempat yang berbeda. Titik A terletak di kuarter pertama, titik B di kuarter kedua, titik C di kuarter ketiga, dan titik D di kuarter keempat.

Ketika poin terletak di kuarter pertama atau keempat, mereka proyeksi horizontal berada di depan bidang horizontal, dan di plot mereka akan terletak di bawah sumbu perpotongan bidang. Ketika sebuah titik terletak di kuartal kedua atau ketiga, proyeksi horizontalnya akan terletak di belakang bidang horizontal, dan pada plot itu akan berada di atas sumbu perpotongan bidang.

Proyeksi frontal titik-titik yang terletak di kuarter pertama atau kedua akan terletak di bagian atas bidang frontal, dan pada plot akan berada di atas sumbu perpotongan bidang. Ketika sebuah titik terletak di kuartal ketiga atau keempat, proyeksi frontalnya berada di bawah sumbu perpotongan bidang.

Paling sering, dalam konstruksi nyata, sosok itu ditempatkan di kuartal pertama ruang.

Dalam beberapa kasus khusus, titik ( E) dapat terletak pada bidang horizontal (Gbr. 12). Dalam hal ini, proyeksi horizontal e dan titik itu sendiri akan bertepatan. Proyeksi frontal dari titik tersebut akan ditempatkan pada sumbu perpotongan bidang.

Dalam kasus ketika titik KE terletak di bidang frontal (Gbr. 13), proyeksi horizontalnya k terletak pada sumbu perpotongan bidang, dan frontal k? menunjukkan lokasi sebenarnya dari titik ini.

Untuk titik-titik tersebut, tanda bahwa ia terletak pada salah satu bidang proyeksi adalah bahwa salah satu proyeksinya berada pada sumbu perpotongan bidang-bidang tersebut.

Jika sebuah titik terletak pada sumbu perpotongan bidang proyeksi, titik itu dan kedua proyeksinya bertepatan.

Jika suatu titik tidak terletak pada bidang proyeksi, maka disebut titik posisi umum... Berikut ini, jika tidak ada tanda khusus, titik yang dipertimbangkan adalah titik pada posisi umum.

2. Kurangnya sumbu proyeksi

Untuk memperjelas penerimaan proyeksi suatu titik pada model yang tegak lurus terhadap bidang proyeksi (Gbr. 4), perlu mengambil selembar kertas tebal dalam bentuk persegi panjang memanjang. Itu perlu ditekuk di antara proyeksi. Garis lipatan akan mewakili sumbu perpotongan bidang. Jika, setelah itu, selembar kertas yang dilipat diluruskan lagi, kita mendapatkan diagram yang mirip dengan yang ditunjukkan pada gambar.

Menggabungkan dua bidang proyeksi dengan bidang gambar, Anda tidak dapat menunjukkan garis lipatan, yaitu, jangan menggambar sumbu perpotongan bidang pada plot.

Saat membangun di plot, proyeksi harus selalu ditempatkan sebuah dan sebuah? titik A pada satu garis vertikal (Gbr. 14), yang tegak lurus terhadap sumbu perpotongan bidang. Oleh karena itu, bahkan jika posisi sumbu perpotongan bidang tetap tidak ditentukan, tetapi arahnya ditentukan, sumbu perpotongan bidang dapat berada di plot hanya tegak lurus terhadap garis lurus. ah?.

Jika tidak ada sumbu proyeksi pada plot suatu titik, seperti pada gambar pertama 14 a, Anda dapat menyatakan posisi titik ini dalam ruang. Untuk melakukan ini, gambarlah di mana saja tegak lurus terhadap garis lurus ah? sumbu proyeksi, seperti pada gambar kedua (Gbr. 14) dan tekuk gambar di sepanjang sumbu ini. Jika kita mengembalikan tegak lurus pada titik-titik sebuah dan sebuah? sebelum mereka berpotongan, Anda bisa mendapatkan poin SEBUAH... Ketika Anda mengubah posisi sumbu proyeksi, posisi yang berbeda dari suatu titik relatif terhadap bidang proyeksi diperoleh, tetapi ketidakpastian posisi sumbu proyeksi tidak mempengaruhi posisi relatif beberapa titik atau angka dalam ruang.

3. Proyeksi suatu titik ke tiga bidang proyeksi

Pertimbangkan bidang profil proyeksi. Proyeksi pada dua bidang tegak lurus biasanya menentukan posisi gambar dan memungkinkan untuk mengetahui ukuran dan bentuk sebenarnya. Tetapi ada kalanya dua proyeksi tidak cukup. Kemudian konstruksi proyeksi ketiga diterapkan.

Bidang proyeksi ketiga digambar sehingga tegak lurus terhadap kedua bidang proyeksi secara bersamaan (Gbr. 15). Bidang ketiga biasanya disebut Profil.

Dalam konstruksi seperti itu, garis lurus yang sama dari bidang horizontal dan frontal disebut sumbu x , garis lurus bersama bidang horizontal dan bidang profil - sumbu pada , dan garis lurus yang sama dari bidang frontal dan profil adalah sumbu z ... Dot HAI yang dimiliki oleh ketiga bidang tersebut disebut origin.

Gambar 15a menunjukkan intinya SEBUAH dan tiga proyeksinya. Proyeksi ke bidang profil ( sebuah??) disebut proyeksi profil dan menunjukkan sebuah??.

Untuk mendapatkan plot titik A, yang terdiri dari tiga proyeksi sebuah, sebuah, perlu untuk memotong trihedron yang dibentuk oleh semua bidang di sepanjang sumbu y (Gbr. 15b) dan menggabungkan semua bidang ini dengan bidang proyeksi frontal. Bidang horizontal harus diputar terhadap sumbu x, dan bidang profilnya terhadap sumbu z dalam arah yang ditunjukkan oleh panah pada Gambar 15.

Gambar 16 menunjukkan posisi proyeksi Hah? dan sebuah?? poin SEBUAH, yang dihasilkan dari keselarasan ketiga bidang dengan bidang gambar.

Akibat pemotongan tersebut, sumbu y terjadi pada diagram di dua tempat yang berbeda. Pada bidang horizontal (Gbr. 16), dibutuhkan posisi vertikal (tegak lurus terhadap sumbu x), dan pada bidang profil - horizontal (tegak lurus terhadap sumbu z).

Gambar 16 menunjukkan tiga proyeksi Hah? dan sebuah?? poin A memiliki posisi yang ditentukan secara ketat pada diagram dan tunduk pada kondisi yang jelas:

sebuah dan sebuah? harus selalu terletak pada garis vertikal yang sama tegak lurus terhadap sumbu x;

sebuah? dan sebuah?? harus selalu berada pada garis horizontal yang sama tegak lurus terhadap sumbu z;

3) saat menggambar melalui proyeksi horizontal dan garis horizontal, dan melalui proyeksi profil sebuah??- garis lurus vertikal, garis lurus yang dibangun harus berpotongan pada garis-bagi sudut antara sumbu proyeksi, karena gambar Oa pada sebuah 0 sebuah n - persegi.

Saat melakukan konstruksi tiga proyeksi titik, perlu untuk memeriksa pemenuhan ketiga kondisi untuk setiap titik.

4. Koordinat titik

Posisi suatu titik dalam ruang dapat ditentukan dengan menggunakan tiga bilangan yang disebut koordinat... Setiap koordinat sesuai dengan jarak suatu titik dari beberapa bidang proyeksi.

Jarak titik yang ditentukan SEBUAH ke bidang profil adalah koordinat x, di mana x = Hah?(Gbr. 15), jarak ke bidang frontal adalah koordinat y, dan y = Hah?, dan jarak ke bidang horizontal adalah koordinat z, di mana z = A A.

Pada Gambar 15, titik A menempati lebar persegi panjang parallelepiped, dan pengukuran parallelepiped ini sesuai dengan koordinat titik ini, yaitu, masing-masing koordinat ditunjukkan pada Gambar 15 empat kali, yaitu:

x = a?A = Oa x = a y a = a z a ?;

y = a?A = Oa y = a x a = a z a ?;

z = aA = Oa z = a x a? = a y a ?.

Pada diagram (Gbr. 16), koordinat x dan z muncul tiga kali:

x = a z a? = Oa x = a y a,

z = axa? = Oa z = a y a ?.

Semua segmen yang sesuai dengan koordinat x(atau z) sejajar satu sama lain. Koordinat pada diwakili dua kali oleh sumbu vertikal:

y = Oa y = a x a

dan dua kali - terletak secara horizontal:

y = Oa y = a z a ?.

Perbedaan ini muncul karena fakta bahwa sumbu y hadir pada plot di dua posisi yang berbeda.

Perlu diperhatikan bahwa posisi setiap proyeksi ditentukan pada diagram hanya dengan dua koordinat, yaitu:

1) horisontal - koordinat x dan pada,

2) frontal - koordinat x dan z,

3) profil - koordinat pada dan z.

Menggunakan koordinat x, y dan z, Anda dapat membuat proyeksi suatu titik di plot.

Jika titik A ditentukan oleh koordinat, catatannya ditentukan sebagai berikut: A ( X; y; z).

Saat membuat proyeksi titik SEBUAH Anda perlu memeriksa pemenuhan kondisi berikut:

1) proyeksi horizontal dan frontal sebuah dan sebuah? x x;

2) proyeksi frontal dan profil sebuah? dan sebuah? harus terletak pada tegak lurus yang sama terhadap sumbu z karena mereka memiliki koordinat yang sama z;

3) proyeksi horizontal dan juga dihapus dari sumbu x seperti proyeksi profil sebuah dihapus dari sumbu z sejak proyeksi ah? dan ya? memiliki koordinat yang sama pada.

Jika suatu titik terletak pada salah satu bidang proyeksi, maka salah satu koordinatnya adalah nol.

Ketika sebuah titik terletak pada sumbu proyeksi, kedua koordinatnya adalah nol.

Jika sebuah titik terletak di titik asal, ketiga koordinatnya adalah nol.

Ketika memecahkan masalah geometris dalam ruang, masalah sering muncul dalam menentukan jarak antara bidang dan titik. Dalam beberapa kasus, ini diperlukan untuk solusi yang komprehensif. Nilai ini dapat dihitung dengan mencari proyeksi ke bidang titik. Mari kita pertimbangkan masalah ini secara lebih rinci di artikel.

Persamaan untuk menggambarkan sebuah pesawat

Sebelum melanjutkan untuk mempertimbangkan pertanyaan tentang bagaimana menemukan proyeksi suatu titik ke bidang, Anda harus berkenalan dengan jenis-jenis persamaan yang mendefinisikan yang terakhir dalam ruang tiga dimensi. Lebih detail di bawah ini.

Persamaan umum yang mendefinisikan semua titik yang termasuk dalam bidang tertentu adalah sebagai berikut:

A * x + B * y + C * z + D = 0.

Tiga koefisien pertama adalah koordinat vektor, yang disebut panduan untuk pesawat. Itu bertepatan dengan normal untuk itu, yaitu tegak lurus. Vektor ini dilambangkan dengan n¯ (A; B; C). Koefisien bebas D ditentukan secara unik dari pengetahuan tentang koordinat titik mana pun yang termasuk dalam bidang.

Konsep proyeksi suatu titik dan perhitungannya

Misalkan beberapa titik P (x 1; y 1; z 1) dan sebuah bidang diberikan. Ini didefinisikan oleh persamaan umum. Jika kita menggambar garis tegak lurus dari P ke bidang tertentu, maka jelas bahwa ia akan memotong yang terakhir di satu titik tertentu Q (x 2; y 2; z 2). Q disebut proyeksi P ke bidang yang bersangkutan. Panjang segmen PQ disebut jarak dari titik P ke bidang. Jadi, PQ sendiri tegak lurus bidang.

Bagaimana cara mencari koordinat proyeksi suatu titik pada bidang datar? Ini tidak sulit untuk dilakukan. Pertama, Anda perlu membuat persamaan untuk garis lurus yang tegak lurus terhadap bidang. Titik P akan menjadi miliknya Karena vektor normal n¯ (A; B; C) dari garis ini harus sejajar, persamaan untuk itu dalam bentuk yang sesuai akan ditulis sebagai berikut:

(x; y; z) = (x 1; y 1; z 1) + * (A; B; C).

Dimana adalah bilangan real, yang biasanya disebut parameter persamaan. Dengan mengubahnya, Anda bisa mendapatkan titik mana pun dari garis lurus.

Setelah persamaan vektor untuk garis tegak lurus bidang ditulis, perlu untuk menemukan titik potong bersama untuk objek geometris yang dipertimbangkan. Koordinatnya akan menjadi proyeksi P. Karena keduanya harus memenuhi kedua persamaan (untuk garis lurus dan bidang), masalahnya direduksi menjadi penyelesaian sistem persamaan linier yang sesuai.

Konsep proyeksi sering digunakan ketika mempelajari gambar. Mereka menggambarkan proyeksi samping dan horizontal bagian pada bidang zy, zx, dan xy.

Menghitung jarak dari bidang ke titik

Seperti disebutkan di atas, mengetahui koordinat proyeksi ke bidang suatu titik memungkinkan Anda menentukan jarak di antara mereka. Menggunakan notasi yang diperkenalkan pada bagian sebelumnya, kami menemukan bahwa jarak yang diperlukan sama dengan panjang segmen PQ. Untuk menghitungnya, cukup dengan menemukan koordinat vektor PQ¯, dan kemudian menghitung modulusnya menggunakan rumus yang terkenal. Ekspresi akhir untuk jarak d antara titik P dan bidang berbentuk:

d = | PQ¯ | = ((x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2).

Nilai d yang dihasilkan disajikan dalam satuan di mana sistem koordinat Cartesian saat ini xyz ditentukan.

Contoh tugas

Misalkan ada titik N (0; -2; 3) dan sebuah bidang, yang digambarkan dengan persamaan berikut:

Penting untuk menemukan titik-titik proyeksi ke pesawat dan menghitung jarak di antara mereka.

Pertama-tama, kita akan merumuskan persamaan garis lurus yang memotong bidang dengan sudut 90 o. Kita punya:

(x; y; z) = (0; -2; 3) + * (2; -1; 1).

Menulis persamaan ini secara eksplisit, kita sampai pada sistem persamaan berikut:

Mengganti nilai koordinat dari tiga persamaan pertama menjadi persamaan keempat, kami memperoleh nilai , yang menentukan koordinat titik bersama garis dan bidang:

2 * (2 * ) - (-2 - ) + + 3 + 4 = 0 =>

6 * + 9 = 0 =>

= 9/6 = 3/2 = 1,5.

Substitusikan parameter yang ditemukan di dan temukan koordinat proyeksi titik awal pada bidang:

(x; y; z) = (0; -2; 3) + 1,5 * (2; -1; 1) = (3; -3.5; 4.5).

Untuk menghitung jarak antara objek geometris yang ditentukan dalam pernyataan masalah, kami menerapkan rumus untuk d:

d = ((3 - 0) 2 + (-3.5 + 2) 2 + (4,5 - 3) 2) = 3,674.

Dalam tugas ini, kami menunjukkan cara menemukan proyeksi suatu titik pada bidang sembarang dan cara menghitung jarak di antara keduanya.

Studi tentang sifat-sifat bangun di ruang dan di pesawat tidak mungkin tanpa mengetahui jarak antara titik dan objek geometris seperti garis lurus dan bidang. Pada artikel ini, kami akan menunjukkan cara menemukan jarak ini, dengan mempertimbangkan proyeksi suatu titik pada bidang dan garis lurus.

Persamaan garis lurus untuk ruang dua dimensi dan tiga dimensi

Perhitungan jarak suatu titik ke garis lurus dan bidang dilakukan dengan menggunakan proyeksinya ke benda-benda ini. Untuk dapat menemukan proyeksi ini, Anda harus mengetahui dalam bentuk apa persamaan garis dan bidang diberikan. Mari kita mulai dengan yang pertama.

Garis lurus adalah kumpulan titik, yang masing-masing dapat diperoleh dari yang sebelumnya dengan mentransfer ke vektor yang sejajar satu sama lain. Misalnya, ada titik M dan N. Vektor MN¯ yang menghubungkannya memetakan M ke N. Ada juga titik ketiga P. Jika vektor MP¯ atau NP¯ sejajar dengan MN¯, maka ketiga titik tersebut terletak pada garis lurus yang sama dan membentuknya.

Bergantung pada dimensi ruang, persamaan yang mendefinisikan garis lurus dapat berubah bentuknya. Jadi, ketergantungan linier yang terkenal dari koordinat y pada x dalam ruang menggambarkan bidang yang sejajar dengan sumbu z ketiga. Dalam hal ini, dalam artikel ini kita hanya akan mempertimbangkan persamaan vektor untuk garis lurus. Ini memiliki penampilan yang sama untuk bidang dan ruang tiga dimensi.

Dalam ruang, garis lurus dapat ditentukan dengan ekspresi berikut:

(x; y; z) = (x 0; y 0; z 0) + * (a; b; c)

Di sini, nilai koordinat dengan indeks nol sesuai dengan titik yang termasuk dalam garis lurus, u¯ (a; b; c) adalah koordinat vektor arah yang terletak pada garis lurus ini, adalah bilangan real arbitrer , mengubah yang Anda bisa mendapatkan semua titik dari garis lurus. Persamaan ini disebut persamaan vektor.

Seringkali persamaan di atas ditulis dalam bentuk terbuka:

Dengan cara yang sama, Anda dapat menulis persamaan untuk garis lurus yang terletak di bidang, yaitu dalam ruang dua dimensi:

(x; y) = (x 0; y 0) + * (a; b);

persamaan bidang

Untuk dapat menemukan jarak dari suatu titik ke bidang proyeksi, Anda perlu mengetahui bagaimana bidang itu didefinisikan. Sama seperti garis lurus, itu dapat direpresentasikan dalam beberapa cara. Di sini kita akan mempertimbangkan satu saja: persamaan umum.

Misalkan titik M (x 0; y 0; z 0) termasuk dalam bidang, dan vektor n¯ (A; B; C) tegak lurus terhadapnya, maka untuk semua titik (x; y; z) dari pesawat persamaan akan menjadi benar:

A * x + B * y + C * z + D = 0, di mana D = -1 * (A * x 0 + B * y 0 + C * z 0)

Harus diingat bahwa dalam persamaan umum bidang ini, koefisien A, B dan C adalah koordinat vektor yang normal terhadap bidang.

Perhitungan jarak dengan koordinat

Sebelum melanjutkan ke pertimbangan proyeksi pada bidang suatu titik dan pada garis lurus, harus diingat bagaimana jarak antara dua titik yang diketahui harus dihitung.

Biarkan ada dua titik spasial:

A 1 (x 1; y 1; z 1) dan A 2 (x 2; y 2; z 2)

Kemudian jarak antara mereka dihitung dengan rumus:

A 1 A 2 = ((x 2 -x 1) 2 + (y 2 -y 1) 2 + (z 2 -z 1) 2)

Ekspresi ini juga digunakan untuk menentukan panjang vektor A 1 A 2 .

Untuk kasus pada bidang, ketika dua titik diberikan hanya dengan sepasang koordinat, persamaan yang serupa dapat ditulis tanpa kehadiran suku dengan z di dalamnya:

A 1 A 2 = ((x 2 -x 1) 2 + (y 2 -y 1) 2)

Sekarang kita akan mempertimbangkan berbagai kasus proyeksi pada bidang suatu titik pada garis lurus dan pada bidang dalam ruang.

Titik, garis dan jarak antara keduanya

Misalkan ada beberapa titik dan garis lurus:

P 2 (x 1; y 1);

(x; y) = (x 0; y 0) + * (a; b)

Jarak antara benda-benda geometris ini akan sesuai dengan panjang vektor, yang awalnya terletak di titik P 2, dan ujungnya berada di titik P pada garis lurus yang ditentukan, di mana vektor P 2 P dari garis lurus ini tegak lurus. Titik P disebut proyeksi titik P 2 ke garis yang ditinjau.

Di bawah ini adalah gambar yang menunjukkan titik P 2, jaraknya d ke garis lurus, dan vektor arah v 1 . Juga, titik sembarang P 1 dipilih pada garis lurus dan sebuah vektor ditarik darinya ke P 2. Titik P di sini bertepatan dengan tempat perpotongan garis tegak lurus.

Terlihat bahwa panah jingga dan merah membentuk jajar genjang, yang sisi-sisinya adalah vektor P 1 P 2 dan v 1 , dan tingginya adalah d. Diketahui dari geometri bahwa untuk menemukan tinggi jajar genjang, luasnya harus dibagi dengan panjang alas yang tegak lurusnya diturunkan. Karena luas jajaran genjang dihitung sebagai produk silang dari sisi-sisinya, kami mendapatkan rumus untuk menghitung d:

d = || / | v 1 |

Semua vektor dan koordinat titik dalam ekspresi ini diketahui, sehingga Anda dapat menggunakannya tanpa melakukan transformasi apa pun.

Masalah ini bisa diselesaikan secara berbeda. Untuk melakukannya, tuliskan dua persamaan:

• produk skalar dari P 2 P oleh v 1 harus sama dengan nol, karena vektor-vektor ini saling tegak lurus;
• koordinat titik P harus memenuhi persamaan garis lurus.

Persamaan ini cukup untuk mencari koordinat P, dan kemudian panjang d sesuai dengan rumus yang diberikan pada paragraf sebelumnya.

Masalah mencari jarak antara garis dan titik

Mari kita tunjukkan bagaimana menggunakan informasi teoretis ini untuk memecahkan masalah tertentu. Misalkan titik dan garis berikut diketahui:

(x; y) = (3; 1) - * (0; 2)

Penting untuk menemukan titik proyeksi ke garis lurus di pesawat, serta jarak dari M ke garis lurus.

Mari kita tunjukkan proyeksi yang ditemukan oleh titik M 1 (x 1; y 1). Kami akan memecahkan masalah ini dengan dua cara, yang dijelaskan dalam paragraf sebelumnya.

Metode 1. Vektor arah v 1 memiliki koordinat (0; 2). Untuk membangun jajaran genjang, pilih titik yang termasuk dalam garis lurus. Misalnya, titik dengan koordinat (3; 1). Maka vektor sisi kedua jajar genjang akan memiliki koordinat:

(5; -3) - (3; 1) = (2; -4)

Sekarang Anda perlu menghitung produk vektor yang mendefinisikan sisi jajar genjang:

Mengganti nilai ini ke dalam rumus, kita mendapatkan jarak d dari M ke garis lurus:

Metode 2. Sekarang mari kita cari dengan cara yang berbeda tidak hanya jarak, tetapi juga koordinat proyeksi M ke garis lurus, seperti yang dipersyaratkan oleh kondisi masalah. Seperti disebutkan di atas, untuk menyelesaikan masalah, perlu untuk membuat sistem persamaan. Ini akan mengambil bentuk:

(x 1 -5) * 0 + (y 1 +3) * 2 = 0;

(x 1; y 1) = (3; 1) -α * (0; 2)

Kami memecahkan sistem ini:

Proyeksi asal koordinat memiliki M 1 (3; -3). Maka jarak yang dibutuhkan sama dengan:

d = | MM 1 | = (4 + 0) = 2

Seperti yang Anda lihat, kedua metode penyelesaian memberikan hasil yang sama, yang menunjukkan kebenaran operasi matematika yang dilakukan.

Arahkan ke proyeksi bidang

Sekarang mari kita perhatikan proyeksi suatu titik di ruang angkasa ke bidang tertentu. Mudah ditebak bahwa proyeksi ini juga merupakan titik, yang, bersama dengan yang asli, membentuk vektor yang tegak lurus terhadap bidang.

Misalkan proyeksi ke bidang titik M memiliki koordinat berikut:

Pesawat itu sendiri dijelaskan oleh persamaan:

A * x + B * y + C * z + D = 0

Berdasarkan data tersebut, kita dapat merumuskan persamaan garis lurus yang memotong bidang tegak lurus dan melalui M dan M 1:

(x; y; z) = (x 0; y 0; z 0) + * (A; B; C)

Di sini, variabel dengan indeks nol adalah koordinat titik M. Posisi pada bidang titik M 1 dapat dihitung berdasarkan fakta bahwa koordinatnya harus memenuhi kedua persamaan tertulis. Jika persamaan ini tidak cukup untuk menyelesaikan masalah, maka kondisi paralelisme MM 1 dan vektor arah untuk bidang tertentu dapat digunakan.

Jelas, proyeksi titik milik pesawat bertepatan dengan dirinya sendiri, dan jarak yang sesuai adalah nol.

Soal titik dan bidang

Biarkan titik M (1; -1; 3) dan bidang diberikan, yang dijelaskan oleh persamaan umum berikut:

Hitung koordinat proyeksi ke bidang titik dan hitung jarak antara benda-benda geometris ini.

Untuk memulainya, kita buat persamaan garis lurus yang melalui M dan tegak lurus terhadap bidang yang ditunjukkan. Sepertinya:

(x; y; z) = (1; -1; 3) + * (- 1; 3; -2)

Mari kita tentukan titik di mana garis ini memotong bidang, M 1. Persamaan bidang dan garis lurus harus dipenuhi jika koordinat M 1 disubstitusikan ke dalamnya. Dengan menuliskan persamaan garis lurus secara eksplisit, kita memperoleh empat persamaan berikut:

X 1 + 3 * y 1 -2 * z 1 + 4 = 0;

y 1 = -1 + 3 * ;

Dari persamaan terakhir, kita peroleh parameter , lalu kita substitusikan ke kedua dari belakang dan ke dalam ekspresi kedua, kita dapatkan:

y 1 = -1 + 3 * (3-z 1) / 2 = -3 / 2 * z 1 + 3,5;

x 1 = 1 - (3-z 1) / 2 = 1/2 * z 1 - 1/2

Kami mengganti ekspresi untuk y 1 dan x 1 ke dalam persamaan untuk bidang, kami memiliki:

1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3.5) -2 * z 1 + 4 = 0

Dari mana kita mendapatkan:

y 1 = -3 / 2 * 15/7 + 3,5 = 2/7;

x 1 = 1/2 * 15/7 - 1/2 = 4/7

Kami telah menentukan bahwa proyeksi titik M ke bidang yang diberikan sesuai dengan koordinat (4/7; 2/7; 15/7).

Sekarang mari kita hitung jarak | MM 1 |. Koordinat vektor yang sesuai adalah:

MM 1 (-3/7; 9/7; -6/7)

Jarak yang dibutuhkan sama dengan:

d = | MM 1 | = 126 / 7 1.6

Tiga titik proyeksi

Selama pembuatan gambar, seringkali perlu untuk mendapatkan proyeksi bagian pada tiga bidang yang saling tegak lurus. Oleh karena itu, berguna untuk mempertimbangkan proyeksi beberapa titik M dengan koordinat (x 0; y 0; z 0) pada tiga bidang koordinat.

Tidak sulit untuk menunjukkan bahwa bidang xy dijelaskan oleh persamaan z = 0, bidang xz sesuai dengan ekspresi y = 0, dan bidang yz yang tersisa dilambangkan dengan persamaan x = 0. Mudah ditebak bahwa proyeksi suatu titik pada 3 bidang akan sama:

untuk x = 0: (0; y 0; z 0);

untuk y = 0: (x 0; 0; z 0);

untuk z = 0: (x 0; y 0; 0)

Di mana penting untuk mengetahui proyeksi suatu titik dan jaraknya ke bidang?

Menentukan posisi proyeksi titik pada bidang tertentu adalah penting ketika menemukan besaran seperti luas permukaan dan volume untuk prisma miring dan piramida. Misalnya, jarak dari puncak piramida ke bidang alasnya adalah tingginya. Yang terakhir termasuk dalam rumus untuk volume gambar ini.

Rumus dan metode yang dipertimbangkan untuk menentukan proyeksi dan jarak dari suatu titik ke garis dan bidang cukup sederhana. Penting untuk mengingat bentuk persamaan bidang dan garis yang sesuai, serta memiliki imajinasi spasial yang baik agar berhasil menerapkannya.