Temukan jarak dari suatu titik ke pesawat secara online. Jarak dari titik ke bidang: definisi dan contoh penemuan. Algoritma umum untuk mencari jarak dari titik $ M_0 $ ke pesawat

Kondisi Paralelisme dan Perpendicularity

1 °. Kondisi koplanaritas dua bidang

Biarkan dua pesawat diberikan:

A 1 x + B 1 kamu + C 1 z + D 1 = 0, n 1 = {A 1 ; B 1 ; C 1 } ≠ 0 ;(1)

A 2 x + B 2 kamu + C 2 z + D 2 = 0, n 2 = {A 2 ; B 2 ; C 2 } ≠ 0 .(2)

Kapan mereka coplanar (yaitu paralel atau sama)? Jelas, ini akan terjadi jika dan hanya jika vektor normalnya kolinear. Menerapkan kriteria coplanarity, kami memperoleh

Proposisi 1. Dua bidang dikatakan sebidang jika dan hanya jika produk vektor dari vektor normalnya sama dengan vektor nol:

[n 1 , n 2 ] = 0 .

2 °. Kondisi kebetulan dua pesawat

Proposisi 2. Bidang (1) dan (2) bertepatan jika dan hanya jika keempat koefisiennya proporsional, yaitu, terdapat bilangan sedemikian rupa sehingga

A 2 = A 1 , B 2 = B 1 , C 2 = C 1 , D 2 = D 1 . (3)

Bukti. Biarkan kondisi (3) terpenuhi. Maka persamaan bidang kedua dapat ditulis sebagai berikut:

λ A 1 x + λ B 1 kamu + λ C 1 z + λ D 1 = 0.

0, jika tidak maka akan menjadi A 2 = B 2 = C 2 = D 2 = 0, yang bertentangan dengan kondisi n 2 ≠ 0 ... Oleh karena itu, persamaan terakhir ekuivalen dengan persamaan (1), yang berarti kedua bidang berhimpitan.

Misalkan sekarang, sebaliknya, diketahui bahwa pesawat-pesawat ini bertepatan. Maka vektor normalnya adalah collinear, yaitu terdapat bilangan sedemikian sehingga

A 2 = A 1 , B 2 = B 1 , C 2 = C 1 .

Persamaan (2) sekarang dapat ditulis ulang sebagai:

λ A 1 x + λ B 1 kamu + λ C 1 z + D 2 = 0.

Mengalikan persamaan (1) dengan , kita memperoleh persamaan ekuivalen untuk bidang pertama (karena 0):

λ A 1 x + λ B 1 kamu + λ C 1 z + λ D 1 = 0.

Mari kita ambil beberapa poin ( x 0 , kamu 0 , z 0) dari bidang pertama (dan karena itu yang kedua) dan substitusikan koordinatnya ke dalam dua persamaan terakhir; kita mendapatkan persamaan yang benar:

λ A 1 x 0 + λ B 1 kamu 0 + λ C 1 z 0 + D 2 = 0 ;

λ A 1 x 0 + λ B 1 kamu 0 + λ C 1 z 0 + λ D 1 = 0.

Kurangi bagian bawah dari atas, kita dapatkan D 2 - D 1 = 0, yaitu D 2 = D 1, QED.

3 °. Syarat tegak lurus dua bidang

Jelas, untuk ini perlu dan cukup bahwa vektor-vektor normal harus tegak lurus.

Proposisi 3. Dua bidang tegak lurus jika dan hanya jika produk skalar vektor normal adalah nol:

(n 1 , n 2) = 0 .

Biarkan persamaan bidang diberikan

Kapak + Oleh + Cz + D = 0, n = {A; B; C} ≠ 0 ,

dan titik M 0 = (x 0 , kamu 0 , z 0). Kami memperoleh rumus untuk jarak dari titik ke bidang:

Ambil titik sewenang-wenang Q = (x 1 , kamu 1 , z 1) berbaring di pesawat ini. Koordinatnya memenuhi persamaan bidang:

Kapak 1 + Oleh 1 + Cz 1 + D = 0.

Perhatikan sekarang bahwa jarak yang dibutuhkan D sama dengan nilai absolut dari proyeksi vektor pada arah vektor n (di sini kita mengambil proyeksi sebagai nilai numerik, bukan sebagai vektor). Selanjutnya, kami menerapkan rumus untuk menghitung proyeksi:

Rumus serupa berlaku untuk jarak D dari titik M 0 = (x 0 , kamu 0) bidang ke garis lurus yang diberikan oleh persamaan umum Kapak + Oleh + C = 0.

SOAL C2 UJIAN UNIFIED NEGARA DALAM MATEMATIKA UNTUK MENEMUKAN JARAK DARI TITIK KE BIDANG

Kulikova Anastasia Yurievna

Mahasiswa tahun ke-5, jurusan matras. analisis, aljabar dan geometri EI KFU, RF, Republic of Tatarstan, Elabuga

Ganeeva Aigul Rifovna

penasihat ilmiah, Ph.D. ped. Sci., Associate Professor, EI KFU, RF, Republik Tatarstan, Elabuga

Dalam beberapa tahun terakhir, tugas untuk menghitung jarak dari suatu titik ke bidang telah muncul dalam tugas-tugas ujian matematika. Dalam artikel ini, dengan menggunakan contoh satu masalah, berbagai metode untuk menemukan jarak dari suatu titik ke bidang dipertimbangkan. Metode yang paling cocok dapat digunakan untuk menyelesaikan berbagai masalah. Setelah memecahkan masalah dengan satu metode, metode lain dapat memeriksa kebenaran hasil yang diperoleh.

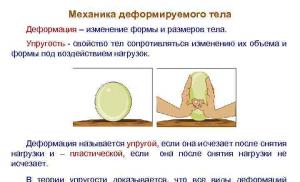
Definisi. Jarak dari suatu titik ke bidang yang tidak memuat titik ini adalah panjang segmen tegak lurus yang dijatuhkan dari titik ini ke bidang yang diberikan.

Tugas. Diberikan parallelepiped persegi panjang ABDENGANDA 1 B 1 C 1 D 1 dengan sisi AB=2, SM=4, A A 1 = 6. Tentukan jarak dari titik D ke pesawat SEBAGAID 1 .

1 cara. Menggunakan definisi... Tentukan jarak r ( D, SEBAGAID 1) dari titik D ke pesawat SEBAGAID 1 (gbr. 1).

Gambar 1. Metode pertama

Kami akan melaksanakan DH⊥SEBAGAI, oleh karena itu, dengan teorema tentang tiga tegak lurus D 1 H⊥SEBAGAI dan (DD 1 H)⊥SEBAGAI... Kami akan melaksanakan lurus DT tegak lurus D 1 H... Lurus DT terletak di pesawat DD 1 H, karenanya DT⊥AC... Karenanya, DT⊥SEBAGAID 1.

ADC cari hipotenusanya SEBAGAI dan tinggi DH

Dari segitiga siku-siku D 1 DH cari hipotenusanya D 1 H dan tinggi DT

Menjawab: .

Metode 2.metode volume (menggunakan piramida bantu). Masalah jenis ini dapat direduksi menjadi masalah menghitung tinggi piramida, dimana tinggi piramida adalah jarak yang diinginkan dari suatu titik ke bidang. Buktikan bahwa ketinggian ini adalah jarak yang diinginkan; temukan volume piramida ini dengan dua cara dan nyatakan tinggi ini.

Perhatikan bahwa dengan metode ini tidak perlu membangun tegak lurus dari titik tertentu ke bidang tertentu.

Rectangular parallelepiped - parallelepiped, yang semua wajahnya berbentuk persegi panjang.

AB=CD=2, SM=IKLAN=4, A A 1 =6.

Jarak yang diinginkan adalah ketinggian H piramida ACD 1 D dijatuhkan dari atas D atas dasar ACD 1 (gbr. 2).

Mari kita hitung volume piramida ACD 1 D dua arah.

Menghitung, cara pertama kita ambil sebagai basis ACD 1, maka

Menghitung, dengan cara kedua kita ambil sebagai basis ACD, kemudian

Menyamakan ruas kanan dari dua persamaan terakhir, kita peroleh

Gambar 2. Metode kedua

Dari segitiga siku-siku SEBAGAID, MENAMBAHKAN 1 , CDD 1 temukan sisi miring menggunakan teorema Pythagoras

ACD

Kami menghitung luas segitiga SEBAGAID 1 menggunakan rumus Heron

Menjawab: .

Metode 3. Metode koordinat.

Biarkan satu poin diberikan M(x 0 ,kamu 0 ,z 0) dan pesawat α diberikan oleh persamaan kapak+oleh+cz+D= 0 dalam sistem koordinat kartesius persegi panjang. Jarak dari titik M terhadap bidang dapat dihitung dengan rumus:

Mari kita perkenalkan sistem koordinat (Gbr. 3). Asal usul koordinat pada suatu titik V;

Lurus AB- sumbu NS, lurus matahari- sumbu kamu, lurus BB 1 - sumbu z.

Gambar 3. Metode ketiga

B(0,0,0), A(2,0,0), DENGAN(0,4,0), D(2,4,0), D 1 (2,4,6).

Biarlah Ax +oleh+ cz+ D= 0 - persamaan bidang ACD 1 . Mengganti koordinat titik ke dalamnya A, C, D 1 kita mendapatkan:

persamaan bidang ACD 1 akan mengambil formulir

Menjawab: .

Metode 4. Metode vektor.

Mari kita perkenalkan sebuah basis (Gbr. 4),.

Gambar 4. Metode keempat

Menemukan jarak dari suatu titik ke bidang adalah tugas yang sering muncul ketika memecahkan berbagai masalah geometri analitik, misalnya, tugas ini dapat direduksi menjadi menemukan jarak antara dua garis lurus yang bersilangan atau antara garis lurus dan bidang yang sejajar dengan dia.

Perhatikan bidang $ $ dan titik $ M_0 $ dengan koordinat $ (x_0; y_0; z_0) $, yang bukan termasuk bidang $ $.

Definisi 1

Jarak terpendek antara titik dan bidang adalah tegak lurus yang dijatuhkan dari titik $ _0 $ ke bidang $ $.

Gambar 1. Jarak dari titik ke bidang. Author24 - pertukaran online makalah siswa

Di bawah ini adalah cara mencari jarak dari suatu titik ke bidang dengan menggunakan metode koordinat.

Turunan rumus metode koordinat untuk mencari jarak dari titik ke bidang dalam ruang

Garis tegak lurus dari titik $ M_0 $, yang memotong bidang $ $ pada titik $ M_1 $ dengan koordinat $ (x_1; y_1; z_1) $, terletak pada garis lurus yang vektor arahnya adalah vektor normal pesawat $ $. Dalam hal ini, panjang vektor satuan $ n $ sama dengan satu. Dengan demikian, jarak dari $ $ ke titik $ M_0 $ adalah:

$ ρ = | \ vec (n) \ cdot \ vec (M_1M_0) | \ kiri (1 \ kanan) $, di mana $ \ vec (M_1M_0) $ adalah vektor normal bidang $ β $, dan $ \ vec ( n) $ adalah vektor normal satuan dari bidang yang ditinjau.

Dalam kasus ketika persamaan bidang diberikan dalam bentuk umum $ Ax + By + Cz + D = 0 $, koordinat vektor normal bidang adalah koefisien dari persamaan $ \ (A; B; C \) $, dan vektor normal satuan dalam hal ini memiliki koordinat yang dihitung dengan persamaan berikut:

$ \ vec (n) = \ frac (\ (A; B; C \)) (\ sqrt (A ^ 2 + B ^ 2 + C ^ 2)) \ kiri (2 \ kanan) $.

Sekarang Anda dapat menemukan koordinat vektor normal $ \ vec (M_1M_0) $:

$ \ vec (M_0M_1) = \ (x_0 - x_1; y_0-y_1; z_0-z_1 \) \ kiri (3 \ kanan) $.

Kami juga menyatakan koefisien $ D $ menggunakan koordinat titik yang terletak pada bidang $ $:

$ D = Kapak_1 + Samping_1 + Cz_1 $

Koordinat vektor normal satuan dari persamaan $ (2) $ dapat disubstitusikan ke dalam persamaan bidang $ $, maka diperoleh:

$ = \ frac (| A (x_0 -x_1) + B (y_0-y_1) + C (z_0-z_1) |) (\ sqrt (A ^ 2 + B ^ 2 + C ^ 2)) = \ frac ( | Ax_0 + By_0 + Cz_0- (Ax_1 + By_1 + Cz_1) |) (\ sqrt (A ^ 2 + B ^ 2 + C ^ 2)) = \ frac (Ax_0 + By_0 + Cz_0 + D) (\ sqrt (A ^ 2 + B ^ 2 + C ^ 2)) \ kiri (4 \ kanan) $

Persamaan $ (4) $ adalah rumus untuk mencari jarak dari suatu titik ke bidang dalam ruang.

Algoritma umum untuk mencari jarak dari titik $ M_0 $ ke pesawat

1. Jika persamaan bidang tidak diberikan dalam bentuk umum, pertama-tama Anda harus membawanya ke bentuk umum.
2. Setelah itu, perlu untuk menyatakan dari persamaan umum bidang vektor normal bidang yang diberikan melalui titik $ M_0 $ dan titik milik bidang yang diberikan; untuk ini, kita harus menggunakan persamaan $ (3) $ .
3. Tahap selanjutnya adalah pencarian koordinat vektor normal satuan bidang dengan menggunakan rumus $(2)$.
4. Terakhir, Anda dapat mulai mencari jarak dari suatu titik ke bidang, hal ini dilakukan dengan menghitung perkalian titik dari vektor $ \ vec (n) $ dan $ \ vec (M_1M_0) $.

, Kompetisi "Presentasi untuk pelajaran"

Kelas: 11

Presentasi pelajaran

Mundur ke depan

Perhatian! Pratinjau slide hanya untuk tujuan informasi dan mungkin tidak mewakili semua opsi presentasi. Jika Anda tertarik dengan karya ini, silakan unduh versi lengkapnya.

Sasaran:

• generalisasi dan sistematisasi pengetahuan dan keterampilan siswa;
• pengembangan keterampilan menganalisis, membandingkan, menarik kesimpulan.

Peralatan:

• proyektor multimedia;
• komputer;
• lembar kerja dengan teks tugas

PROSES PELAJARAN

I. Momen organisasi

II. Tahap pembaruan pengetahuan(slide 2)

Kami ulangi bagaimana jarak dari titik ke bidang ditentukan

AKU AKU AKU. Kuliah(slide 3-15)

Dalam pelajaran ini, kita akan melihat berbagai cara untuk mencari jarak dari suatu titik ke bidang.

Metode pertama: komputasi langkah demi langkah

Jarak dari titik M ke bidang :
- sama dengan jarak ke bidang dari titik sembarang P yang terletak pada garis lurus a, yang melewati titik M dan sejajar dengan bidang ;
- sama dengan jarak ke bidang dari titik sembarang P yang terletak pada bidang , yang melalui titik M dan sejajar dengan bidang .

Mari kita selesaikan tugas-tugas berikut:

№1. Pada kubus A ... D 1 tentukan jarak dari titik C 1 ke bidang AB 1 C.

Tetap menghitung nilai panjang segmen O 1 N.

№2. Dalam sebuah prisma heksagonal beraturan A ... F 1, semua sisinya sama dengan 1, tentukan jarak dari titik A ke bidang DEA 1.

Metode selanjutnya: metode volume.

Jika volume piramida ABCM sama dengan V, maka jarak dari titik M ke bidang yang mengandung ABS dihitung dengan rumus (M; ) = (M; ABC) =
Saat memecahkan masalah, kami menggunakan kesetaraan volume satu gambar, yang dinyatakan dalam dua cara berbeda.

Mari kita selesaikan masalah berikut:

№3. Tepi AD piramida DABC tegak lurus terhadap bidang alas ABC. Hitunglah jarak dari A ke bidang yang melalui titik tengah rusuk AB, AC dan AD, jika.

Saat memecahkan masalah metode koordinat jarak dari titik M ke bidang dapat dihitung dengan rumus (M; ) = , di mana M (x 0; y 0; z 0), dan bidang diberikan oleh persamaan ax + by + cz + d = 0

Mari kita selesaikan masalah berikut:

№4. Pada kubus satuan A ... D 1 tentukan jarak dari titik A1 ke bidang BDC 1.

Kami memperkenalkan sistem koordinat dengan asal di titik A, sumbu y akan berjalan di sepanjang tepi AB, sumbu x di sepanjang tepi AD, dan sumbu z di sepanjang tepi AA 1. Maka koordinat titik B (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Mari kita buat persamaan bidang yang melalui titik B, D, C 1.

Maka - dx - dy + dz + d = 0 x + y - z - 1 = 0. Oleh karena itu, =

Metode selanjutnya yang dapat digunakan ketika memecahkan masalah jenis ini adalah - metode tugas pendukung.

Penerapan metode ini terdiri dari penerapan masalah pendukung yang diketahui, yang dirumuskan sebagai teorema.

Mari kita selesaikan masalah berikut:

№5. Pada kubus satuan A ... D 1 tentukan jarak dari titik D 1 ke bidang AB 1 C.

Pertimbangkan aplikasinya metode vektor.

№6. Pada kubus satuan A ... D 1 tentukan jarak dari titik A 1 ke bidang BDC 1.

Jadi, kami melihat berbagai metode yang dapat digunakan untuk memecahkan masalah jenis ini. Pilihan metode ini atau itu tergantung pada tugas spesifik dan preferensi Anda.

IV. Bekerja dalam kelompok

Cobalah untuk memecahkan masalah dengan cara yang berbeda.

№1. rusuk kubus A...D1 sama besar. Tentukan jarak dari titik C ke bidang BDC 1.

№2. Hitunglah jarak dari titik A ke bidang BDC pada segi empat ABCD beraturan dengan sisi

№3. Pada prisma segitiga beraturan ABCA 1 B 1 C 1 yang semua rusuknya sama dengan 1, tentukan jarak dari A ke bidang BCA 1.

№4. Dalam sebuah piramida segi empat beraturan SABCD dengan semua sisi sama dengan 1, tentukan jarak dari A ke bidang SCD.

V. Ringkasan pelajaran, pekerjaan rumah, refleksi

Artikel ini berbicara tentang menentukan jarak dari suatu titik ke bidang. kita akan mengurai metode koordinat, yang memungkinkan kita menemukan jarak dari titik tertentu dalam ruang tiga dimensi. Untuk mengkonsolidasikan, pertimbangkan contoh beberapa tugas.

Jarak dari suatu titik ke bidang ditemukan melalui jarak yang diketahui dari suatu titik ke suatu titik, di mana salah satunya diberikan, dan yang lainnya adalah proyeksi ke bidang tertentu.

Ketika sebuah titik M 1 dengan bidang ditentukan dalam ruang, maka garis lurus yang tegak lurus terhadap bidang dapat ditarik melalui titik tersebut. H 1 adalah titik perpotongan mereka. Oleh karena itu, kami menemukan bahwa segmen M 1 H 1 adalah garis tegak lurus yang ditarik dari titik M 1 ke bidang , di mana titik H 1 adalah alas dari tegak lurus.

Definisi 1

Jarak dari titik tertentu ke dasar garis tegak lurus disebut, yang ditarik dari titik tertentu ke bidang tertentu.

Definisi dapat ditulis dalam formulasi yang berbeda.

Definisi 2

Jarak dari titik ke bidang disebut panjang tegak lurus, yang ditarik dari titik tertentu ke bidang tertentu.

Jarak dari titik M 1 ke bidang ditentukan sebagai berikut: jarak dari titik M 1 ke bidang akan menjadi yang terkecil dari titik tertentu ke titik mana pun pada bidang. Jika titik 2 terletak pada bidang dan tidak sama dengan titik 2, maka kita mendapatkan segitiga siku-siku dengan bentuk М 2 H 1 H 2 , yang berbentuk persegi panjang, di mana ada kaki M 2 H 1, M 2 H 2 - sisi miring. Oleh karena itu, ini menyiratkan bahwa M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 dianggap miring, yang ditarik dari titik M 1 ke bidang . Kami memiliki bahwa tegak lurus yang ditarik dari titik tertentu ke bidang kurang miring, yang ditarik dari suatu titik ke bidang tertentu. Perhatikan kasus ini pada gambar di bawah ini.

Jarak dari titik ke bidang - teori, contoh, solusi

Ada sejumlah masalah geometri yang penyelesaiannya harus memuat jarak dari suatu titik ke bidang. Cara mendeteksinya bisa berbeda. Untuk penyelesaiannya, gunakan teorema Pythagoras atau persamaan segitiga. Ketika, menurut kondisinya, perlu untuk menghitung jarak dari suatu titik ke bidang, yang diberikan dalam sistem koordinat persegi panjang ruang tiga dimensi, diputuskan dengan metode koordinat. Klausa ini membahas metode ini.

Dengan kondisi masalah, kita memiliki titik ruang tiga dimensi dengan koordinat M 1 (x 1, y 1, z 1) diberikan bidang , maka perlu untuk menentukan jarak dari M 1 ke pesawat . Ada beberapa cara untuk mengatasi masalah ini.

Cara pertama

Metode ini didasarkan pada pencarian jarak dari suatu titik ke bidang menggunakan koordinat titik H 1 yang merupakan alas tegak lurus dari titik M 1 ke bidang . Selanjutnya, Anda perlu menghitung jarak antara M 1 dan H 1.

Untuk menyelesaikan masalah dengan cara kedua, digunakan persamaan normal bidang tertentu.

Cara kedua

Dengan syarat, kita mendapatkan bahwa H 1 adalah alas dari garis tegak lurus, yang diturunkan dari titik M 1 ke bidang . Kemudian kita tentukan koordinat (x 2, y 2, z 2) dari titik H 1. Jarak yang diperlukan dari 1 ke bidang ditemukan dengan rumus M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2, di mana M 1 (x 1, y 1, z 1) dan H 1 (x 2, y 2, z 2). Untuk menyelesaikannya, Anda perlu mencari tahu koordinat titik H 1.

Kami memiliki bahwa H 1 adalah titik perpotongan bidang dengan garis lurus a, yang melewati titik M 1, yang tegak lurus terhadap bidang . Oleh karena itu, perlu untuk membuat persamaan garis lurus yang melalui titik tertentu yang tegak lurus terhadap bidang tertentu. Saat itulah kita akan dapat menentukan koordinat titik H 1. Penting untuk menghitung koordinat titik perpotongan garis dan bidang.

Algoritma untuk mencari jarak dari titik dengan koordinat M 1 (x 1, y 1, z 1) ke bidang :

Definisi 3

• Buatlah persamaan garis lurus a yang melalui titik M 1 dan pada saat yang sama
• tegak lurus terhadap bidang ;
• cari dan hitung koordinat (x 2, y 2, z 2) titik H 1 yang merupakan titik
• perpotongan garis lurus a dengan bidang ;
• hitung jarak dari 1 ke menggunakan rumus M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2.

Cara ketiga

Dalam sistem koordinat persegi panjang yang diberikan O x y z terdapat bidang , maka kita memperoleh persamaan normal bidang berbentuk cos x + cos y + cos z - p = 0. Sehingga diperoleh jarak M 1 H 1 dengan titik M 1 (x 1, y 1, z 1) ditarik ke bidang , dihitung dengan rumus M 1 H 1 = cos x + cos y + cos z - hal. Rumus ini valid, karena ditetapkan berdasarkan teorema.

Dalil

Jika diberikan titik M 1 (x 1, y 1, z 1) dalam ruang tiga dimensi, memiliki persamaan normal bidang berbentuk cos x + cos y + cos z - p = 0, maka perhitungan jarak dari titik ke bidang M 1 H 1 dihasilkan dari rumus M 1 H 1 = cos x + cos y + cos z - p, karena x = x 1, y = y 1, z = z 1.

Bukti

Bukti teorema direduksi menjadi mencari jarak dari titik ke garis. Oleh karena itu, kami menemukan bahwa jarak dari M 1 ke bidang adalah modulus selisih antara proyeksi numerik vektor radius M 1 dengan jarak dari titik asal ke bidang . Kemudian kita dapatkan ekspresi M 1 H 1 = n p n → O M → - p. Vektor normal bidang berbentuk n → = cos , cos , cos , dan panjangnya sama dengan satu, npn → OM → adalah proyeksi numerik dari vektor OM → = (x 1, y 1 , z 1) dalam arah yang ditentukan oleh vektor n →.

Mari kita terapkan rumus untuk menghitung vektor skalar. Kemudian kita peroleh ekspresi untuk mencari vektor bentuk n →, OM → = n → npn → OM → = 1 npn → OM → = npn → OM →, karena n → = cos α, cos , cos z dan OM → = (x 1, y 1, z 1). Notasi koordinat akan berbentuk n →, OM → = cos x 1 + cos β y 1 + cos z 1, maka M 1 H 1 = npn → OM → - p = cos x 1 + cos Y 1 + cos z 1 - hal. Teorema terbukti.

Oleh karena itu, diperoleh bahwa jarak dari titik M 1 (x 1, y 1, z 1) ke bidang dihitung dengan mensubstitusikan ke ruas kiri persamaan normal bidang cos x + cos y + cos z - p = 0 alih-alih koordinat x, y, z x 1, y 1 dan z 1, berkaitan dengan titik M 1, mengambil nilai absolut dari nilai yang diperoleh.

Mari kita perhatikan contoh mencari jarak dari titik dengan koordinat ke bidang tertentu.

Contoh 1

Hitung jarak dari titik dengan koordinat M 1 (5, - 3, 10) ke bidang 2 x - y + 5 z - 3 = 0.

Larutan

Mari kita selesaikan masalah dengan dua cara.

Metode pertama dimulai dengan menghitung vektor arah garis lurus a. Dengan hipotesis, kami memiliki bahwa persamaan yang diberikan 2 x - y + 5 z - 3 = 0 adalah persamaan bidang bentuk umum, dan n → = (2, - 1, 5) adalah vektor normal dari bidang yang diberikan . Ini digunakan sebagai vektor arah dari garis lurus a, yang tegak lurus terhadap bidang tertentu. Anda harus menulis persamaan kanonik garis lurus di ruang angkasa yang melalui M 1 (5, - 3, 10) dengan vektor arah dengan koordinat 2, - 1, 5.

Persamaan akan berbentuk x - 5 2 = y - (- 3) - 1 = z - 10 5 x - 5 2 = y + 3 - 1 = z - 10 5.

Titik persimpangan harus ditentukan. Untuk melakukan ini, sebaiknya gabungkan persamaan ke dalam sistem transisi dari kanonik ke persamaan dua garis lurus yang berpotongan. Kami akan mengambil titik ini sebagai H 1. Kami mengerti

x - 5 2 = y + 3 - 1 = z - 10 5 - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 y + 3) = - 1 (z - 10) x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 x + 2 y + 1 = 0 5 x - 2 z - 5 = 0

Maka Anda harus mengizinkan sistem

x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3

Mari kita beralih ke aturan untuk menyelesaikan sistem menurut Gaussian:

1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ z = 0 6 = 0, y = - 1 10 10 + 2 z = - 1, x = - 1 - 2 y = 1

Kami mendapatkan bahwa H 1 (1, - 1, 0).

Kami menghitung jarak dari titik tertentu ke bidang. Kita ambil titik M 1 (5, - 3, 10) dan H 1 (1, - 1, 0) dan diperoleh

M 1 H 1 = (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 = 2 30

Solusi kedua adalah pertama-tama bawa persamaan yang diberikan 2 x - y + 5 z - 3 = 0 ke bentuk normalnya. Tentukan faktor normalisasi dan dapatkan 1 2 2 + (- 1) 2 + 5 2 = 1 30. Dari sini kita turunkan persamaan bidang 2 30 x - 1 30 y + 5 30 z - 3 30 = 0. Perhitungan ruas kiri persamaan dilakukan dengan substitusi x = 5, y = - 3, z = 10, dan perlu diambil jarak dari M 1 (5, - 3, 10) ke 2 x - y + 5 z - 3 = 0 modulo. Kami mendapatkan ekspresi:

M 1 H 1 = 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 = 60 30 = 2 30

Jawaban: 2 30.

Ketika bidang ditentukan dengan salah satu metode untuk menentukan bidang, maka Anda harus terlebih dahulu mendapatkan persamaan bidang dan menghitung jarak yang diinginkan menggunakan metode apa pun.

Contoh 2

Titik dengan koordinat M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1) ditentukan dalam ruang tiga dimensi. Hitung jarak dari M 1 ke bidang A B C.

Larutan

Pertama, Anda perlu menulis persamaan bidang yang melalui tiga titik yang diberikan dengan koordinat M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1) .

x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ xy - 2 z - 1 2 4 0 4 - 2 - 2 = 0 - 8 x + 4 y - 20 z + 12 = 0 2 x - y + 5 z - 3 = 0

Oleh karena itu, masalahnya memiliki solusi yang mirip dengan yang sebelumnya. Artinya jarak dari titik M 1 ke bidang A B C bernilai 2 30.

Jawaban: 2 30.

Mencari jarak dari titik tertentu pada bidang atau ke bidang yang sejajar lebih mudah dengan menerapkan rumus M 1 H 1 = cos x 1 + cos y 1 + cos z 1 - p. Dari sini kita peroleh bahwa persamaan normal bidang diperoleh dalam beberapa aksi.

Contoh 3

Tentukan jarak dari suatu titik tertentu dengan koordinat M 1 (- 3, 2, - 7) ke bidang koordinat O x y z dan bidang yang diberikan oleh persamaan 2 y - 5 = 0.

Larutan

Bidang koordinat O y z sesuai dengan persamaan bentuk x = 0. Untuk bidang O y z, itu normal. Oleh karena itu, perlu untuk mensubstitusi nilai x = - 3 di sisi kiri ekspresi dan mengambil modulus nilai jarak dari titik dengan koordinat M 1 (- 3, 2, - 7) ke bidang. Kami mendapatkan nilai yang sama dengan - 3 = 3.

Setelah transformasi, persamaan normal bidang 2 y - 5 = 0 akan mendapatkan bentuk y - 5 2 = 0. Kemudian Anda dapat menemukan jarak yang diperlukan dari titik dengan koordinat M 1 (- 3, 2, - 7) ke bidang 2 y - 5 = 0. Mengganti dan menghitung, kita mendapatkan 2 - 5 2 = 5 2 - 2.

Menjawab: Jarak yang diinginkan dari M 1 (- 3, 2, - 7) ke O y z bernilai 3, dan ke 2 y - 5 = 0 bernilai 5 2 - 2.

Jika Anda melihat kesalahan dalam teks, silakan pilih dan tekan Ctrl + Enter