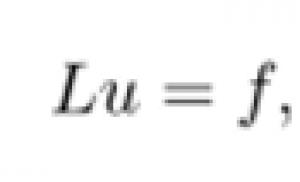Šeme razlike: eksplicitne i implicitne šeme. Metode za konstruisanje dijagrama Rješavanje mješovitog problema za talasnu jednačinu metodom mreže

Šema razlike

Šema razlike- ovo je konačan sistem algebarskih jednačina, stavljen u korespondenciju sa nekim diferencijalnim problemom koji sadrži diferencijalnu jednačinu i dodatne uslove (na primer, granične uslove i/ili početnu distribuciju). Dakle, diferencijalne šeme se koriste da se diferencijalni problem, koji ima kontinualnu prirodu, svede na konačan sistem jednačina, čije je numeričko rešenje u principu moguće na računarima. Algebarske jednadžbe stavljene u korespondenciju s diferencijalnom jednačinom dobijaju se metodom razlike, koja razlikuje teoriju razlika shema od drugih numeričkih metoda za rješavanje diferencijalnih problema (na primjer, projekcijske metode, kao što je Galerkinova metoda).

Rješenje diferencijalne sheme naziva se aproksimativno rješenje diferencijalnog problema.

Iako formalna definicija ne nameće značajna ograničenja na tip algebarskih jednadžbi, u praksi ima smisla razmatrati samo one sheme koje na neki način odgovaraju diferencijalnom problemu. Važni koncepti u teoriji diferencijskih shema su koncepti konvergencije, aproksimacije, stabilnosti i konzervativizma.

Aproksimacija

Kažu da se diferencijalni operator definiran na funkcijama definiranim u domeni aproksimira na određenoj klasi funkcija operatorom konačne razlike definiranim na funkcijama definiranim na mreži ovisno o koraku ako

Kaže se da je aproksimacija uredna ako

gdje je konstanta koja ovisi o specifičnoj funkciji, ali ne ovisi o koraku. Gore korištena norma može biti drugačija, a koncept aproksimacije ovisi o njegovom izboru. Često se koristi diskretni analog norme uniformnog kontinuiteta:

ponekad se koriste diskretni analozi integralnih normi.

Primjer. Aproksimacija operatora operatorom konačnih razlika

na ograničenom intervalu ima drugi red na klasi glatkih funkcija.

Problem konačne razlike aproksimira diferencijalni problem, a aproksimacija ima red , ako su i sama diferencijalna jednadžba i granični (i početni) uvjeti aproksimirani odgovarajućim operatorima konačnih razlika, a aproksimacije imaju red .

Courant uslov

Courant uslov (u literaturi na engleskom jeziku engleski. Courant-Friedrichs-Levy stanje , CFL) - brzina širenja poremećaja u problemu razlike ne bi trebala biti manja nego u diferencijalnom. Ako ovaj uvjet nije ispunjen, onda rezultat šeme razlike možda neće težiti rješavanju diferencijalne jednadžbe. Drugim riječima, u jednom vremenskom koraku čestica ne bi trebala „proći“ kroz više od jedne ćelije.

U slučaju shema čiji koeficijenti ne zavise od rješenja diferencijalne jednadžbe, Courantov uvjet slijedi iz stabilnosti.

Šeme na offset mrežama

U ovim šemama, mreže na kojima je dat rezultat i podaci su međusobno pomaknuti. Na primjer, točke rezultata su na sredini između tačaka podataka. U nekim slučajevima, ovo dozvoljava upotrebu jednostavnijih graničnih uslova.

vidi takođe

Linkovi

• “Šeme razlike” - Poglavlje u wiki knjigama na temu “Šeme razlike za hiperboličke jednačine”
• Demyanov A. Yu., Chizhikov D. V. Implicitna hibridna monotona razlika shema drugog reda tačnosti
• V. S. Ryabenkiy, A. F. Filippov. O stabilnosti razlika jednadžbi. - M.: Gostehizdat, 1956.
• S. K. Godunov, V. S. Ryabenky. Uvod u teoriju razlika shema. - M.: Fizmatgiz, 1962.
• K. I. Babenko. Osnove numeričke analize. - M.: Nauka, 1986.
• Berezin I.S., Zhidkov N.P. Metode obračuna, - Bilo koje izdanje.
• Bakhvalov N.S., Zhidkov N.P., Kobelkov G.M. Numeričke metode, - Bilo koje izdanje.
• G. I. Marchuk. Metode računske matematike. - M.: Nauka, 1977.

Bilješke

Wikimedia fondacija. 2010.

Pogledajte šta je "Šema razlike" u drugim rječnicima:

Sistem razlika jednadžbi koje aproksimiraju diferencijalnu jednačinu i dodatne (početne, granične, itd.) uslove. Aproksimacija originalnog diferencijalnog problema R. s. ovo je jedan od načina da se aproksimira diskretizacija originalnog problema... Mathematical Encyclopedia

razlika sheme konačnih elemenata- metoda konačnih elemenata - [A.S. Goldberg. Englesko-ruski energetski rječnik. 2006] Teme energija općenito Sinonimi metoda konačnih elemenata EN raspored razlike konačnih volumena ...

Diferencijalna šema je konačni sistem algebarskih jednačina, stavljen u korespondenciju sa bilo kojim diferencijalnim problemom koji sadrži diferencijalnu jednadžbu i dodatne uslove (na primjer, granični uvjeti i/ili početni ... ... Wikipedia

shema proračuna konačnih razlika zasnovana na kontrolnim zapreminama- (npr. prijenos topline i mase, toplotna provodljivost) [A.S. Goldberg. Englesko-ruski energetski rječnik. 2006] Energetske teme općenito EN kontrolna zapremina zasnovana na rasporedu konačnih razlika ... Vodič za tehnički prevodilac

Okvir: grafički dokument; prezentacija, slika, prezentacija nečega u najopštijim terminima, pojednostavljeno (na primjer, dijagram izvještaja); elektronički uređaj koji sadrži mnogo komponenti (integrirano kolo). Grafički dokument... ... Wikipedia

Diferencijalna shema konstruirana na osnovu varijacionog problema koji odgovara problemu granične vrijednosti za diferencijalnu jednačinu. Glavna ideja izgradnje R. v. With. je to sa posebnim izborom koordinatnih funkcija u Ritz metodi...... Mathematical Encyclopedia

Numeričke metode za rješavanje metoda za rješavanje jednadžbi giierbolpch. tip zasnovan na računskim algoritmima. Razne matematičke modeli u mnogim slučajevima dovode do hiperboličkih diferencijalnih jednadžbi. tip. Takve jednadžbe imaju tačan podatak ... ... Mathematical Encyclopedia

Grana računske matematike koja proučava metode za približno rješenje diferencijalnih jednačina zamjenjujući ih jednadžbama konačnih razlika (diferencijske šeme). R.s. t. proučava metode za konstruisanje razlika šema, ... ... Mathematical Encyclopedia

Numeričke metode za rješavanje parcijalnih diferencijalnih jednadžbi su metode aproksimativnog rješenja, zbog čega je rješenje problema predstavljeno tablicom brojeva. Tačna rješenja (u obliku eksplicitnih formula, serija i sl.) K.Z. mogu se ugraditi samo u rijetkim... Mathematical Encyclopedia

Metode rješavanja problema plinske dinamike zasnovane na računskim algoritmima. Razmotrimo glavne aspekte teorije numeričkih metoda za rješavanje problema plinske dinamike, pisanje jednadžbi plinske dinamike u obliku zakona održanja u inercijalnom... ... Mathematical Encyclopedia eBook

Primjer 1. Diferencijalna shema za Poissonovu jednačinu eliptičkog tipa.

Razmotrimo konstrukciju šeme razlike za prvi granični problem za jednačinu A u = f(x,y) u području koje je pravougaonik sa stranicama paralelnim s koordinatnim osa. Neka ovaj pravougaonik bude povezan sa uniformnom mrežom sa koracima h x I h y .

Problem graničnih vrijednosti

može se napisati u operatorskom obliku:

Imajte na umu da ovaj unos uključuje i granične uslove.

Zamjenom diferencijalnih operatora diferencijskim dobivamo jednadžbe

koji aproksimiraju originalnu diferencijalnu jednačinu sa drugim redom 0(h 2 + h 2) tačnost i rad na svim unutrašnjim tačkama regiona.

Različiti analozi graničnih uslova će imati oblik

Razlika aproksimacija diferencijalne jednačine zajedno sa analozima razlike graničnih uslova formiraju šemu razlike za Poissonovu jednačinu.

Po analogiji s problemom graničnih vrijednosti, shema razlike može se napisati u obliku operatora:

gdje su u L/ uključena i jednadžba razlike i granični uvjet razlike:

Jednadžba razlike povezuje vrijednosti mrežne funkcije u pet tačaka formiranja razlika obrazac za ovu jednačinu. U ovom slučaju, ovaj obrazac se zove krst. Može se zamisliti i drugi obrasci za ovu jednačinu.

Dobit ćemo približno rješenje problema diferencijalne granične vrijednosti ako odredimo vrijednosti mrežne funkcije na svim unutrašnjim čvorovima domene. Da biste to učinili, potrebno je zajednički riješiti sistem algebarskih linearnih jednadžbi čija je dimenzija jednaka broju unutrašnjih čvorova regije. U ovom slučaju govorimo o shemi implicitne razlike. Bilo koja vrijednost koja nas zanima Uij može se odrediti samo iz rješenja cjelokupnog problema razlike.

Što se tiče sistema jednačina, napominjemo dvije okolnosti.

• 1. Sistem ima veoma veliku dimenziju (M - 1) x (N- 1), a tradicionalne metode egzaktnog rješenja (na primjer, Gaussova metoda) zahtijevaju za rješenje broj algebarskih operacija proporcionalnih trećem stepenu dimenzije sistema.
• 2. Matrica sistema ima mnogo nultih elemenata (labava matrica). Ova okolnost omogućava razvoj ekonomičnih metoda za približna rješenja.

Razmatrana formulacija problema razlike tipična je za eliptičke jednačine. U plinskoj dinamici, ovo je oblik jednadžbe za funkciju strujanja ili za potencijal brzine. U drugim odeljcima ćemo pogledati efikasne metode za rešavanje takvih šema razlika.

Rice. 2.8.

PRI M 2. Diferencijalna šema za najjednostavniju paraboličku jednačinu (nestacionarna toplotna provodljivost u štapu jedinične dužine).

Razmotrite sljedeći problem:

Zapazimo da u slučaju paraboličke jednačine imamo otvoreno područje. Prilikom konstruiranja diferentne sheme javlja se nekoliko opcija za vezu između izvoda razlike u prostoru i vremenu.

Integrirajmo jednačinu u jednom vremenskom koraku:

U zavisnosti od toga koju kvadraturnu formulu koristimo za izračunavanje integrala na desnoj strani, dobićemo različite šeme razlike (slika 2.9).

Povezivanjem vremenske derivacije razlike sa prostornom derivacijom definisanom na P-ti vremenski sloj, dobijamo

eksplicitna 'šema razlike'

Ovo je ekvivalentno približnom izračunavanju integrala na desnoj strani (2.12), ali koristeći metodu lijevog pravokutnika.

Rice. 2.9. Mreža i šabloni za toplotnu jednačinu: A - površina i mreža; b- eksplicitni predložak sheme; V- šablon implicitne sheme; G- šablon familije kola sa šest tačaka; d- šablon dijagrama

"preskok"

Gornja formula također sadrži metodu za rješavanje jednadžbi mreže:

Vrijednost funkcije mreže u sljedećem vremenskom sloju

određuje se kroz poznate vrijednosti gf u prethodnom. Kretanje uzastopno u slojevima od početnog stanja njihov, 0) = y(x), rješenje se može naći u cijeloj računskoj domeni. Uzorak razlike za ovu šemu prikazan je na Sl. 2.9, b.

Procjena integrala kroz vrijednost integrala na sloju P+ 1, koristimo šablon razlike kao što je Sl. 2.9, b, a razlika analoga diferencijalne jednadžbe ima oblik

Da bi se pronašle vrijednosti mrežne funkcije u sljedećem vremenskom sloju, pri korištenju ove šeme razlike potrebno je zajednički riješiti onoliko jednačina oblika (2.14) koliko ima unutrašnjih čvorova koji se nalaze na P - 1-1. privremeni sloj. Uzimajući u obzir granične uslove = / n+1, Mg G +1 = m n+1, sistem nam omogućava da konstruišemo rešenje na sledećem vremenskom sloju sa poznatim vrednostima mrežne funkcije na prethodnom. Pomicanjem od početnih vrijednosti u slojevima, na svakom od kojih je potrebno riješiti sistem jednadžbi, moguće je konstruirati približno rješenje u cijeloj domeni.

Razmotrena shema razlike je primjer shema implicitne razlike, naziva se shema gledanja unaprijed ili čisto implicitna shema.

Obrazac razlike u šest tačaka generiše porodicu šema razlika, od kojih su prethodna dva posebni slučajevi:

At a = 0 imamo eksplicitnu šemu, sa a = I- implicitno sa unapred, sa A> 0 - implicitno. At A - 0,5 dobijamo simetričnu, široko poznatu u računarskoj praksi Crank Nicholsonov dijagram.

Gore navedene šeme, naravno, ne iscrpljuju čitavu raznolikost shema razlika zasnovanih na aproksimaciji razlika diferencijalnih operatora. Evo primjera eksplicitne sheme razlike zasnovane na centriranju vremenskih derivata, sheme koja koristi funkciju mreže na tri vremenska sloja:

Obrazac razlike obuhvata tri vremenska sloja. Shema ima drugi red aproksimacije iu vremenu iu prostornoj varijabli i eksplicitna je. Ova shema ima niz značajnih nedostataka, od kojih se većina može eliminirati zamjenom I” u aproksimaciji prostornog derivata prosječnom vrijednošću za dva vremenska sloja:

Tako dobijena eksplicitna troslojna shema

pozvao Dufortpe-Frankel šema, a odsustvo vrijednosti mrežne funkcije u centralnom čvoru objašnjava naziv "leapfrog", koji se ponekad koristi za šeme ove vrste.

Na primjerima je pokazano da je za isti granični problem moguće napisati nekoliko različitih dijagrama, tj. Istraživač ima na raspolaganju prilično veliki izbor. Koje uvjete mora zadovoljiti shema razlike da bi rješenje razlike odgovaralo rješenju originalnog diferencijalnog problema? Ovo pitanje će biti razmotreno u narednom odeljku.

konfiguraciju čvorova, vrijednosti mrežne funkcije u kojoj određuju oblik jednadžbi razlika u unutrašnjim (negraničnim) tačkama mreže. U pravilu, na slikama sa slikama predložaka, tačke uključene u izračunavanje derivata su povezane linijama.

Courant-Isakson-Ries shema(KIR), koji se ponekad povezuje i sa imenom S.K. Godunov, ispada kada, . Njegov red aproksimacije je . KIR šema je uslovno stabilna, tj. kada je ispunjen Courantov uslov . Predstavimo jednadžbe razlike za Courant-Isakson-Ries shemu u unutrašnjim točkama računske domene:

Ove sheme, koje se nazivaju i shema s razlikama uz vjetar (u engleskoj literaturi - upwind) mogu se napisati u obliku

Njihova prednost je precizniji obračun područja zavisnosti rješenja. Ako uvedemo notaciju

tada se obje šeme mogu napisati u sljedećim oblicima:

(forma toka razlike jednadžbe);

(ovdje je jasno istaknut pojam sa drugom razlikom, što shemi daje stabilnost);

(jednačina u konačnim koracima).

Hajde da razmotrimo metoda nesigurnih koeficijenata da se konstruiše dijagram, desni ugao prvog reda tačnosti za jednačinu transporta

Šema se može predstaviti u obliku

Courant-Isakson-Reesova shema je usko povezana s numeričkim metodama karakteristika. Hajde da ukratko opišemo ideju takvih metoda.

Posljednje dvije dobijene sheme (sa različitim predznacima brzine prijenosa) mogu se protumačiti na sljedeći način. Konstruirajmo karakteristiku koja prolazi kroz čvor (t n + 1, x m), vrijednost na kojoj se mora odrediti, i siječe sloj t n u tački . Radi određenosti, pretpostavljamo da je brzina prijenosa c pozitivna.

Provodeći linearnu interpolaciju između čvorova x m - 1 i x m na donjem sloju u vremenu, dobijamo

Zatim prenosimo vrijednost u n (x") duž karakteristike bez promjene na gornji sloj t n + 1, tj. stavljamo . Prirodno je posljednju vrijednost uzeti u obzir kao približno rješenje homogena jednačina transfer. U ovom slučaju

ili, prelazak sa Courant broja ponovo na parametre mreže,

one. koristeći drugu metodu došli smo do već poznate sheme “lijevog ugla”, stabilne za . Kada se tačka preseka karakteristike koja napušta čvor (t n + 1, x m, sa n-tim slojem u vremenu) nalazi levo od čvora (t n, x m - 1). Dakle, da bi se pronašlo rešenje, potrebno je nije više interpolacija, već ekstrapolacija, što se ispostavilo da je nestabilno.

Nestabilnost šeme "desnog ugla" za c > 0 je takođe očigledna. Da bi se ovo dokazalo, može se koristiti ili spektralna karakteristika ili Courant, Friedrichs i Levy uslov. Slično razmišljanje se može izvesti i za slučaj c< 0 и схемы "правый уголок".

Nestabilno krug sa četiri tačke ispada kada , njegov red aproksimacije. Mrežne jednadžbe za šemu razlike imat će sljedeći oblik:

Lax-Wendroffova shema nastaje kada . Redoslijed aproksimacije Lax-Wendroffove sheme je . Shema je stabilna pod Courantovim uvjetom .

Ova šema se može dobiti ili metodom neodređenih koeficijenata, ili preciznijim uzimanjem u obzir vodećeg člana greške aproksimacije. Razmotrimo detaljnije proces izvođenja Lax-Wendroffove sheme. Provodeći studiju prethodne šeme u četiri tačke za aproksimaciju (a studija je prilično elementarna i svodi se na proširenje funkcije projekcije na mrežu tačnog rješenja diferencijalnog problema u Taylorovom nizu), dobijamo za glavni termin greške

Prilikom izvođenja izraza za glavni član greške aproksimacije korištena je posljedica originalne diferencijalne transportne jednadžbe

Što se dobija diferenciranjem originalne jednadžbe (3.3) prvo s obzirom na vrijeme t, zatim s obzirom na x koordinatu i oduzimanjem jedne od rezultirajućih relacija od druge.

Sljedeće, zamjena drugi derivat u drugom članu na desnoj strani sa tačnošću od O(h 2), dobijamo novu različitu šemu koja aproksimira originalnu diferencijalna jednadžba sa preciznošću . Mrežne jednadžbe za Lax-Wendroffovu shemu na unutrašnjim čvorovima računske mreže su

Implicitna šema u šest tačaka javlja se pri q = 0; kada je njegov red aproksimacije , u .

Koristeći šablon za svaki unutrašnji čvor regije rješenja, jednačina topline je aproksimirana

Odavde nalazimo:

Koristeći početne i granične uvjete, vrijednosti mrežne funkcije se nalaze u svim čvorovima na nultom vremenskom nivou.

Zatim koristeći relacije

vrijednosti ovih funkcija nalaze se u svim unutrašnjim čvorovima na prvom vremenskom nivou, nakon čega nalazimo vrijednost na graničnim čvorovima

Kao rezultat, nalazimo vrijednost karakteristika u svim čvorovima na prvom vremenskom nivou. Nakon toga, koristeći ove relacije nalazimo sve ostale vrijednosti itd.

U šemi razlike koja se razmatra, vrijednost željene funkcije na sljedećem vremenskom nivou nalazi se direktno, eksplicitno koristeći formulu

Stoga se dijagram razlike koji se razmatra pomoću ovog uzorka naziva eksplicitna razlika shema . Njegova tačnost je reda veličine.

Ova razlika shema je jednostavna za korištenje, ali ima značajan nedostatak. Ispostavilo se da je eksplicitna shema razlike ima stabilno rešenje samo u slučaju da, ako je uslov ispunjen :

Eksplicitna razlika shema je uslovno stabilan . Ako uvjet nije ispunjen, tada male greške u proračunu, na primjer, povezane sa zaokruživanjem računalnih podataka, dovode do nagle promjene rješenja. Rješenje postaje neupotrebljivo. Ovaj uslov nameće vrlo stroga ograničenja na vremenski korak, što može biti neprihvatljivo zbog značajnog povećanja vremena računanja za rješavanje ovog problema.

Razmislite o različitoj shemi koristeći drugačiji obrazac

Metoda 36

Implicitna razlika shema za jednadžbu topline.

Zamijenimo u jednačinu provođenja toplote:

Ova relacija je napisana za svaki interni čvor na vremenskoj razini i dopunjena je s dvije relacije koje određuju vrijednosti ​​na graničnim čvorovima. Rezultat je sistem jednadžbi za određivanje nepoznatih vrijednosti funkcije na vremenskom nivou.

Shema za rješavanje problema je sljedeća:

Koristeći početne i granične uslove, vrijednost funkcije se nalazi na nultom vremenskom nivou. Zatim, koristeći ove relacije i granične uslove, konstruiše se sistem linearnih algebarskih jednadžbi za pronalaženje vrednosti funkcije na prvom vremenskom nivou, nakon čega se sistem ponovo gradi koristeći ove relacije, a vrednosti se pronalaze na drugom vremenskom nivou itd.

Razlika od eksplicitne sheme- vrijednosti na sljedećem vremenskom nivou se ne izračunavaju direktno pomoću gotove formule, već se nalaze rješavanjem sistema jednačina, tj. vrijednosti nepoznatih se pronalaze implicitno rješavanjem SLAE. Stoga se shema razlike naziva implicitna. Za razliku od eksplicitnog, implicitno je apsolutno stabilno.

Tema br. 9

Problemi optimizacije.

Ovi problemi su među najvažnijim problemima u primijenjenoj matematici. Optimizacija znači odabirom najbolje opcije od svih mogućih rješenja zadatog problema. Da bi se to postiglo, potrebno je problem koji se rješava formulirati kao matematički, dajući kvantitativno značenje pojmovima bolje ili lošije. Obično je tokom procesa rješenja potrebno pronaći optimizirane vrijednosti parametara. Ovi parametri se nazivaju dizajn. I broj dizajnerskih parametara određuje dimenziju problema.

Kvantitativna procjena rješenja vrši se pomoću određene funkcije ovisno o projektnim parametrima. Ova funkcija se zove cilj . Konstruiran je tako da najoptimalnija vrijednost odgovara maksimumu (minimumu).

- ciljna funkcija.

Najjednostavniji slučajevi su kada funkcija cilja ovisi o jednom parametru i specificira se eksplicitnom formulom. Može postojati nekoliko ciljnih funkcija.

Na primjer, prilikom projektovanja aviona potrebno je istovremeno osigurati maksimalnu pouzdanost, minimalnu težinu i cijenu itd. U takvim slučajevima unesite sistem prioriteta . Svakoj funkciji cilja dodijeljen je određeni ciljni množitelj, što rezultira generaliziranom funkcijom cilja (kompromisna funkcija).

Optimalno rješenje je obično ograničeno brojnim uvjetima vezanim za fizičku funkciju problema. Ovi uslovi mogu biti u obliku jednakosti ili nejednakosti

Teorija i metode za rješavanje problema optimizacije u prisustvu ograničenja su predmet istraživanja u jednoj od grana primijenjene matematike - matematičko programiranje.

Ako je funkcija cilja linearna u odnosu na projektne parametre i ograničenja nametnuta parametrima su također linearna, tada problem linearnog programiranja . Razmotrimo metode za rješavanje jednodimenzionalnog problema optimizacije.

Potrebno je pronaći vrijednosti pri kojima funkcija cilja ima maksimalnu vrijednost. Ako se ciljna funkcija zada analitički i može se naći izraz za njene derivacije, tada će se optimalno rješenje postići ili na krajevima segmenta ili u tačkama u kojima derivacija nestaje. Ovo su kritične tačke i . Potrebno je pronaći vrijednosti ciljne funkcije u svim kritičnim točkama i odabrati maksimalnu.

Općenito, za pronalaženje rješenja koriste se različite metode pretraživanja. Kao rezultat, segment koji sadrži optimalno rješenje se sužava.

Pogledajmo neke od metoda pretraživanja. Pretpostavimo da ciljna funkcija na intervalu ima jedan maksimum. U ovom slučaju, dijeljenjem s čvornim točkama, čiji je broj , ciljna funkcija se izračunava na tim čvornim točkama. Pretpostavimo da će maksimalna vrijednost ciljne funkcije biti u čvoru , tada možemo pretpostaviti da se optimalno rješenje nalazi na intervalu . Kao rezultat toga, segment koji sadrži optimalno rješenje je sužen. Dobijeni novi segment se opet dijeli na dijelove itd. Sa svakom particijom, segment koji sadrži optimalno rješenje se smanjuje za faktor.

Pretpostavimo da su izvedeni koraci sužavanja. Tada se originalni segment smanjuje za faktor.

Odnosno, radimo to dok radi (*)

U ovom slučaju se izračunava funkcija cilja.

Potrebno je pronaći vrijednost tako da se izraz (*) dobije na najmanju

broj kalkulacija.

Metoda 37

Metoda polovičnog dijeljenja.

Razmotrimo metodu pretraživanja za . Zove se metoda prepolovljenja, jer se u svakom koraku segment koji sadrži optimalno rješenje prepolovi.

Efikasnost pretrage se može povećati posebnim odabirom tačaka u kojima se izračunava funkcija cilja u određenom koraku suženja.

Metoda 38

Metoda zlatnog preseka.

Jedan efikasan način je metoda zlatnog omjera. Zlatni presek segmenta je tačka za koju je uslov zadovoljen

Postoje dvije takve tačke: =0,382 +0,618

0,618 +0,382 .

Segment je podijeljen točkama i tada se nalazi tačka u kojoj je ciljna funkcija maksimalna. Kao rezultat, pronađen je modificirani segment dužine 0,618( - ).

Jedna vrijednost zlatnog presjeka za suženi segment je već poznata, pa je u svakom sljedećem koraku potrebno izračunati funkciju cilja samo u jednoj tački (druga tačka zlatnog preseka).

Metod 39

Metoda uspona po koordinatama (spuštanje).

Prijeđimo na razmatranje problema optimizacije u slučaju kada funkcija cilja ovisi o nekoliko vrijednosti parametara. Najjednostavniji način pretraživanja je metoda uspona (spuštanja) po koordinatama.

Postoje tri metode za izradu dijagrama razlika na datom predlošku:

· metoda aproksimacije razlike;

· metoda integro-interpolacije;

· metoda neodređenih koeficijenata.

Metoda aproksimacija razlike(24), (26) smo već koristili pri sastavljanju šema. Prema ovoj metodi, svaka derivacija uključena u jednadžbu i granični uvjet zamjenjuje se nekim izrazom razlike uzimajući u obzir čvorove datog šablona. Metoda olakšava konstruisanje dijagrama sa aproksimacijom prvog i drugog reda, kada su koeficijenti jednačine dovoljno glatke funkcije. Teško je generalizirati ovaj pristup na brojne važne slučajeve. Na primjer, ako su koeficijenti jednadžbe diskontinuirani, ili se pretpostavlja da se koristi nepravokutna i neujednačena mreža, dolazi do nesigurnosti u konstrukciji dijagrama.

Koristeći integro-interpolacijski metod ili balansna metoda koristiti dodatna fizička razmatranja, koja se svode na sastavljanje jednadžbi očuvanja za određene veličine. U ovoj metodi, nakon odabira predloška, ​​područje se dijeli na ćelije. Diferencijalna jednadžba se integrira preko ćelije i, koristeći formule vektorske analize, svodi na integralni oblik koji odgovara određenom integralnom zakonu. Integrali se izračunavaju približno pomoću jedne od kvadraturnih formula i dobija se dijagram razlike.

Predstavimo jednačinu toplotne provodljivosti sa promenljivim koeficijentom toplotne provodljivosti u obliku: . Za njegovu aproksimaciju biramo šablon prikazan na slici 8, gdje je odgovarajuća ćelija označena isprekidanom linijom.

Izvršimo integraciju preko ćelije:

i aproksimiramo prvi integral formulom prosjeka, a drugi integral formulom pravokutnika, tada

U posljednjem izrazu derivacije zamjenjujemo konačnim razlikama i, smatrajući da je mreža uniformna, dobijamo shemu razlike

Ako k= const, onda se shema (35) poklapa sa implicitnom shemom (24).

Fig.8. Šablon i ćelija integro-interpolacije
metoda za toplotnu jednačinu

Metoda integro-interpolacije je najkorisnija kada su koeficijenti jednačine neglatki ili čak diskontinuirani. U ovom slučaju, okretanje opštijim - integralnim zakonima - vraća nas na ispravnija generalizovana rešenja.

Razmotrimo primjer korištenja diferentne šeme (35) za izračunavanje toplinske provodljivosti medija koji se sastoji od tri medija sa različitim koeficijentima toplinske provodljivosti, tj.

(36)

Gdje k 1 , k 2 , k 3 su, općenito govoreći, različiti nenegativni brojevi. U ovom slučaju, originalna jednačina se može napisati kao:

(37)

Za izračunavanje pomoću šeme (35) sa koeficijentom toplotne provodljivosti (36), pretpostavićemo da

i na lijevoj strani x= 0 i desno x = a granice prema (37), održavat ćemo nultu temperaturu, tj. i .

Listing_br.4 prikazuje kod programa koji rješava jednačinu (36), (37) prema šemi razlike (35), (38).

Listing_No.4

%Program za rješavanje toplotne jednačine

%(37) sa koeficijentom razmaka

% toplinske provodljivosti (36)

globalno a k1 k2 k3

%definisati segment integracije i

%tri vrijednosti koeficijenta toplinske provodljivosti

% u tri područja intervala integracije

a=3; k1=0,1; k2=100; k3=10;

%odrediti korak u vremenu i prostoru

tau=0,05; h=0,05;

x=0:h:a; N=dužina(x);

% Izrada početne raspodjele temperature

ako je x(i)<=0.5*a

y(i)=((2*Tm)/a)*x(i);

ako je x(i)>0,5*a

y(i)=((2*Tm)/a)*(a-x(i));

%nacrtajte početni temperaturni profil

%debela crvena linija

plot(x,y,"Boja","crvena","Širina linije",3);

%izračunajte koeficijente sweep A(n), B(n)

%C(n): A(n)y2(n+1)+B(n)y2(n)+C(n)y2(n-1)=y(n)

A(n)=-(tau/h^2)*k(x(n)+0,5*h);

B(n)=1+(tau/h^2)*...

(k(x(n)+0,5*h)+k(x(n)-0,5*h));

C(n)=-(tau/h^2)*k(x(n)-0,5*h);

%definirajte lijevi granični uvjet

alfa(2)=0; beta(2)=0;

alfa(n+1)=-A(n)/(B(n)+C(n)*alfa(n));

beta(n+1)=(y(n)-C(n)*beta(n))/...

(B(n)+C(n)*alfa(n));

%postavite pravi granični uslov

za n=(N-1):-1:1

y(n)=alfa(n+1)*y(n+1)+beta(n+1);

%nacrtati trenutni temperaturni profil

% određuju koeficijent toplotne provodljivosti

globalno a k1 k2 k3

ako je (x>=0)&(x<=a/3)

ako je (x>a/3)&(x<=(2*a)/3)

ako je (x>(2*a)/3)&(x<=a)

Slika 9 prikazuje rezultat programskog koda u Listing_br.4. Početni trokutasti temperaturni profil je nacrtan podebljanom crvenom linijom. Vertikalne strelice na grafikonu razdvajaju područja sa različitim koeficijentima toplotne provodljivosti. Prema listing_no.4 kodu, koeficijenti toplotne provodljivosti se razlikuju jedan od drugog za tri reda veličine.

Fig.9. Rješenje jednačine topline (37) sa diskontinualnim
koeficijent toplotne provodljivosti (36)

Metoda neizvjesnih koeficijenata je da se linearna kombinacija rješenja na čvorovima određenog šablona uzima kao razlika sheme. Koeficijenti linearne kombinacije određuju se iz uslova maksimalnog reda odgovarajućeg ostatka u smislu t I h.

Dakle, za jednačinu u šablonu na slici 8 možemo napisati sljedeću šemu sa neodređenim koeficijentima

Određivanje ostatka

Zamijenimo onda (31) u (40).

(41)

Većina članova u (41) nestaje pod uslovom

. (42)

Zamjenom (42) u (39) dobijamo shemu razlike (24).

Metoda neodređenih koeficijenata primjenjiva je i na složenije slučajeve. Na primjer, za trokutastu mrežu, čiji je predložak prikazan na slici 10, možete dobiti sljedeću shemu razlike

Slika 10. Predložak trokutaste mreže za jednadžbu razlike (43)

Razmotrimo nepravilne čvorove sheme razlike, tj. njegove granične uslove. Za jednačinu toplote u t = k u xx granični čvorovi su nepravilni n= 0 i n = N. Ako se uzme u obzir prvi granični problem

tada je lako zapisati odgovarajuće uslove razlike

koji se izvode precizno, jer rezidual za njih je nula.

Složeniji je slučaj drugog graničnog problema, kada granični uslov sadrži izvod u odnosu na x. Na primjer, kada se specificira protok topline na rubovima, granični uvjeti imaju sljedeći oblik:

Izvodi u (44) mogu se aproksimirati desnom (lijevom) konačnom razlikom:

Nepodudarnost jednadžbi razlika (45) se lako procjenjuje:

(46)

Dakle, prema (46), diskrepancija graničnih uslova ima prvi red tačnosti u h, dok je u regularnim tačkama red tačnosti na drugom mestu h, tj. pri odabiru aproksimacije graničnih uslova pomoću formule (45) dolazi do gubitka tačnosti.

Da biste poboljšali tačnost graničnih uslova, razmotrite metoda fiktivne tačke. Uvedemo dvije fiktivne tačke izvan segmenta: , i napiši to tačkama n= 0 i n = N eksplicitna razlika shema (26), onda

Lijevi i desni granični uvjeti aproksimiramo koristeći središnju razliku, tj.

Isključujući fiktivne tačke i vrijednosti funkcija u njima iz (47), (48), nalazimo granične uslove drugog reda tačnosti u h:

(49)

Granični uslovi (49) su eksplicitni, jer sadrže samo jednu vrijednost na sljedećem sloju.

Osim metode fiktivne točke, postoji još jedna metoda za smanjenje neslaganja, univerzalnija je, ali manje vizualna. Hajde da se razgradimo u(t,x 1) u blizini x 0 onda

Prema (44), , a iz jednačine provođenja topline nalazimo . Zamjenjujući ove procjene u Taylorovu ekspanziju, nalazimo

Zamjenom u (50) dobijamo lijevi granični uvjet (49).

Prema gore navedenoj proceduri, može se postići povećana tačnost u aproksimaciji graničnih uslova.

Aproksimacija

Neka oblast bude data G varijable x = (x 1 ,x 2 ,…,xp) sa granicom G i postavlja se ispravan problem rješavanja jednadžbe sa rubnim uslovima:

Au(x) - f(x) = 0, x Î G; (51)

Ru(x) - m(x) = 0, x O G. (52)

Uđimo u područje G+ G mreža sa stepenicama h, koji sadrži regularne (interne) čvorove w h i nepravilni (granični) čvorovi g h.

Prijeđimo u (51), (52) na odgovarajuće analogne razlike

A h y h(x) - jh(x) = 0, x Î w h; (51¢)

R h y h(x) - c h(x) = 0, x Î g h. (52¢)

Blizina šeme razlike (51¢), (52¢) originalnom problemu (51), (52) određena je vrijednostima reziduala:

Diferencijalni krug (51¢), (52¢) približno problem (51), (52), kada

aproksimacija ima str th red kada

Dajemo neke komentare o izboru normi. Radi jednostavnosti, razmotrićemo jednodimenzionalni slučaj, tj. G = [a,b].

Možete koristiti Chebyshev ili lokalnu normu

,

ili Hilbertov srednji kvadrat:

.

Često se konstruiraju povezani ili povezani s operatorom A energetski standardi. Na primjer,

Izborom norme upravljaju dva suprotna razmatranja. S jedne strane, poželjno je da se razlika rješenja y bio blizu tačnog rješenja u najjačoj© normi. Na primjer, u problemima koji uključuju destrukciju konstrukcija, sitnost deformacija ne garantuje integritet konstrukcija, ali malenost normalnih jamči. S druge strane, što je norma slabija, lakše je konstruirati šemu razlike i dokazati njenu konvergenciju.

Funkcije y h, jh, c h, uključeni u (51¢), (52¢), definisani su na mreži, pa je za njih potrebno odrediti odgovarajuće mrežne norme , i . Obično se uvode tako da uđu u odabrane norme, i kada h® 0. Sljedeći izrazi su odabrani kao analogi razlike Čebiševljevih i Hilbertovih normi:

ili bliski analozi.

Održivost

Pod stabilnošću (nestabilnošću) diferentne šeme podrazumevamo da se male greške koje nastaju tokom procesa proračuna (ili koje se unose sa ulaznim podacima) smanjuju (povećavaju) u narednim proračunima.

Razmotrimo primjer nestabilne razlike sheme za Cauchyjev problem diferencijalne jednadžbe u¢ = a u. Odaberimo sljedeću jednoparametarsku familiju razlika shema:

. (53)

Ispitivanje rasta greške dy n početni podaci jednačine (53). Kako je jednadžba (53) linearna, greška dy n zadovoljava istu jednačinu (53). Hajde da proučimo posebnu vrstu greške dy n = l n. Zamijenimo onda ovu reprezentaciju u (53).

Rješenje kvadratne jednadžbe (54) at h® 0 daje sljedeće procjene za korijene

Iz procjena korijena u (55) slijedi da za s < ½ второй корень |l 2 | > 1, tj. u jednom koraku greška se povećava nekoliko puta. Hajde da to proverimo.

Listing_br.5 prikazuje kod programa koji ilustruje proračun za nestabilne uslove s= 0,25 šema (53) i prema stabilnoj šemi na s= 0,75. U početnim podacima odabrani su mali poremećaji. Zatim je izvršena serija proračuna sa opadajućom vrijednošću koraka mreže h. Na slici 11 prikazani su konačni grafovi zavisnosti vrijednosti perturbacije u početnim podacima na desnom kraju integracionog segmenta u zavisnosti od koraka mreže. Jasno je vidljivo koliko se proračuni za nestabilne i stabilne šeme dramatično razlikuju jedni od drugih. Pomoću ovog programa možete provjeriti vrijednost praga parametra s= 0,5: at s < 0,5 схема неустойчива, при s³ 0,5 - stabilno.

Listing_No.5

% Program za proračun za nestabilnu šemu na

%sigma=0,25 i prema stabilnoj šemi na sigma=0,75

%čišćenje radnog prostora

%definiraj konstantu jednačine u"=alfa*u

%definisati vrednosti sigma=0.25; 0,75

sigm=0,25:0,5:0,75;

za s=1:dužina(sigm)

%definirajte početnu vrijednost koraka mreže

x=0:h:1; N=dužina(x);

%odrediti poremećaje početnih podataka

dy(1)=1e-6; dy(2)=1e-6;

% vršimo proračun smetnje početne

% podataka na desnom kraju segmenta integracije

dy(n+1)=(2+(alfa*h-1)/sigma)*dy(n)+...

(1/sigma-1)*dy(n-1);

% zapamtite smetnju na desnom kraju i

%mrežni razmak

deltay(i)=dy(N);

%nacrtati graf zavisnosti smetnje od

%desna granica od koraka mreže

plot(korak,deltay);

Slika 11. Grafovi zavisnosti poremećaja pri proračunu prema
dijagram (53) na desnoj granici koraka mreže h

Šema razlike(51¢), (52¢) stabilan, ako rješenje sistema diferencijskih jednačina kontinuirano ovisi o ulaznim podacima j, c i ova zavisnost je uniformna u odnosu na korak mreže. Pojasnimo kontinuiranu zavisnost. To znači da za bilo koga e> 0 postoji takav d(e), nezavisno od h, Šta

, (56)

Ako je shema razlike (51¢), (52¢) linearna, tada rješenje razlike linearno ovisi o ulaznim podacima. U ovom slučaju to možemo pretpostaviti d(e) = e/(M + M 1), gdje M, M 1 - neke nenegativne veličine nezavisne od h. Kao rezultat toga, uvjet stabilnosti za linearne diferencialne sheme može se zapisati kao:

Kontinuirana zavisnost rješenja razlike od j pozvao stabilnost na desnoj strani, i od c - stabilnost prema graničnim podacima.

U budućnosti ćemo razmotriti dvoslojne diferentne šeme, tj. takve šeme koje sadrže jedan poznati i jedan novi, nepoznati sloj.

Dvoslojna razlika shema se zove jednolično stabilan po početnim podacima, ako pri odabiru početnih podataka iz bilo kojeg sloja t * (t 0 £ t * < T) razlika shema je stabilna u odnosu na njih, a stabilnost je uniformna u odnosu na t*. Za linearne šeme, uslov uniformne stabilnosti se može zapisati u obliku

gdje je konstanta K ne zavisi od t* I h, - rješenja razlika sheme A h y = j sa početnim podacima i sa istom desnom stranom.

Dovoljan znak uniformne stabilnosti. Za ujednačenu stabilnost prema početnim podacima dovoljno je da za sve m sprovedeno

Dokaz. Uvjet (60) znači da ako dođe do greške na nekom sloju dy, tada pri prelasku na sljedeći sloj norma poremećaja || dy|| povećava za najviše (1 + St) £ e C t jednom. Prema (59), pri pomicanju iz sloja t*po sloju t potrebno m = (t - t *)/t vremenskim koracima, tj. greška se povećava ne više od . Kao rezultat imamo

što prema definiciji u (59) znači uniformnu stabilnost prema početnim podacima.

Teorema. Neka je dvoslojna razlika shema A h y = j je uniformno stabilan u odnosu na početne podatke i takav je da ako dva različita rješenja A h y k = j k jednaki su na nekom sloju, tj. , tada sljedeći sloj zadovoljava relaciju

Gdje a= konst. Tada je šema razlike stabilna na desnoj strani.

Dokaz. Osim rješenja y Razmotrimo rješenje koje odgovara poremećenoj desnoj strani. U nastavku ćemo pretpostaviti da . Ovo se može pretpostaviti, jer Proučava se stabilnost na desnoj strani.