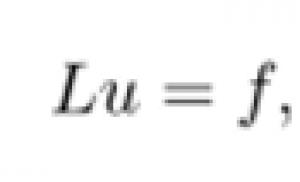Funkcionalna serija. Funkcionalni nizovi, područje konvergencije, uniformna konvergencija, Weierstrassov znak, svojstva uniformno konvergentnih funkcionalnih nizova, Uniformna konvergencija funkcionalnog niza i njegova svojstva

Područje konvergencije Funkcionalni niz je niz čiji su članovi funkcije / definirane na određenom skupu E brojevne ose. Na primjer, članovi niza su definirani na intervalu, a članovi niza definirani su na intervalu. Za funkcionalni niz (1) se kaže da konvergira u tački Ho € E ako konvergira. konvergencija Weierstrassov test Svojstva uniformno konvergentnih funkcionalnih nizova numeričkih nizova Ako red (1) konvergira u svakoj tački x skupa D C E i divergira u svakoj tački koja ne pripada skupu D, onda kažu da red konvergira na skupu D , a D se naziva područjem konvergencije reda. Za niz (1) se kaže da je apsolutno konvergentan na skupu D ako niz konvergira na ovom skupu. U slučaju konvergencije niza (1) na skupu D, njegov zbir S će biti funkcija definirana na D. Područje konvergencije nekih funkcionalnih nizova može se pronaći korištenjem poznatih dovoljnih kriterija uspostavljenih za nizove s pozitivnim članovima, na primjer, Dapambertov test, Cauchyjev test. Primjer 1. Naći područje konvergencije niza M Pošto numerički niz konvergira za p > 1 i divergira za p ^ 1, onda, uz pretpostavku p - Igx, dobijamo ovaj niz. koji će konvergirati na Igx > T, tj. ako je x > 10, a divergiraju kada je Igx ^ 1, tj. u 0< х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > Red 0 divergira, pošto je A =. Divergencija serije na x = 0 je očigledna. Primjer 3. Odrediti područje konvergencije reda.. Članovi datog reda su definirani i kontinuirani na skupu. Koristeći kriterij Kosh i, nalazimo za bilo koji. Posljedično, niz se divergira za sve vrijednosti x. Označimo sa Sn(x) n-ti parcijalni zbir funkcionalnog niza (1). Ako ovaj niz konvergira na skupu D i njegov zbir je jednak 5(g), onda se može predstaviti u obliku gdje je zbir niza koji konvergira na skupu D koji se naziva n-ti ostatak funkcionalnog niza ( 1). Za sve vrijednosti x € D vrijedi relacija i stoga. to jest, ostatak Rn(x) konvergentnog niza teži nuli kao n oo, bez obzira na x 6 D. Uniformna konvergencija Među svim konvergentnim funkcionalnim redovima, takozvani uniformno konvergentni nizovi igraju važnu ulogu. Neka je dan niz funkcija konvergentan na skupu D čiji je zbir jednak S(x). Uzmimo njegov n-ti parcijalni zbir Definicija. Funkcionalni nizovi FUNKCIONALNI NIZ Područje konvergencije Uniformna konvergencija Weierstrassov test Za svojstva uniformno konvergentnih funkcionalnih nizova kaže se da su uniformno konvergentne na skupu PS1) ako za bilo koji broj e > O postoji broj Γ > O takav da nejednakost vrijedi za sve brojeve n > N i za sve x iz skupa fI. Komentar. Ovdje je broj N isti za sve x € Yu, tj. ne zavisi od z, već zavisi od izbora broja e, pa pišemo N = N(e). Ujednačena konvergencija funkcionalnog niza £ /n(®) funkciji S(x) na skupu ft često se označava na sljedeći način: Definicija uniformne konvergencije niza /n(x) na skupu ft može se napisati još ukratko koristeći logičke simbole: Hajde da objasnimo geometrijski značenje funkcionalnog opsega uniformne konvergencije. Uzmimo segment [a, 6] kao skup ft i konstruirajmo grafove funkcija. Nejednakost |, koja vrijedi za brojeve n > N i za sve a; G [a, b], može se zapisati u sljedećem obliku: Dobijene nejednakosti pokazuju da će grafovi svih funkcija y = 5n(x) sa brojevima n > N biti u potpunosti sadržani unutar £-pojasa ograničenog krivuljama y = S(x) - e i y = 5(g) + e (slika 1). Primjer 1 ravnomjerno konvergira na intervalu. Ovaj niz je naizmjeničan predznakom, zadovoljava uslove Leibnizovog kriterija za bilo koje x € [-1,1] i stoga konvergira na intervalu (-1,1). Neka je S(x ) je njegov zbir, a Sn (x) je njegov n-ti parcijalni zbir. Ostatak niza u apsolutnoj vrijednosti ne prelazi apsolutnu vrijednost njegovog prvog člana: i budući da uzmimo bilo koje e. Tada će nejednakost | biti zadovoljena ako. Odavde nalazimo da je n > \. Ako uzmemo broj (ovdje [a] označava najveći cijeli broj koji ne prelazi a), onda je nejednakost | e će vrijediti za sve brojeve n > N i za sve x € [-1,1). To znači da ovaj niz ravnomjerno konvergira na intervalu [-1,1). I. Nije svaki funkcionalni niz konvergentan na skupu D uniformno konvergentan na primjeru 2. Pokažimo da red konvergira na intervalu, ali ne uniformno. 4 Izračunajmo n-ti parcijalni zbir £„(*) niza. Imamo Gdje se ovaj niz konvergira na segmentu i njegovom zbiru ako je apsolutna vrijednost razlike S(x) - 5„(x) (ostatak niza) jednaka. Uzmimo broj e takav da. Neka Razriješimo nejednakost u odnosu na n. Imamo odakle (pošto i kada se dijeli sa Inx, predznak nejednakosti se mijenja u suprotan). Nejednakost će biti zadovoljena kada. Dakle, postoji takav broj N(e) nezavisno od x da je nejednakost zadovoljena za svaki) za sve x iz segmenta odjednom. , ne postoji. Zamijenimo li segment 0 manjim segmentom, pri čemu će na potonjem ovaj niz ravnomjerno konvergirati funkciji S0. U stvari, za, a samim tim i za sve x odjednom §3. Weierstrassov test Dovoljan test za uniformnu konvergenciju funkcionalnog niza dat je Weierstrassovom teoremom. Teorema 1 (Weierstrassov test). Neka za sve x iz skupa Q članovi funkcionalnog niza u apsolutnoj vrijednosti ne prelaze odgovarajuće članove konvergentnog numeričkog niza P = 1 sa pozitivnim članovima, odnosno za sve x € Q. Tada je funkcionalni niz (1 ) na skupu P konvergira apsolutno i uniformno . A Tek pošto, prema uslovima teoreme, članovi reda (1) zadovoljavaju uslov (3) na čitavom skupu Q, onda u poređenju niz 2 \fn(x)\ konvergira za bilo koje x € I, i , prema tome, niz (1) apsolutno konvergira na P. Dokažimo uniformnu konvergenciju reda (1). Neka Sn(x) i an označavaju parcijalne sume redova (1) i (2), respektivno. Uzmimo bilo koji (proizvoljno mali) broj e > 0. Tada iz konvergencije niza brojeva (2) slijedi postojanje broja N = N(e) takvog da je, prema tome, -e za sve brojeve n > N (e) i za sve xbP , tj. niz (1) ravnomerno konvergira na skupu P. Napomena. Brojčani niz (2) se često naziva majoriranjem ili majorantom za funkcionalni niz (1). Primjer 1. Ispitati uniformnu konvergenciju niza.Nejednakost vrijedi za sve. i za sve. Brojevi se konvergiraju. Na osnovu Weierstrassovog kriterija, funkcionalni nizovi koji se razmatraju konvergiraju apsolutno i jednolično na cijeloj osi. Primjer 2. Ispitati ravnomjernu konvergenciju niza.Članovi niza su definirani i kontinuirani na intervalu [-2,2|. Budući da na intervalu [-2,2) za bilo koji prirodni broj n, dakle, nejednakost vrijedi za. Budući da se brojevni niz konvergira, onda, prema Weierstrassovom kriteriju, originalni funkcionalni niz konvergira apsolutno i jednolično na segmentu. Komentar. Funkcionalni niz (1) može ravnomerno konvergirati na skup Piv u slučaju kada nema numeričkog majorantnog niza (2), odnosno Weierstrassov kriterijum je samo dovoljan kriterijum za uniformnu konvergenciju, ali nije neophodan. Primjer. Kao što je gore prikazano (primjer), red konvergira ravnomjerno na segmentu 1-1,1]. Međutim, za njega ne postoji majorantni konvergentni broj (2). U stvari, za sve prirodne n i za sve x € [-1,1) nejednakost je zadovoljena i jednakost se postiže kada. Dakle, članovi željenog majorantnog reda (2) svakako moraju zadovoljiti uslov ali brojčani niz FUNKCIONALNI NIZ Područje konvergencije Uniformna konvergencija Weierstrassov test Svojstva uniformno konvergentnog funkcionalnog niza divergira. To znači da će se niz £op također razići. Svojstva uniformno konvergentnih funkcionalnih nizova Uniformno konvergentni funkcionalni nizovi imaju niz važnih svojstava. Teorema 2. Ako se svi članovi niza koji uniformno konvergiraju na intervalu [a, b] pomnože istom funkcijom d(x) ograničenom na [a, 6], tada će rezultirajući funkcionalni niz konvergirati uniformno na. Neka na intervalu [a, b\ niz £ fn(x) jednoliko konvergira funkciji 5(x), a funkcija d(x) je ograničena, tj. postoji konstanta C > 0 takva da je Po definiciji uniformne konvergencije niza za bilo koji broj e > 0 postoji broj N takav da će za sve n > N i za sve x € [a, b] nejednakost biti zadovoljena gdje je 5n(ar) parcijalni zbir serija koja se razmatra. Stoga ćemo ga imati za svakoga. red konvergira uniformno na [a, b| na funkciju Teorem 3. Neka su svi članovi fn(x) funkcionalnog niza neprekidni i nizovi jednoliko konvergiraju na intervalu [a, b\. Tada je zbir S(x) niza kontinuiran na ovom intervalu. M Uzmimo dvije proizvoljne tačke ig + Ax na segmentu [o, b]. Budući da se ovaj niz ravnomjerno konvergira na intervalu [a, b], onda za bilo koji broj e > O postoji broj N = N(e) takav da su za sve i > N zadovoljene nejednakosti gdje su 5„(g) parcijalne sume serije fn (x). Ove parcijalne sume 5n(x) su kontinuirane na intervalu [a, 6] kao sume konačnog broja funkcija fn(x) kontinuirane na [a, 6]. Stoga, za fiksni broj br > N(e) i dati broj e, postoji broj 6 = 6(e) > 0 takav da će za prirast Ax koji zadovoljava uvjet | vrijediti nejednakost: Prirast AS od zbir S(x) se može predstaviti u sljedećem obliku: gdje. Uzimajući u obzir nejednakosti (1) i (2), za priraštaje Ax koji zadovoljavaju uslov |, dobijamo To znači da je zbir Six) kontinuiran u tački x. Pošto je x proizvoljna tačka segmenta [a, 6], onda je 5(x) kontinuirano na |a, 6|. Komentar. Funkcionalni niz čiji su članovi kontinuirani na intervalu [a, 6), ali koji neravnomjerno konvergira na (a, 6], može imati diskontinuiranu funkciju kao zbir. Primjer 1. Razmotrimo funkcionalni niz na intervalu |0,1 ). Izračunajmo njen n-ti parcijalni zbir, pa je diskontinuiran na segmentu, iako su članovi reda na njemu kontinuirani. Na osnovu dokazane teoreme, ovaj niz nije uniformno konvergentan na intervalu. Primjer 2. Razmotrimo niz Kao što je gore prikazano, ovaj niz konvergira na, red će konvergirati jednolično prema Weierstrassovom testu, budući da se 1 i brojevni niz konvergiraju. Prema tome, za bilo koje x > 1 zbir ovog niza je kontinuiran. Komentar. Funkcija se zove Riemannova funkcija (ova funkcija igra veliku ulogu u teoriji brojeva). Teorema 4 (o integraciji funkcionalnog niza po član). Neka su svi članovi fn(x) niza neprekidni i nizovi jednoliko konvergiraju na intervalu [a, b] funkciji S(x). Tada vrijedi jednakost: Zbog kontinuiteta funkcija f„(x) i uniformne konvergencije ovog niza na intervalu [a, 6], njegov zbir 5(x) je kontinuiran i, prema tome, integrabilan na . Razmotrimo razliku. Iz uniformne konvergencije niza na [o, b] slijedi da za bilo koje e > 0 postoji broj N(e) > 0 takav da je za sve brojeve n > N(e) i za sve x € [a, 6] nejednakost će biti zadovoljena Ako red fn(0 nije uniformno konvergentan, onda se, općenito govoreći, ne može integrirati pojam po član, tj. Teorema 5 (o diferencijaciji po članu funkcionalnog niza) Neka svi članovi konvergentnog niza 00 imaju neprekidne izvode i niz sastavljen od ovih izvoda, konvergira jednoliko na intervalu [a, b]. Tada je u bilo kojoj tački jednakost tačna, tj. ovaj niz se može diferencirati članom M Uzmimo bilo koje dvije tačke. Tada ćemo, na osnovu teoreme 4, imati Funkcija o-(x) je kontinuirana kao zbir uniformno konvergentnog niza kontinuiranih funkcija. Dakle, razlikovanjem jednakosti dobijamo Vježbe Pronađite područja konvergencije ovih funkcionalnih redova: Koristeći Weierstrassov test, dokažite uniformnu konvergenciju ovih funkcionalnih redova na naznačenim intervalima:

Funkcionalni raspon se naziva formalno pisani izraz

u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ... , (1)

Gdje u1 (x), u 2 (x), u 3 (x), ..., u n ( x), ... - niz funkcija iz nezavisne varijable x.

Skraćeni zapis funkcionalnog niza sa sigmom: .

Primjeri funkcionalnih serija uključuju :

(2)

(3)

Davanje nezavisne varijable x neku vrednost x0 i zamjenom u funkcionalni niz (1) dobijamo numerički niz

u1 (x 0 ) + u 2 (x 0 ) + u 3 (x 0 ) + ... + u n ( x 0 ) + ...

Ako rezultirajuća numerička serija konvergira, tada se kaže da funkcionalni niz (1) konvergira za x = x0 ; ako se divergira, ono što se kaže je da se niz (1) divergira na x = x0 .

Primjer 1. Istražiti konvergenciju funkcionalnog niza(2) na vrijednostima x= 1 i x = - 1 .
Rješenje. At x= 1 dobijamo niz brojeva

koji konvergira prema Leibnizovom kriterijumu. At x= - 1 dobijamo niz brojeva

,

koji divergira kao proizvod divergentnog harmonijskog niza za – 1. Dakle, niz (2) konvergira na x= 1 i divergira na x = - 1 .

Ako se takva provjera konvergencije funkcionalnog niza (1) izvrši u odnosu na sve vrijednosti nezavisne varijable iz domene definicije njenih članova, tada će se točke ovog domena podijeliti u dva skupa: za vrijednosti x, uzet u jednom od njih, niz (1) konvergira, au drugom divergira.

Skup vrijednosti nezavisne varijable kod koje se funkcionalni niz konvergira naziva se njegovim područje konvergencije .

Primjer 2. Naći područje konvergencije funkcionalnog niza

Rješenje. Članovi niza su definirani na cijeloj brojevnoj pravoj i čine geometrijsku progresiju sa nazivnikom q= grijeh x. Stoga se red konvergira ako

i odstupa ako

(vrijednosti nisu moguće). Ali za vrijednosti i za druge vrijednosti x. Dakle, red konvergira za sve vrijednosti x, osim . Područje njegove konvergencije je cijela brojevna prava, sa izuzetkom ovih tačaka.

Primjer 3. Pronađite područje konvergencije funkcionalnog niza

Rješenje. Članovi niza čine geometrijsku progresiju sa nazivnikom q=ln x. Stoga, serija konvergira ako , ili , odakle . Ovo je područje konvergencije ove serije.

Primjer 4. Istražiti konvergenciju funkcionalnog niza

Rješenje. Uzmimo proizvoljnu vrijednost. Sa ovom vrijednošću dobijamo niz brojeva

(*)

Nađimo granicu njegovog zajedničkog pojma

Posljedično, niz (*) divergira za proizvoljno odabrano, tj. po bilo kojoj vrijednosti x. Njegovo područje konvergencije je prazan skup.

Uniformna konvergencija funkcionalnog niza i njegova svojstva

Pređimo na koncept uniformna konvergencija funkcionalnog niza . Neka s(x) je zbir ove serije i sn ( x) - suma n prvi članovi ove serije. Funkcionalni raspon u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ... naziva se uniformno konvergentnim na intervalu [ a, b] , ako je za bilo koji proizvoljno mali broj ε > 0 postoji takav broj N to pred svima n ≥ N nejednakost će biti ispunjena

|s(x) − s n ( x)| < ε

za bilo koga x iz segmenta [ a, b] .

Gore navedeno svojstvo može se geometrijski ilustrovati na sljedeći način.

Razmotrimo graf funkcije y = s(x) . Konstruirajmo traku širine 2 oko ove krive ε n, odnosno konstruisaćemo krive y = s(x) + ε n I y = s(x) − ε n(na slici ispod su zelene).

Onda za bilo koje ε n graf funkcije sn ( x) će u potpunosti ležati u traci koja se razmatra. Ista traka će sadržavati grafove svih narednih parcijalnih suma.

Svaki konvergentni funkcionalni niz koji nema gore opisanu karakteristiku je neravnomjerno konvergentan.

Razmotrimo još jedno svojstvo uniformno konvergentnih funkcionalnih nizova:

zbir niza kontinuiranih funkcija koje ravnomjerno konvergiraju na određenom intervalu [ a, b] , postoji funkcija kontinuirana na ovom intervalu.

Primjer 5. Odrediti da li je zbir funkcionalnog niza kontinuiran

Rješenje. Hajde da nađemo sumu n prvi članovi ove serije:

Ako x> 0, onda

,

Ako x < 0 , то

Ako x= 0, onda

I zbog toga .

Naše istraživanje je pokazalo da je zbir ovog niza diskontinuirana funkcija. Njegov grafikon je prikazan na donjoj slici.

Weierstrassov test za uniformnu konvergenciju funkcionalnih redova

Mi pristupamo Weierstrassovom kriteriju kroz koncept majorizabilnost funkcionalnih serija . Funkcionalni raspon

u1 (x) + u 2 (x) + u 3 (x) + ... + u n ( x) + ...

Lukhov Yu.P. Bilješke sa predavanja iz više matematike. Predavanje br. 42 5

Predavanje 42

PREDMET: Funkcionalna serija

Plan.

1. Funkcionalna serija. Region konvergencije.
2. Uniformna konvergencija. Weierstrass sign.
3. Svojstva uniformno konvergentnih redova: kontinuitet zbira nizova, integracija po članu i diferencijacija.
4. Power series. Abelova teorema. Područje konvergencije potencijskog reda. Radijus konvergencije.
5. Osnovna svojstva stepena redova: uniformna konvergencija, kontinuitet i beskonačna diferencijabilnost zbira. Integracija i diferencijacija redova stepena po član.

Funkcionalna serija. Region konvergencije

Definicija 40.1. Beskonačna količina funkcija

u 1 (x) + u 2 (x) +…+ u n (x) +…, (40.1)

gdje je u n (x) = f (x, n), naziva se funkcionalni raspon.

Ako navedete određenu numeričku vrijednost X , serija (40.1) će se pretvoriti u niz brojeva, ovisno o izboru vrijednosti X takav niz može konvergirati ili divergirati. Samo konvergentni redovi imaju praktičnu vrijednost, pa je važno odrediti te vrijednosti X , pri čemu funkcionalni niz postaje konvergentan broj brojeva.

Definicija 40.2. Višestruka značenja X , kada se zamijene u funkcionalni niz (40.1) dobije se konvergentni numerički niz, naziva sepodručje konvergencijefunkcionalni raspon.

Definicija 40.3. funkcija s(x), definiran u području konvergencije niza, koji za svaku vrijednost X iz područja konvergencije jednak je zbiru odgovarajuće numeričke serije dobijene iz (40.1) za datu vrijednost x se zove zbir funkcionalnog niza.

Primjer. Nađimo područje konvergencije i zbir funkcionalnog niza

1 + x + x² +…+ x n +…

Kada | x | ≥ 1 stoga se odgovarajući brojčani nizovi razilaze. Ako

| x | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

Prema tome, opseg konvergencije niza je interval (-1, 1), a njegov zbir ima naznačeni oblik.

Komentar . Baš kao i za niz brojeva, možete uvesti koncept parcijalnog zbroja funkcionalnog niza:

s n = 1 + x + x² +…+ x n

i ostatak serije: r n = s s n .

Uniformna konvergencija funkcionalnog niza

Hajde da prvo definišemo koncept uniformne konvergencije niza brojeva.

Definicija 40.4. Funkcionalni niz fn(x) se poziva ravnomjerno konvergiraju funkciji f na skupu X ako je i

Napomena 1. Označit ćemo uobičajenu konvergenciju funkcionalnog niza i uniformnu konvergenciju sa .

Napomena 2 . Zapazimo još jednom fundamentalnu razliku između uniformne konvergencije i obične konvergencije: u slučaju obične konvergencije, za odabranu vrijednost ε, za svaku postoji tvoj broj N, za koje na n>N vrijedi nejednakost:

U ovom slučaju može se ispostaviti da je za dati ε opći broj N, osiguravajući ispunjenje ove nejednakosti za bilo koji X , nemoguće. U slučaju uniformne konvergencije, takav broj N, zajedničko za sve x, postoji.

Definirajmo sada koncept uniformne konvergencije funkcionalnog niza. Pošto svaki niz odgovara nizu njegovih parcijalnih suma, uniformna konvergencija niza je određena kroz uniformnu konvergenciju ovog niza:

Definicija 40.5. Funkcionalni niz se zoveuniformno konvergentan na skupu X, ako je na X niz njegovih parcijalnih suma konvergira jednoliko.

Weierstrass sign

Teorema 40.1. Ako se brojevni niz konvergira i za svakoga i za svakoga n = 1, 2,... nejednakost je zadovoljena tada red konvergira apsolutno i uniformno na skupu X.

Dokaz.

Za bilo koje ε > 0 s postoji takav broj N, zbog čega

Za ostatke r n serija procena je fer

Dakle, red konvergira jednolično.

Komentar. Obično se zove postupak za izbor niza brojeva koji ispunjava uslove iz teoreme 40.1 majorizacija , i sama ova serija majorante za dati funkcionalni opseg.

Primjer. Za funkcionalnu seriju majoranta za bilo koju vrijednost X je konvergentan niz sa pozitivnim predznakom. Prema tome, originalni niz ravnomjerno konvergira na (-∞, +∞).

Svojstva uniformno konvergentnih redova

Teorema 40.2. Ako funkcije u n (x) su neprekidne na i red konvergira ravnomjerno na X, tada njegov zbir s (x) je takođe kontinuirano u jednoj tački x 0 .

Dokaz.

Odaberimo ε > 0. Dakle, postoji takav broj n 0 to

- zbir konačnog broja kontinuiranih funkcija, daklekontinuirano u jednoj tački x 0 . Stoga postoji δ > 0 takav da tada dobijamo:

To jest, funkcija s (x) je kontinuirana na x = x 0.

Teorema 40.3. Neka su funkcije u n (x) kontinuirano na intervalu [ a, b ] i niz ravnomjerno konvergira na ovom segmentu. Tada se niz također ravnomjerno konvergira na [ a , b ] i (40.2)

(odnosno, pod uslovima teoreme, nizovi se mogu integrisati pojam po član).

Dokaz.

Prema teoremi 40.2 funkcija s(x) = kontinuirano na [a, b ] i, prema tome, na njemu je integrabilna, odnosno postoji integral na lijevoj strani jednakosti (40.2). Pokažimo da niz uniformno konvergira funkciji

Označimo

Tada za bilo koje ε postoji takav broj N, što za n > N

To znači da red konvergira jednolično, a njegov zbir je jednak σ ( x) = .

Teorema je dokazana.

Teorema 40.4. Neka su funkcije u n (x) se kontinuirano diferenciraju na intervalu [ a, b ] i niz sastavljen od njihovih derivata:

(40.3)

konvergira jednoliko na [ a, b ]. Zatim, ako se niz konvergira barem u jednoj tački, tada se konvergira ravnomjerno kroz [ a , b ], njegov zbir s (x )= je kontinuirano diferencibilna funkcija i

(serija se može diferencirati pojam po pojam).

Dokaz.

Definirajmo funkciju σ( X ) Kako. Prema teoremi 40.3, niz (40.3) se može integrirati pojam po član:

Niz na desnoj strani ove jednakosti ravnomjerno konvergira u [ a, b ] prema teoremi 40.3. Ali prema uslovima teoreme, niz brojeva konvergira, dakle, niz takođe konvergira jednolično. Tada funkcija σ( t ) je zbir uniformno konvergentnog niza kontinuiranih funkcija na [ a, b ] i stoga je sam po sebi kontinuiran. Tada je funkcija kontinuirano diferencibilna na [ a, b ], i to je ono što je trebalo dokazati.

Definicija 41.1. Power series naziva se funkcionalni niz oblika

(41.1)

Komentar. Korištenje zamjene x x 0 = t niz (41.1) se može svesti na oblik, pa je dovoljno dokazati sva svojstva nizova stepena za nizove oblika

(41.2)

Teorema 41.1 (Abelova 1. teorema).Ako se niz stepena (41.2) konvergira na x = x 0, tada za bilo koje x: | x |< | x 0 | niz (41.2) apsolutno konvergira. Ako se niz (41.2) divergira na x = x 0, onda se razlikuje za bilo koje x: | x | > | x 0 |.

Dokaz.

Ako se niz konvergira, postoji konstanta c > 0:

Posljedično, i serija za | x |<| x 0 | konvergira jer je zbir beskonačno opadajuće geometrijske progresije. To znači da je serija na | x |<| x 0 | apsolutno se poklapa.

Ako je poznato da niz (41.2) divergira na x = x 0 , onda ne može konvergirati na | x | > | x 0 | , pošto bi iz onoga što je prethodno dokazano sledilo da konvergira u tački x 0 .

Dakle, ako nađete najveći broj x 0 > 0 tako da (41.2) konvergira za x = x 0, tada će područje konvergencije ovog niza, kao što slijedi iz Abelove teoreme, biti interval (- x 0, x 0 ), moguće uključujući jednu ili obje granice.

Definicija 41.2. Poziva se broj R ≥ 0 radijus konvergencijestepena reda (41.2), ako se ovaj niz konvergira i divergira. Interval (- R, R) se zove interval konvergencije serija (41.2).

Primjeri.

1. Da bismo proučavali apsolutnu konvergenciju niza, primjenjujemo d’Alembertov test: . Dakle, niz konvergira samo kada X = 0, a njegov radijus konvergencije je 0: R = 0.
2. Koristeći isti d'Alembertov test, možemo pokazati da niz konvergira za bilo koji x, tj
3. Za niz koji koristi d'Alembertov kriterijum dobijamo:

Stoga, za 1< x < 1 ряд сходится, при

x< -1 и x > 1 se razilazi. At X = 1 dobijamo harmonijski niz, koji, kao što je poznato, divergira i kada X = -1 niz konvergira uslovno prema Leibnizovom kriterijumu. Dakle, radijus konvergencije niza koji se razmatra R = 1, a interval konvergencije je [-1, 1).

Formule za određivanje radijusa konvergencije stepena niza.

1. d'Alembertova formula.

Razmotrimo niz stepena i na njega primijenimo d'Alembertov kriterij: da bi red konvergirao, potrebno je da ako postoji, tada je područje konvergencije određeno nejednakošću, tj.

- (41.3)

• d'Alembertova formulaza izračunavanje radijusa konvergencije.

1. Cauchy-Hadamard formula.

Koristeći radikalni Cauchyjev test i razmišljajući na sličan način, nalazimo da možemo definirati područje konvergencije niza stepena kao skup rješenja nejednakosti, podložno postojanju ove granice, i, shodno tome, pronaći drugu formulu za radijus konvergencije:

(41.4)

• Cauchy-Hadamard formula.

Svojstva potencijskog reda.

Teorema 41.2 (Abelova 2. teorema). Ako je R poluprečnik konvergencije reda (41.2) i ovaj niz konvergira na x = R , tada konvergira jednoliko na intervalu (- R, R).

Dokaz.

Pozitivan niz konvergira prema teoremi 41.1. Prema tome, niz (41.2) konvergira jednolično u intervalu [-ρ, ρ] prema teoremi 40.1. Iz izbora ρ slijedi da je interval uniformne konvergencije (- R, R ), što je trebalo dokazati.

Zaključak 1 . Na svakom segmentu koji u potpunosti leži unutar intervala konvergencije, zbir niza (41.2) je kontinuirana funkcija.

Dokaz.

Članovi niza (41.2) su kontinuirane funkcije, a red konvergira jednolično na intervalu koji se razmatra. Tada kontinuitet njegovog zbira slijedi iz teoreme 40.2.

Zaključak 2. Ako granice integracije α, β leže unutar intervala konvergencije niza stepena, tada je integral zbira reda jednak zbiru integrala članova reda:

(41.5)

Dokaz ove tvrdnje slijedi iz teoreme 40.3.

Teorema 41.3. Ako serija (41.2) ima interval konvergencije (- R, R), zatim serija

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +…+ na n x n- 1 +…, (41.6)

dobijen diferencijacijom po članu reda (41.2) ima isti interval konvergencije (- R, R). Gde

φ΄(x) = s΄ (x) za | x |< R , (41.7)

to jest, unutar intervala konvergencije, derivacija sume niza stepena jednaka je zbiru niza dobijenog njegovom diferencijacijom po članu.

Dokaz.

Odaberimo ρ: 0< ρ < R и ζ: ρ < ζ < R . Tada niz konvergira, dakle, ako| x | ≤ ρ, onda

Dakle, članovi niza (41.6) su manji po apsolutnoj vrijednosti od članova niza pozitivnih predznaka, koji konvergiraju prema D’Alembertovom kriteriju:

to jest, to je majorant za niz (41.6) za Dakle, niz (41.6) konvergira jednolično na [-ρ, ρ]. Dakle, prema teoremi 40.4, jednakost (41.7) je tačna. Iz izbora ρ slijedi da niz (41.6) konvergira u bilo kojoj unutrašnjoj tački intervala (- R, R).

Dokažimo da izvan ovog intervala niz (41.6) divergira. Zaista, ako se konvergira na x 1 > R , zatim, integrirajući ga pojam po član na intervalu (0, x 2 ), R< x 2 < x 1 , dobili bismo da red (41.2) konvergira u tački x 2 , što je u suprotnosti sa uslovima teoreme. Dakle, teorema je u potpunosti dokazana.

Komentar . Serija (41.6), zauzvrat, može se diferencirati pojam po član i ova operacija se može izvesti koliko god puta se želi.

zaključak: ako se niz stepena konvergira na intervalu (- R, R ), tada je njen zbir funkcija koja ima derivate bilo kojeg reda unutar intervala konvergencije, od kojih je svaki zbir niza dobivenog iz originalnog pomoću diferencijacije član po član odgovarajući broj puta; Štaviše, interval konvergencije za niz derivacija bilo kog reda je (- R, R).

Departman za informatiku i višu matematiku KSPU

Tema 2. Funkcionalne serije. Power series

2.1. Funkcionalna serija

Do sada smo razmatrali serije čiji su članovi bili brojevi. Pređimo sada na proučavanje nizova čiji su članovi funkcije.

Funkcionalni raspon zove red

čiji su članovi funkcije istog argumenta definiranog na istom skupu E.

Na primjer,

1.
;

2.
;

Ako damo argument X neku numeričku vrednost
,
, tada dobijamo niz brojeva

koji mogu konvergirati (konvergirati apsolutno) ili divergirati.

Ako na
rezultirajući niz brojeva konvergira, a zatim tačka
pozvaotačka konvergencije funkcionalni raspon. Skup svih tačaka konvergencije se zovepodručje konvergencije funkcionalni raspon. Označimo područje konvergencije X, očigledno,
.

Ako se za numeričke nizove sa pozitivnim predznakom postavlja pitanje: "Da li se niz konvergira ili divergira?", za naizmjenične nizove postavlja se pitanje: "Da li konvergira, uslovno ili apsolutno, ili divergira?", tada se za funkcionalni niz glavno pitanje je: „Konvergirati (konvergirati apsolutno) u čemu X?».

Funkcionalni raspon
uspostavlja zakon prema kojem svaka vrijednost argumenta
,
, dodjeljuje se broj jednak zbiru niza brojeva
. Dakle, na setu X funkcija je specificirana
, koji se zove zbir funkcionalnog niza.

Primjer 16.

Pronađite područje konvergencije funkcionalnog niza

.

Rješenje.

Neka X je fiksni broj, onda se ovaj niz može smatrati nizom brojeva sa pozitivnim predznakom kada
i naizmjenično u
.

Napravimo niz apsolutnih vrijednosti članova ove serije:

za bilo koju vrijednost X ova granica je manja od jedan, što znači da ovaj niz konvergira, i to apsolutno (pošto smo proučavali niz apsolutnih vrijednosti članova niza) na cijeloj numeričkoj osi.

Dakle, oblast apsolutne konvergencije je skup
.

Primjer 17.

Pronađite područje konvergencije funkcionalnog niza
.

Rješenje.

Neka X– fiksni broj,
, onda se ovaj niz može smatrati nizom brojeva sa pozitivnim predznakom kada
i naizmjenično u
.

Razmotrimo niz apsolutnih vrijednosti članova ove serije:

i primijeniti D'Alembertov test na njega.

Prema DAlembertovom testu, niz konvergira ako je granična vrijednost manja od jedan, tj. ovaj niz će se konvergirati ako
.

Rješavanjem ove nejednakosti dobijamo:


.

Dakle, kada , niz sastavljen od apsolutnih vrijednosti članova ovog niza konvergira, što znači da se originalni niz apsolutno konvergira, a kada
ova serija se razlikuje.

At
nizovi mogu konvergirati ili divergirati, jer za ove vrijednosti X granična vrijednost je jednaka jedinici. Stoga dodatno ispitujemo konvergenciju određenog broja tačaka
I
.

Zamjena u ovom redu
, dobijamo niz brojeva
, za koji se zna da je harmonijski divergentni niz, što znači tačka
– tačka divergencije date serije.

At
dobijamo niz naizmeničnih brojeva

za koje je poznato da konvergira uslovno (vidi primjer 15), što znači tačka
– tačka uslovne konvergencije serije.

Dakle, područje konvergencije ovog niza je , a serija konvergira apsolutno na .

Funkcionalni raspon

pozvaomajorized u nekom području varijacije x, ako postoji takav konvergentni niz pozitivnog predznaka

,

da je za sve x iz ovog regiona uslov zadovoljen
at
. Red
pozvaomajorante.

Drugim riječima, nizom dominira ako svaki od njegovih članova nije veći po apsolutnoj vrijednosti od odgovarajućeg člana nekog konvergentnog pozitivnog niza.

Na primjer, serija

je majorizacija za bilo koje X, jer za svakoga X relacija važi

at
,

i red , kao što je poznato, je konvergentna.

TeoremaWeierstrass

Serija koja je specijalizirana za određenu regiju apsolutno konvergira u tu regiju.

Razmotrimo, na primjer, funkcionalni niz
. Ova serija je majorizirana kada
, od kada
članovi serije ne prelaze odgovarajuće članove pozitivne serije . Prema tome, prema Weierstrassovom teoremu, razmatrani funkcionalni nizovi apsolutno konvergiraju za
.

2.2. Power series. Abelova teorema. Područje konvergencije stepena niza

Među nizom funkcionalnih nizova najvažniji su sa stajališta praktične primjene energetski i trigonometrijski redovi. Pogledajmo ove serije detaljnije.

Power series po stepenima
naziva se funkcionalni niz oblika

Gdje – neki fiksni broj,
– brojevi koji se nazivaju koeficijenti serije.

At
dobijamo niz stepena po stepenu X, koji ima oblik

.

Radi jednostavnosti, razmotrićemo redove stepena u stepenima X, pošto je iz takvog niza lako dobiti niz po stepenu
, zamjenjujući umjesto toga X izraz
.

Jednostavnost i važnost klase stepena niza je prvenstveno zbog činjenice da je parcijalni zbir stepena reda

je polinom - funkcija čija su svojstva dobro proučena i čije se vrijednosti lako izračunavaju koristeći samo aritmetičke operacije.

Kako su redovi stepena poseban slučaj funkcionalnog niza, potrebno je i za njih pronaći područje konvergencije. Za razliku od domene konvergencije proizvoljnog funkcionalnog niza, koji može biti skup bilo kojeg oblika, domen konvergencije stepena niza ima potpuno određen oblik. O tome govori sljedeća teorema.

TeoremaAbel.

Ako je snaga serije
konvergira po nekoj vrijednosti
, tada konvergira, apsolutno, za sve vrijednosti x koje zadovoljavaju uvjet
. Ako se niz stepena divergira za neku vrijednost
, onda se divergira za vrijednosti koje zadovoljavaju uslov
.

Iz Abelove teoreme slijedi da Sve tačke konvergencije stepena redova po stepenu X lociran od početka koordinata ne dalje od bilo koje tačke divergencije. Očigledno je da tačke konvergencije ispunjavaju određeni jaz u centru ishodišta. vrijedi teorema o području konvergencije stepena reda.

Teorema.

Za bilo koju seriju snage
postoji brojR (R>0)tako da za sve x koji leže unutar intervala
, red konvergira apsolutno i za sve x koji leže izvan intervala
, serija se razilazi.

BrojRpozvaoradijus konvergencije potencijskog niza i intervala
– interval konvergencije redovi stepena u stepenu x.

Imajte na umu da teorema ne govori ništa o konvergenciji niza na krajevima intervala konvergencije, tj. u tačkama
. U tim se točkama različiti nizovi snaga ponašaju različito: nizovi se mogu konvergirati (apsolutno ili uslovno) ili mogu divergirati. Stoga, konvergenciju serije u ovim tačkama treba direktno provjeriti po definiciji.

U posebnim slučajevima, radijus konvergencije niza može biti jednak nuli ili beskonačnosti. Ako
, zatim red po stepenu X konvergira u samo jednoj tački
; ako
, tada se niz stepena konvergira na cijeloj brojevnoj osi.

Obratimo još jednom pažnju na činjenicu da je red
po stepenima
može se svesti na niz stepena
koristeći zamjenu
. Ako je red
konvergira na
, tj. Za
, tada nakon obrnute zamjene dobivamo

 ili
.

Dakle, interval konvergencije stepena reda
izgleda kao
. Tačka pozvao centar konvergencije. Radi jasnoće, uobičajeno je da se interval konvergencije prikaže na numeričkoj osi (slika 1)

Dakle, oblast konvergencije se sastoji od intervala konvergencije u koji se mogu dodati tačke
, ako se red konvergira u ovim tačkama. Interval konvergencije se može naći direktnom primjenom DAlembertovog testa ili Cauchyjevog radikalnog testa na niz sastavljen od apsolutnih vrijednosti članova datog niza.

Primjer 18.

Pronađite područje konvergencije niza
.

Rješenje.

Ova serija je niz po moćima X, tj.
. Razmotrimo niz sastavljen od apsolutnih vrijednosti članova ovog niza i koristimo DAlembertov znak.

Niz će konvergirati ako je granična vrijednost manja od 1, tj.

, gdje
.

Dakle, interval konvergencije ovog niza
, radijus konvergencije
.

Istražujemo konvergenciju niza na krajevima intervala, u tačkama
. Zamjena vrijednosti u ovu seriju
, dobili smo seriju

.

Rezultirajući niz je harmonijski divergentni niz, dakle, u tački
serija se razilazi, što znači tačku
nije uključen u regiju konvergencije.

At
dobijamo naizmeničnu seriju

,

koji je uslovno konvergentan (primjer 15), otuda i poenta
– tačka konvergencije (uslovna).

Dakle, oblast konvergencije serije
, i u točki
Niz konvergira uslovno, au drugim tačkama konvergira apsolutno.

Rezoniranje korišteno za rješavanje primjera može se dati opći karakter.

Razmotrite redove snage

Sastavimo niz apsolutnih vrijednosti članova niza i na njega primijenimo D'Alembertov znak.

Ako postoji (konačna ili beskonačna) granica, tada će prema uslovu konvergencije D'Alembertovog kriterija, niz konvergirati ako

,

,

.

Dakle, iz definicije intervala i radijusa konvergencije, imamo

Koristeći radikalni Cauchyjev test i razmišljajući na sličan način, možemo dobiti još jednu formulu za pronalaženje radijusa konvergencije

Primjer 19

Rješenje.

Serija je niz po moćima X. Da bismo pronašli interval konvergencije, izračunavamo radijus konvergencije koristeći gornju formulu. Za dati niz, formula za numerički koeficijent ima oblik

, Onda

dakle,

Jer R = , tada red konvergira (i apsolutno) za sve vrijednosti X, one. region konvergencije X (–; +).

Imajte na umu da bi bilo moguće pronaći područje konvergencije bez upotrebe formula, već direktnom primjenom Alembertovog kriterija:

Budući da vrijednost granice ne ovisi o X i manji od 1, tada red konvergira za sve vrijednosti X, one. at X(-;+).

Primjer 20

Pronađite područje konvergencije niza

1!(X+5)+2!(X + 5) 2 +3!(X + 5) 3 +... + P!(X + 5) P +...

Rješenje .

x + 5), one. centar konvergencije X 0 = - 5. Numerički koeficijent serije A P = n!.

Nađimo radijus konvergencije serije

.

Dakle, interval konvergencije se sastoji od jedne tačke - centra intervala konvergencije x = - 5.

Primjer 21

Pronađite područje konvergencije niza
.

Rješenje.

Ova serija je niz stepena po stepenu ( X–2), one.

centar konvergencije X 0 = 2. Imajte na umu da je serija pozitivan predznak za bilo koji fiksni X, budući da je izraz ( X- 2) podignut na stepen 2 P. Primijenimo radikalni Cauchyjev test na seriju.

Niz će konvergirati ako je granična vrijednost manja od 1, tj.

,
,
,

To znači da je radijus konvergencije
, zatim integral konvergencije

,
.

Dakle, serija konvergira apsolutno na X
. Imajte na umu da je integral konvergencije simetričan u odnosu na centar konvergencije X O = 2.

Proučimo konvergenciju niza na krajevima intervala konvergencije.

Believing
, dobijamo numerički niz sa pozitivnim predznakom

Koristimo neophodan kriterijum za konvergenciju:

stoga se brojevni niz divergira i tačka
je tačka razilaženja. Imajte na umu da smo prilikom izračunavanja granice koristili drugu izuzetnu granicu.

Believing
, dobijamo isti niz brojeva (provjerite sami!), što znači tačku
takođe nije uključen u interval konvergencije.

Dakle, oblast apsolutne konvergencije ovog niza X
.

2.3. Svojstva konvergentnih redova stepena

Znamo da je konačan zbir kontinuiranih funkcija kontinuiran; zbir diferencijabilnih funkcija je diferencibilan, a derivacija sume jednaka je zbiru izvoda; konačni zbir se može integrirati pojam po član.

Ispostavilo se da za "beskonačne sume" funkcija - nizove funkcija - svojstva ne vrijede u opštem slučaju.

Na primjer, razmotrite funkcionalnu seriju

Očigledno je da su svi članovi niza kontinuirane funkcije. Nađimo područje konvergencije ovog niza i njegov zbir. Da bismo to učinili, nalazimo parcijalne sume niza

zatim zbir serije

Dakle, iznos S(X) datog niza, kao granica niza parcijalnih suma, postoji i konačan je za X (-1;1), To znači da je ovaj interval područje konvergencije niza. Štaviše, njegov zbir je diskontinuirana funkcija, budući da

Dakle, ovaj primjer pokazuje da u opštem slučaju svojstva konačnih suma nemaju analoga za beskonačne sume - nizove. Međutim, za poseban slučaj funkcionalnog niza - niz stepena - svojstva sume su slična svojstvima konačnih suma.

– možda kompleks neće ispasti tako složen;) I naslov ovog članka je također neiskren - serije o kojima će se danas raspravljati nisu složene, već „rijetke zemlje“. Međutim, ni vanredni studenti nisu imuni na njih, te stoga ovu naizgled dodatnu lekciju treba shvatiti s najvećom ozbiljnošću. Na kraju krajeva, nakon što ga razradite, moći ćete se nositi sa gotovo svakom "zvijeri"!

Počnimo s klasicima žanra:

Primjer 1

Prvo, imajte na umu da ovo NIJE power serija (podsjećam te da izgleda). I, drugo, ovdje vrijednost odmah upada u oči, koja se očito ne može uključiti u područje konvergencije serije. I ovo je već mali uspjeh studije!

Ali ipak, kako postići veliki uspjeh? Požurim da vas zadovoljim - takve serije mogu se riješiti na potpuno isti način kao moć– na osnovu d’Alembertovog ili radikalnog Cauchyjevog znaka!

Rješenje: vrijednost nije unutar raspona konvergencije serije. Ovo je značajna činjenica i mora se napomenuti!

Osnovni algoritam radi standardno. Koristeći d'Alembertov kriterij, nalazimo interval konvergencije niza:

Serija konvergira na . Pomjerimo modul gore:

Odmah provjerimo "lošu" tačku: vrijednost nije uključena u raspon konvergencije serije.

Hajde da ispitamo konvergenciju niza na "unutrašnjim" krajevima intervala:
ako onda
ako onda

Oba niza brojeva se razilaze jer neophodan znak konvergencije.

Odgovori: područje konvergencije:

Uradimo malu analitičku provjeru. Zamijenimo neku vrijednost iz desnog intervala u funkcionalni niz, na primjer:
– konvergira dalje d'Alambertov znak.

U slučaju zamjene vrijednosti iz lijevog intervala, također se dobijaju konvergentni nizovi:
ako onda .

I konačno, ako , onda serija – zaista se razilazi.

Par jednostavnih primjera za zagrijavanje:

Primjer 2

Pronađite područje konvergencije funkcionalnog niza

Primjer 3

Pronađite područje konvergencije funkcionalnog niza

Budite posebno dobri u ophođenju sa "novim" modul– desiće se 100.500 puta danas!

Kratka rješenja i odgovori na kraju lekcije.

Čini se da su korišteni algoritmi univerzalni i bez problema, ali u stvari to nije slučaj - za mnoge funkcionalne serije često "skliznu" i čak dovode do pogrešnih zaključaka (Takođe ću razmotriti takve primjere).

Neravnine počinju već na nivou interpretacije rezultata: uzmite u obzir, na primjer, seriju. Ovdje smo u limitu (provjerite sami), a u teoriji morate dati odgovor da se niz konvergira u jednoj tački. Međutim, poenta je „izigrana“, što znači da se naš „pacijent“ svuda razilazi!

A za seriju, “očigledno” Cauchyjevo rješenje ne daje baš ništa:
– za BILO KOJU vrijednost “x”.

I postavlja se pitanje šta učiniti? Koristimo metodu kojoj će biti posvećen glavni dio lekcije! Može se formulisati na sljedeći način:

Direktna analiza brojevnih nizova za različite vrijednosti

U stvari, to smo već počeli raditi u primjeru 1. Prvo, ispitujemo određeni „X“ i odgovarajući broj brojeva. Treba uzeti vrijednost:
– rezultirajući niz brojeva se razilazi.

I to odmah navodi na misao: šta ako se ista stvar dogodi na drugim mjestima?
Hajde da proverimo neophodan znak konvergencije niza Za proizvoljno značenja:

Poenta je uzeta u obzir gore, za sve ostale "X" Mi ćemo se dogovoriti standardno druga divna granica:

Zaključak: niz se razilazi duž cijele brojevne prave

A ovo rješenje je najizvodljivija opcija!

U praksi, funkcionalne serije se često moraju porediti generalizovani harmonijski niz :

Primjer 4

Rješenje: pre svega, da se pozabavimo domenu definicije: u ovom slučaju radikalni izraz mora biti striktno pozitivan, a osim toga, svi članovi serije moraju postojati, počevši od 1. Iz ovoga proizilazi da:
. Sa ovim vrijednostima dobijaju se uslovno konvergentni nizovi:
itd.

Drugi "x" nisu prikladni, pa, na primjer, kada dobijemo nelegalan slučaj gdje prva dva člana serije ne postoje.

Sve je to dobro, sve je jasno, ali ostaje još jedno važno pitanje - kako ispravno formalizirati odluku? Predlažem shemu koja se kolokvijalno može nazvati "prevođenjem strelica" u niz brojeva:

Hajde da razmotrimo proizvoljno značenje i proučavanje konvergencije brojevnih nizova. Rutina Leibnizov znak:

1) Ova serija je naizmjenična.

2) – članovi serije smanjuju modul. Svaki sljedeći član serije je manji po modulu od prethodnog: , što znači da je smanjenje monotono.

Zaključak: niz konvergira prema Leibnizovom kriteriju. Kao što je već napomenuto, konvergencija je ovdje uslovna - iz razloga što je serija – razilazi se.

Samo tako - uredno i korektno! Jer iza “alfe” smo spretno sakrili sve dozvoljene nizove brojeva.

Odgovori: funkcionalni niz postoji i konvergira uslovno na .

Sličan primjer za nezavisno rješenje:

Primjer 5

Istražiti konvergenciju funkcionalnog niza

Okvirni uzorak završnog zadatka na kraju lekcije.

Toliko o vašoj "radnoj hipotezi"! – funkcionalni niz konvergira na intervalu!

2) Sa simetričnim intervalom sve je transparentno, razmotrite proizvoljno vrijednosti i dobijamo: – apsolutno konvergentan broj brojeva.

3) I na kraju, „sredina“. I ovdje je zgodno istaknuti dvije praznine.

Razmatramo proizvoljno vrijednost iz intervala i dobijamo niz brojeva:

! Opet - ako je teško , zamijenite određeni broj, na primjer . Međutim... hteli ste teškoće =)

Urađeno za sve vrijednosti "en" , znači:
- dakle, prema poređenje serija konvergira zajedno sa beskonačno opadajućom progresijom.

Za sve vrijednosti "x" iz intervala dobijamo – apsolutno konvergentni niz brojeva.

Svi "X-ovi" su istraženi, nema više "X-ova"!

Odgovori: raspon konvergencije serije:

Moram reći, neočekivani rezultat! A treba dodati i da će upotreba d'Alembertovih ili Cauchyjevih znakova ovdje definitivno dovesti u zabludu!

Direktna procjena je "akrobatika" matematičke analize, ali za to je, naravno, potrebno iskustvo, au nekim slučajevima čak i intuicija.

Ili će možda neko naći lakši način? Pisati! Inače, ima presedana - nekoliko puta su čitaoci predlagali racionalnija rješenja, a ja sam ih sa zadovoljstvom objavljivao.

Uspješno sletanje :)

Primjer 11

Pronađite područje konvergencije funkcionalnog niza

Moja verzija rješenja je vrlo bliska.

Dodatni hardcore se može naći u Odjeljak VI (redovi) Kuznjecova kolekcija (Zadaci 11-13). Na internetu postoje gotova rješenja, ali ovdje ste mi potrebni upozoriti– mnoge od njih su nepotpune, netačne ili čak potpuno pogrešne. I, usput rečeno, to je bio jedan od razloga zašto je nastao ovaj članak.

Hajde da sumiramo tri lekcije i sistematizujmo naše alate. dakle:

Da biste pronašli interval(e) konvergencije niza funkcija, možete koristiti:

1) D'Alembertov ili Cauchyjev znak. A ako red nije smireno– pokazujemo povećan oprez kada analiziramo rezultat dobijen direktnom zamjenom različitih vrijednosti.

2) Weierstrassov test za uniformnu konvergenciju. Ne zaboravi!

3) Poređenje sa standardnim brojevnim nizovima– pravila u opštem slučaju.

Onda ispitati krajeve pronađenih intervala (ako je potrebno) i dobijamo oblast konvergencije reda.

Sada imate na raspolaganju prilično ozbiljan arsenal koji će vam omogućiti da se nosite s gotovo svim tematskim zadatkom.

Želim ti uspjeh!

Rješenja i odgovori:

Primjer 2: Rješenje: vrijednost nije unutar raspona konvergencije serije.
Koristimo d'Alambertov znak:


Serija se konvergira na:

Dakle, intervali konvergencije funkcionalnog niza: .
Hajde da istražimo konvergenciju niza na krajnjim tačkama:
ako onda ;
ako onda .
Oba niza brojeva se razilaze, jer potreban kriterijum konvergencije nije ispunjen.

Odgovori : područje konvergencije: