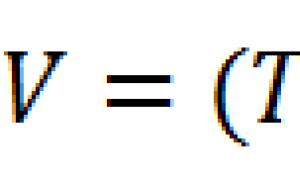Coordonate generalizate, forțe generalizate. Forța generalizată a unui sistem cu un grad de libertate Forța generalizată

Luați în considerare un sistem mecanic cu conexiuni ideale. Fie  forțele active ale sistemului. Să dăm sistemului mecanic o deplasare virtuală și să calculăm munca elementară a forțelor sistemului asupra acestei deplasări:

.

Folosind egalitatea (17.2), exprimăm variația
raza vectoriala puncte M k prin variatii
coordonate generalizate:

prin urmare,

. (17.6)

Să schimbăm ordinea însumării în egalitate (17.6):

. (17.7)

Notați în expresie (17.7)

. (17.8)

.

Forțe generalizate Q j sunt coeficienții pentru variații ale coordonatelor generalizate în exprimarea lucrului elementar al forțelor sistemului.

În funcţie de dimensiunea variaţiilor coordonatelor generalizate
forţe generalizate Q j poate avea dimensiunea forței, momentului etc.

Metode de calcul a forțelor generalizate

Luați în considerare trei moduri de a calcula forțele generalizate.

1. Determinarea forțelor generalizate prin formula de bază(17.8)

. (17.9)

Formula (17.9) este rar folosită în practică. La rezolvarea problemelor, se folosește adesea a doua metodă.

2. Metoda de „înghețare” a coordonatelor generalizate.

Să dăm unui sistem mecanic o deplasare virtuală astfel încât toate variațiile coordonatelor generalizate cu excepția
egal cu zero:

Calculăm munca pentru această mișcare
toate forțele active aplicate sistemului

.

Prin definiție, multiplicatorul de variație
egală cu prima forță generalizată Q 1 .

și definiți a doua forță generalizată Q 2, calculând munca virtuală a tuturor forțelor sistemului

.

Calculăm toate celelalte forțe generalizate ale sistemului într-un mod similar.

3. Cazul unui câmp de forță potențial.

Să presupunem că energia potențială a sistemului mecanic este cunoscută

Atunci
și prin formula (32.8)

Principiul deplasărilor virtuale ale staticii în coordonate generalizate

Conform principiului deplasărilor virtuale ale staticii pentru echilibrul unui sistem cu constrângeri holonomice, staționare de limitare ideală, este necesar și suficient ca condiția

la viteze inițiale zero.

Trecând la coordonate generalizate, obținem

. (17.11)

Deoarece variațiile coordonatelor generalizate sunt independente, egalitatea la zero a expresiei (17.11) este posibilă numai dacă toți coeficienții variațiilor coordonatelor generalizate sunt egali cu zero:

În acest fel, pentru ca un sistem mecanic cu constrângeri ideale, holonomice, staționare și restrictive să fie în echilibru, este necesar și suficient ca toate forțele generalizate ale sistemului să fie egale cu zero (la viteze inițiale zero ale sistemului).

Ecuații Lagrange în coordonate generalizate (ecuații Lagrange de al doilea fel)

Ecuațiile Lagrange sunt derivate din ecuația generală a dinamicii prin înlocuirea deplasărilor virtuale cu expresiile lor în termeni de variații ale coordonatelor generalizate. Ele reprezintă un sistem de ecuații diferențiale ale mișcării unui sistem mecanic în coordonate generalizate:

. (17.13)

Unde
 viteze generalizate,

T energia cinetică a sistemului, prezentată în funcţie de coordonate generalizate şi viteze generalizate

Q j forţe generalizate.

Numărul de ecuații ale sistemului (17.13) este determinat de numărul de grade de libertate și nu depinde de numărul de corpuri incluse în sistem. Cu constrângeri ideale, doar forțele active vor intra în partea dreaptă a ecuațiilor. Dacă conexiunile sunt imperfecte, atunci reacțiile lor ar trebui atribuite forțelor active.

În cazul forțelor potențiale care acționează asupra unui sistem mecanic, ecuațiile (17.13) iau forma

.

Dacă introducem funcția Lagrange L = T  P, ținând cont de faptul că energia potențială nu depinde de vitezele generalizate, obținem ecuațiile Lagrange de al doilea fel pentru cazul forțelor potențiale în forma următoare

.

Când compilați ecuațiile Lagrange de al doilea fel, trebuie să faceți următoarele:

Stabiliți numărul de grade de libertate ale sistemului mecanic și selectați coordonatele generalizate ale acestuia.

Alcătuiți o expresie pentru energia cinetică a sistemului și reprezentați-o în funcție de coordonatele generalizate și de viteze generalizate.

Folosind metodele prezentate mai sus, găsiți forțele active generalizate ale sistemului.

Efectuați toate operațiile de diferențiere necesare în ecuațiile Lagrange.

Exemplu.

Unde J z momentul de inerţie al corpului faţă de axa de rotaţie z,
 viteza unghiulară a corpului.

3. Să definim forța generalizată. Să dăm corpului o deplasare virtuală  și să calculăm munca virtuală a tuturor forțelor active ale sistemului:

Prin urmare, Q = M z momentul principal al forţelor active ale sistemului faţă de axa de rotaţie a corpului.

4. Să efectuăm operații de diferențiere în ecuația Lagrange

: (17.14)

. (17.15)

Înlocuirea egalităților (17.15) în ecuația (173

14) obținem ecuația diferențială a mișcării de rotație a corpului

.

1. Forța generalizată poate fi calculată prin formula (227), care o determină, i.e.

2. Forțele generalizate pot fi calculate ca coeficienți pentru variațiile corespunzătoare ale coordonatelor generalizate în expresia pentru lucrul elementar (226 "), i.e.

3. Cea mai convenabilă metodă de calcul a forțelor generalizate, care se obține din (226 ""), dacă sistemului i se spune o astfel de posibilă deplasare la care se modifică doar o coordonată generalizată, în timp ce celelalte nu se modifică. Deci dacă, și restul , apoi din (179 ") avem

.

Indicele indică faptul că suma muncii elementare se calculează pe o posibilă deplasare, în care doar coordonatele se modifică (variază). Dacă coordonata variabilă este, atunci

. (227")

Condiții de echilibru pentru un sistem de forțe în termeni de forțe generalizate

Condiții de echilibru a sistemului sunt derivate din principiul posibilelor deplasări. Ele se aplică sistemelor pentru care acest principiu este adevărat: pentru echilibrul unui sistem mecanic supus unor constrângeri holonomice, staţionare, ideale şi neeliberatoare, în momentul în care vitezele tuturor punctelor sistemului sunt egale cu zero, este necesar şi suficient ca toate forţele generalizate să fie egale cu zero.

. (228")

Ecuația generală a dinamicii

Ecuația generală a dinamicii pentru un sistem cu orice constrângeri (principiul combinat d'Alembert-Lagrange sau ecuația generală a mecanicii):

, (229)

unde este forța activă aplicată celui de-al-lea punct al sistemului; - puterea reacției legăturilor; - forța de inerție a unui punct; - posibila miscare.

În cazul echilibrului sistemului, când toate forțele de inerție ale punctelor sistemului devin zero, acesta se transformă în principiul posibilelor deplasări. De obicei, este utilizat pentru sistemele cu constrângeri ideale pentru care condiția

În acest caz, (229) ia una dintre formele:

,

,

. (230)

În acest fel, conform ecuației generale a dinamicii, în orice moment al mișcării unui sistem cu constrângeri ideale, suma muncii elementare a tuturor forțelor active și a forțelor de inerție ale punctelor sistemului este egală cu zero la orice posibilă deplasare a sistemului. permise de constrângeri.

Ecuația generală a dinamicii poate avea alte forme echivalente. Extinderea produsului scalar al vectorilor, acesta poate fi exprimat ca

unde sunt coordonatele celui de-al-lea punct al sistemului. Ținând cont de faptul că proiecțiile forțelor de inerție pe axele de coordonate prin proiecțiile accelerațiilor pe aceste axe sunt exprimate prin relațiile

,

ecuaţiei generale a dinamicii i se poate da forma

În această formă se numește ecuaţia generală a dinamicii în formă analitică.

Atunci când se utilizează ecuația generală a dinamicii, este necesar să se poată calcula munca elementară a forțelor de inerție ale sistemului asupra posibilelor deplasări. Pentru aceasta, se aplică formulele corespunzătoare pentru munca elementară, obținute pentru forțele convenționale. Să luăm în considerare aplicarea lor pentru forțele inerțiale ale unui corp rigid în cazuri particulare de mișcare a acestuia.

Când mergi înainte. În acest caz, corpul are trei grade de libertate și, datorită constrângerilor impuse, poate efectua doar mișcare de translație. Posibilele deplasări ale corpului, care permit conexiuni, sunt de asemenea translaționale.

Forțele de inerție în timpul mișcării de translație sunt reduse la rezultantă ... Pentru suma muncii elementare a forțelor de inerție asupra posibilei deplasări de translație a corpului, obținem

unde este deplasarea posibilă a centrului de masă și a oricărui punct al corpului, deoarece deplasarea posibilă de translație în toate punctele corpului este aceeași: accelerațiile sunt și ele aceleași, i.e.

Când un corp rigid se rotește în jurul unei axe fixe. Corpul în acest caz are un grad de libertate. Se poate roti în jurul unei axe fixe. Mișcarea posibilă, care este permisă de constrângerile impuse, este și o rotație a corpului printr-un unghi elementar în jurul unei axe fixe.

Forțele de inerție, reduse la un punct pe axa de rotație, sunt reduse la vectorul principal și momentul principal. Vectorul principal al forțelor inerțiale este aplicat unui punct fix, iar munca sa elementară asupra unei posibile deplasări este zero. În momentul principal al forțelor de inerție, lucrul elementar care nu este egal cu zero va fi efectuat numai prin proiecția sa pe axa de rotație. Astfel, pentru suma muncii forțelor inerțiale asupra deplasării posibile considerate, avem

,

dacă unghiul este raportat în direcția săgeții arcului accelerației unghiulare.

Cu mișcare plată. Constrângerile impuse unui corp rigid, în acest caz, permit doar o posibilă deplasare plană. În cazul general, ea constă într-o posibilă mișcare de translație împreună cu polul, în spatele căruia alegem centrul de masă, și rotație printr-un unghi elementar în jurul unei axe care trece prin centrul de masă și perpendicular pe plan, paralel cu care corpul poate efectua o mișcare plană.

În mecanica analitică, împreună cu conceptul de forță ca mărime vectorială care caracterizează efectul asupra unui anumit corp de la alte corpuri materiale, conceptul de putere generalizată... Pentru determinare putere generalizată luați în considerare munca virtuală a forțelor aplicate punctelor sistemului.

Dacă i se impune un sistem mecanic cu constrângeri holonomice h are conexiuni s = 3n-h grade de libertate , atunci se determină poziţia acestui sistem ( i = s)

coordonate generalizate și (2.11) : Conform (2.13), (2.14) deplasarea virtuală k - al-lea punct

(2.13)

(2.14)

Înlocuind (2.14): în formula pentru munca virtuală a forțelor

(2.24), obținem

Cantitatea scalară = (2.26)

sunt numite putere generalizată corespunzător i-a coordonata generalizata.

Puterea generalizatăcorespunzătoare i-a-a coordonată generalizată, se numește valoare egală cu un multiplicator cu o variație a unei coordonate generalizate date în expresia muncii virtuale a forțelor care acționează asupra unui sistem mecanic.

Lucrare virtuală determinat din

¾ setați forțele active, independente de constrângeri și

¾ reacții ale conexiunilor (dacă conexiunile nu sunt ideale, atunci pentru a rezolva problema este necesară setarea suplimentară a dependenței fizice T j din N j, ( T j este, de regulă, forţe de frecare sau momente de rezistenţă la frecare la rulare, pe care ştim să le determinăm).

În general forta generalizata este o funcție de coordonate generalizate, viteze ale punctelor sistemului și timp. Din definiţie rezultă că forta generalizata¾ valoare scalară care depinde de coordonatele generalizate selectate pentru sistemul mecanic dat. Aceasta înseamnă că atunci când se modifică setul de coordonate generalizate care determină poziția sistemului dat și forţe generalizate.

Exemplul 2.10. Pentru un disc cu o rază r si masa m, care se rostogolește fără alunecare pe un plan înclinat (Figura 2.9), poate fi luată ca o coordonată generalizată:

¾ fie q = s¾ deplasarea centrului de masă al discului,

Orice q= j este unghiul de rotație al discului. Dacă neglijăm rezistența la rulare, atunci:

¾ în primul caz putere generalizată voi

Orez. 2.9 Q s = mg sina și

¾ în al doilea caz ¾ Q j = mg r cosa.

Coordonata generalizată determină și unitatea de măsură a corespondentei forta generalizata. Din expresie (2.25)

(2.27)

rezultă că unitatea de măsură putere generalizată este egal cu unitatea de măsură a muncii împărțită la unitatea de măsură a coordonatei generalizate.

Dacă ca o coordonată generalizată q a accepta q = s¾ mutarea unui punct, apoi unitatea de măsură putere generalizată Q s ¾ va [newton] ,

Dacă, însă, ca q= j ¾ se va lua unghiul de rotație (în radiani) al corpului, apoi unitatea de măsură putere generalizată Q j ¾ va fi [ newton metru].

Fig. 71

Fig. 70

Fig. 69

Poziția punctelor mecanismului manivelă (Fig. 70) poate fi determinată prin setarea unghiului manivelei sau distanței s determinarea poziţiei toboganului V(la ).

Poziţia pendulului sferic (Fig. 71) se determină prin specificarea a doi parametri, unghiuri şi.

Numărul minim de coordonate generalizate independente, care sunt suficiente pentru a determina complet și fără ambiguitate poziția tuturor punctelor sistemului, se numește numărul de grade de libertate acest sistem.

În general, mai multe coordonate generalizate pot fi atribuite oricărui sistem material. De exemplu, pentru mecanismul manivelei (Fig. 70), sunt indicate două coordonate generalizate și. Dar asta nu înseamnă că mecanismul are două grade de libertate, deoarece o coordonată poate fi determinată prin cealaltă:

Dar pendulul (Fig. 71) are două grade de libertate, deoarece poziţia sa este determinată de două coordonate generalizate independente. Apropo, dacă lungimea pendulului se modifică, atunci pentru a determina poziția punctului M mai este necesar un parametru - coordonata generalizata l, lungimea firului. Iar pendulul va avea trei grade de libertate.

Coordonatele generalizate în cazul general vor fi notate prin literă q.

Lasă sistemul material să aibă s grade de libertate. Poziția sa este determinată de coordonatele generalizate: q 1 , q 2 , q 3 ,…, q k,…, q s. .

Este ușor de verificat dacă coordonatele carteziene n punctele sistemului pot fi definite ca funcții de coordonate generalizate și timp:

Deci pendulul (Fig. 71) are coordonatele punctului M

există funcții de coordonate l, și, și timp t, dacă l = l (t).

În consecință, vectorul rază al punctelor sistemului poate fi definit ca o funcție a coordonatelor generalizate și a timpului:

Pentru fiecare coordonată generalizată se poate calcula forța generalizată corespunzătoare Q k.

Calculul se face conform acestei reguli.

Pentru a determina forța generalizată Q k corespunzătoare coordonatei generalizate q k, este necesar să se acorde o creștere acestei coordonate (mărește coordonatele cu această valoare), lăsând toate celelalte coordonate neschimbate, se calculează suma muncii tuturor forțelor aplicate sistemului asupra deplasărilor corespunzătoare de puncte și se împarte la increment a coordonatei:

unde este deplasarea i-al-lea punct al sistemului, obtinut prin schimbare k– Coordonata generalizată.

Forța generalizată se determină folosind munca elementară. Prin urmare, această forță poate fi calculată diferit:

Și deoarece există o creștere a vectorului rază datorită creșterii coordonatei cu restul coordonatelor și timpului neschimbat t, relația poate fi definită ca o derivată parțială. Atunci

unde coordonatele punctelor sunt funcții ale coordonatelor generalizate (5).

Dacă sistemul este conservator, adică mișcarea are loc sub acțiunea forțelor câmpului potențial, ale căror proiecții, unde și coordonatele punctelor sunt funcții de coordonate generalizate, atunci

Forța generalizată a unui sistem conservator este o derivată parțială a energiei potențiale de-a lungul coordonatei generalizate corespunzătoare cu semnul minus.

Desigur, atunci când se calculează această forță generalizată, energia potențială ar trebui determinată în funcție de coordonatele generalizate

P = P ( q 1 , q 2 , q 3 ,…,q s).

Observatii.

Primul. La calcularea forțelor generalizate nu sunt luate în considerare reacțiile constrângerilor ideale.

Al doilea. Dimensiunea forței generalizate depinde de dimensiunea coordonatei generalizate. Deci, dacă dimensiunea [ q] - metru, apoi dimensiune

Nm / m = Newton dacă [ q] - radian, atunci = Nm; dacă [ q] = m 2, apoi etc.

Exemplul 23. Un inel alunecă de-a lungul unei tije care se balansează într-un plan vertical M greutate R(fig. 72). Considerăm că lanseta este lipsită de greutate. Să definim forțele generalizate.

Desigur, atunci când se calculează această forță generalizată, energia potențială ar trebui determinată în funcție de coordonatele generalizate

P = P ( q 1 , q 2 , q 3 ,…,q s).

Observatii.

Primul. La calcularea forțelor generalizate nu sunt luate în considerare reacțiile constrângerilor ideale.

Al doilea. Dimensiunea forței generalizate depinde de dimensiunea coordonatei generalizate. Deci, dacă dimensiunea [ q] - metru, apoi dimensiune

[Q] = Nm / m = Newton dacă [ q] - radian, atunci [Q] = Nm; dacă [ q] = m 2, apoi [Q] = H / m etc.

Exemplul 4. Un inel alunecă de-a lungul unei tije care se balansează într-un plan vertical M greutate R(fig. 10). Considerăm că lanseta este lipsită de greutate. Să definim forțele generalizate.

Fig. 10

Soluţie. Sistemul are două grade de libertate. Atribuirea a două coordonate generalizate sși .

Să găsim forța generalizată corespunzătoare coordonatei s. Oferim o creștere acestei coordonate, lăsând coordonatele neschimbate și calculând munca singurei forțe active R, obținem forța generalizată

Apoi creștem coordonatele prin setare s= const. Când bara este rotită printr-un unghi, punctul de aplicare al forței R, inel M, se va muta la. Forța generalizată se va dovedi

Deoarece sistemul este conservator, forțele generalizate pot fi găsite și folosind energia potențială. Primim și ... Se dovedește mult mai ușor.

Ecuații de echilibru ale lui Lagrange

Prin definiție (7), forțele generalizate , k = 1,2,3,…,s, Unde s- numărul de grade de libertate.

Dacă sistemul este în echilibru, atunci conform principiului posibilelor deplasări (1) ... Aici - deplasări permise de legături, posibile deplasări. Prin urmare, atunci când sistemul material este în echilibru, toate forțele sale generalizate sunt egale cu zero:

Q k= 0, (k=1,2,3,…, s). (10)

Aceste ecuații, ecuații de echilibru în coordonate generalizate sau Ecuații de echilibru Lagrange , permit rezolvarea problemelor de statică printr-o altă metodă.

Dacă sistemul este conservator, atunci. Prin urmare, într-o poziție de echilibru. Adică, în poziția de echilibru a unui astfel de sistem material, energia sa potențială este fie maximă, fie minimă, adică. funcția (q) are un extremum.

Acest lucru este evident din analiza celui mai simplu exemplu (Fig. 11). Energia potențială a mingii în poziție M 1 are un minim la poziție M 2 este maximul. Puteți vedea asta în poziție M 1 sold va fi stabil; gravidă M 2 - instabil.

Fig. 11

Echilibrul este considerat stabil dacă corpul în această poziție este transmis cu o viteză mică sau deplasat cu o distanță mică și aceste abateri nu vor crește în viitor.

Se poate dovedi (teorema Lagrange-Dirichlet) că dacă în poziţia de echilibru a unui sistem conservator energia sa potenţială are un minim, atunci această poziţie de echilibru este stabilă.

Pentru un sistem conservator cu un grad de libertate, condiția pentru energia potențială minimă și, prin urmare, stabilitatea poziției de echilibru, este determinată, de derivata a doua, de valoarea acesteia în poziția de echilibru,

Exemplul 5. Nucleu OA greutate R se poate roti într-un plan vertical în jurul unei axe O(fig. 12). Să găsim și să investigăm stabilitatea pozițiilor de echilibru.

Fig. 12

Soluţie. Tija are un grad de libertate. Coordonata generalizată este unghiul.

În ceea ce privește poziția inferioară, zero, energia potențială este P = Рh sau

În poziția de echilibru ar trebui să existe ... Prin urmare, avem două poziții de echilibru corespunzătoare unghiurilor și (pozițiilor OA 1 și OA 2). Să investigăm stabilitatea lor. Găsiți derivata a doua. Desigur, cu,. Poziția de echilibru este stabilă. La , ... A doua pozitie de echilibru este instabila. Rezultatele sunt clare.

Forțe de inerție generalizate.

Prin aceeași tehnică (8), prin care au fost calculate forțele generalizate Q k corespunzătoare forţelor active, date, se determină şi forţele generalizate S k corespunzătoare forțelor de inerție ale punctelor sistemului:

Și de când atunci

Câteva transformări matematice.

Evident,

Deoarece a qk = qk (t), (k = 1,2,3, ..., s), atunci

Prin urmare, derivata parțială a vitezei în raport cu

În plus, în ultimul termen (14), ordinea de diferențiere poate fi modificată:

Înlocuind (15) și (16) în (14) și apoi (14) în (13), obținem

Împărțind ultima sumă la doi și ținând cont că suma derivatelor este egală cu derivata sumei, obținem

unde este energia cinetică a sistemului, este viteza generalizată.

Ecuații Lagrange.

Prin definiție (7) și (12), forțele generalizate

Dar pe baza ecuației generale a dinamicii (3), partea dreaptă a egalității este egală cu zero. Și din moment ce totul ( k = 1,2,3,…,s) sunt diferite de zero, atunci. Înlocuind valoarea forței de inerție generalizate (17), obținem ecuația

Aceste ecuații sunt numite ecuații diferențiale de mișcare în coordonate generalizate, ecuații Lagrange de al doilea fel sau pur și simplu – Ecuații Lagrange.

Numărul acestor ecuații este egal cu numărul de grade de libertate ale sistemului material.

Dacă sistemul este conservator și se mișcă sub acțiunea forțelor câmpului potențial, atunci când forțele generalizate, ecuațiile Lagrange se pot scrie sub forma

Unde L = T- P este numit funcția Lagrange (se presupune că energia potențială P nu depinde de vitezele generalizate).

Adesea, atunci când se studiază mișcarea sistemelor materiale, se dovedește că unele coordonate generalizate q j nu sunt incluse în mod explicit în funcția Lagrange (sau în Tși P). Se numesc astfel de coordonate ciclic. Ecuațiile Lagrange corespunzătoare acestor coordonate sunt mai ușor de obținut.

Prima integrală a unor astfel de ecuații se găsește imediat. Se numește integrală ciclică:

Cercetări ulterioare și transformări ale ecuațiilor Lagrange fac obiectul unei secțiuni speciale de mecanică teoretică - „Mecanica analitică”.

Ecuațiile lui Lagrange au o serie de avantaje în comparație cu alte metode de studiere a mișcării sistemelor. Principalele avantaje: metoda de întocmire a ecuațiilor este aceeași în toate problemele, reacțiile conexiunilor ideale nu sunt luate în considerare la rezolvarea problemelor.

Și încă ceva - aceste ecuații pot fi folosite pentru a studia nu numai sistemele mecanice, ci și alte sisteme fizice (electrice, electromagnetice, optice etc.).

Exemplul 6. Să continuăm studiul mișcării inelului M pe o tijă de balansare (exemplul 4).

Coordonatele generalizate sunt atribuite - și s (Fig. 13). Forțele generalizate sunt definite: și .

Fig. 13

Soluţie. Energia cinetică a inelului Unde a și.

Compunem două ecuații Lagrange

atunci ecuațiile se obțin după cum urmează:

Au primit două ecuații diferențiale neliniare de ordinul doi, pentru a căror rezolvare sunt necesare metode speciale.

Exemplul 7. Să compunem ecuația diferențială a mișcării fasciculului AB, care se rostogolește fără alunecare pe o suprafață cilindrică (Fig. 14). Lungimea fasciculului AB = l, greutate - R.

În poziția de echilibru, fasciculul era situat orizontal și centrul de greutate CU era în vârful cilindrului. Fasciculul are un grad de libertate. Poziția sa este determinată de coordonatele generalizate - unghiul (Fig. 76).

Fig. 14

Soluţie. Sistemul este conservator. Prin urmare, compunem ecuația Lagrange folosind energia potențială P = mgh, calculată relativ la poziția orizontală. În punctul de tangență, există un centru instantaneu de viteze și (egal cu lungimea unui arc de cerc cu un unghi).

Prin urmare (vezi fig. 76) şi.

Energia cinetică (fasciul face o mișcare plan-paralelă)

Găsim derivatele necesare pentru ecuația și

Facem ecuația

sau, în sfârșit,

Întrebări de autotest

Ce se numește o posibilă mișcare a unui sistem mecanic neliber?

Cum sunt interconectate mișcările posibile și reale ale sistemului?

Ce conexiuni se numesc: a) staţionare; b) ideal?

Formulați principiul posibilelor deplasări. Notează-i expresia formulei.

Este posibil să se aplice principiul mișcărilor virtuale sistemelor cu conexiuni imperfecte?

Care sunt coordonatele generalizate ale unui sistem mecanic?

Care este numărul de grade de libertate ale unui sistem mecanic?

În ce caz, coordonatele carteziene ale punctelor sistemului depind nu numai de coordonatele generalizate, ci și de timp?

Ce se numește posibila mișcare a unui sistem mecanic?

Deplasările posibile depind de forțele care acționează asupra sistemului?

Ce conexiuni ale unui sistem mecanic se numesc ideale?

De ce o legătură de frecare nu este o legătură perfectă?

Cum este formulat principiul posibilelor deplasări?

Ce tipuri de ecuații de lucru pot avea?

De ce principiul posibilelor deplasări simplifică derivarea condițiilor pentru echilibrul forțelor aplicate sistemelor nelibere formate dintr-un număr mare de corpuri?

Cum sunt compuse ecuațiile de lucru pentru forțele care acționează asupra unui sistem mecanic cu mai multe grade de libertate?

Care este relația dintre forța motrice și forța de rezistență la cele mai simple mașini?

Cum este formulată regula de aur a mecanicii?

Cum se determină reacțiile de legătură folosind principiul posibilelor deplasări?

Ce fel de conexiuni se numesc holonomice?

Cum se numește numărul de grade de libertate ale unui sistem mecanic?

Care sunt coordonatele generalizate ale sistemului?

Câte coordonate generalizate are un sistem mecanic neliber?

Câte grade de libertate are un volan?

Ce se numește putere generalizată?

Notați formula care exprimă munca elementară completă a tuturor forțelor aplicate sistemului în coordonate generalizate.

Cum se determină dimensiunea forței generalizate?

Cum se calculează forțele generalizate în sistemele conservatoare?

Notați una dintre formulele care exprimă ecuația generală a dinamicii unui sistem cu constrângeri ideale. Care este sensul fizic al acestei ecuații?

Ce se numește forța generalizată a forțelor active aplicate sistemului?

Care este forța de inerție generalizată?

Formulați principiul d'Alembert în forțe generalizate.

Ce formă are ecuația generală a dinamicii?

Ce se numește forța generalizată corespunzătoare unei coordonate generalizate a sistemului și ce dimensiune are?

Cu ce ​​sunt egale reacțiile generalizate ale conexiunilor ideale?

Deduceți ecuația generală a dinamicii în forțe generalizate.

Ce formă sunt condițiile pentru echilibrul forțelor aplicate unui sistem mecanic obținut din ecuația generală a dinamicii în forțe generalizate?

Ce formule se folosesc pentru a exprima forțele generalizate prin proiecțiile forțelor pe axele fixe ale coordonatelor carteziene?

Cum sunt definite forțele generalizate în cazul forțelor conservatoare și neconservative?

Ce fel de conexiuni se numesc geometrice?

Dați o notație vectorială a principiului posibilelor deplasări.

Care este condiția necesară și suficientă pentru echilibrul unui sistem mecanic cu constrângeri geometrice staționare ideale?

Ce proprietate are funcția de rezistență a unui sistem conservator într-o stare de echilibru?

Scrieți un sistem de ecuații diferențiale Lagrange de al doilea fel.

Câte ecuații Lagrange de al doilea fel pot fi făcute pentru un sistem mecanic neliber?

Numărul de ecuații Lagrange ale unui sistem mecanic depinde de numărul de corpuri care alcătuiesc sistemul?

Ce se numește potențialul cinetic al unui sistem?

Pentru ce sisteme mecanice este disponibilă funcția Lagrange?

Ceea ce funcția argumentelor este vectorul viteză al unui punct aparținând unui sistem mecanic cu s grade de libertate?

Care este derivata parțială a vectorului viteză al unui punct din sistem în raport cu o viteză generalizată?

Funcția a căror argumente este energia cinetică a unui sistem supus unor constrângeri holonomice nestaționare?

Ce formă au ecuațiile Lagrange de al doilea fel? Care este numărul acestor ecuații pentru fiecare sistem mecanic?

Ce formă iau ecuațiile Lagrange de al doilea fel în cazul în care forțele conservatoare și neconservative acționează simultan asupra sistemului?

Ce este funcția Lagrange sau potențialul cinetic?

Ce formă au ecuațiile Lagrange de al doilea fel pentru un sistem conservator?

În funcție de ce variabile ar trebui exprimată energia cinetică a sistemului mecanic la elaborarea ecuațiilor Lagrange?

Cum se determină energia potențială a unui sistem mecanic sub influența forțelor elastice?

Sarcini pentru soluție independentă

Obiectivul 1. Aplicând principiul posibilelor deplasări, determinați reacțiile legăturilor structurilor compozite. Diagramele structurale sunt prezentate în fig. 15, iar datele necesare soluției sunt date în tabel. 1. În imagini, toate dimensiunile sunt în metri.

tabelul 1

R 1, kN R 2, kN q, kN/m M, kNm R 1, kN R 2, kN q, kN/m M, kNm

Opțiunea 1 Opțiunea 2

Opțiunea 3 Opțiunea 4

Opțiunea 5 Opțiunea 6

Opțiunea 7 Opțiunea 8

Fig. 16 Fig. 17

Soluţie. Este ușor de verificat că în această problemă sunt îndeplinite toate condițiile de aplicare a principiului Lagrange (sistemul este în echilibru, constrângerile sunt staționare, holonomice, limitative și ideale).

Renunțarea la legătura corespunzătoare reacției X A (fig. 17). Pentru a face acest lucru, în punctul A, balamaua fixă ​​ar trebui înlocuită, de exemplu, cu un suport de bară, iar sistemul primește un grad de libertate. După cum sa menționat deja, posibila mișcare a sistemului este determinată de constrângerile impuse acestuia și nu depinde de forțele aplicate. Prin urmare, determinarea posibilelor deplasări este o sarcină cinematică. Deoarece în acest exemplu cadrul se poate mișca doar în planul desenului, atunci posibilele sale mișcări sunt plate. În cazul mișcării plane, mișcarea corpului poate fi considerată ca o rotație în jurul centrului instantaneu de viteze. Dacă centrul instantaneu al vitezelor se află la infinit, atunci aceasta corespunde cu cazul mișcării instantanee de translație, când deplasările tuturor punctelor corpului sunt aceleași.

Pentru a găsi centrul instantaneu al vitezelor, este necesar să cunoaștem direcția vitezelor oricăror două puncte ale corpului. Prin urmare, determinarea posibilelor deplasări ale unei structuri compozite ar trebui să înceapă cu găsirea posibilelor deplasări ale elementului pentru care sunt cunoscute astfel de viteze. În acest caz, ar trebui să începeți cu cadrul. CDB din punctul său de vedere V este staționară și, prin urmare, posibila mișcare a acestui cadru este rotirea acestuia cu un unghi în jurul axei care trece prin balamaua B. Acum, cunoscând posibila mișcare a punctului CU(aparține simultan ambelor cadre ale sistemului) și posibilei mișcări a punctului A(o posibilă mișcare a punctului A este mișcarea acestuia de-a lungul axei X), găsim centrul instantaneu al vitezelor C 1 al cadrului AEC... Astfel, este posibilă mutarea cadrului AEC este rotația sa în jurul punctului C 1 cu un unghi. Relația dintre colțuri și este determinată prin mișcarea punctului C (vezi Fig. 17)

Din asemănarea triunghiurilor EC 1 C și BCD avem

Ca rezultat, obținem dependențele:

După principiul mișcărilor posibile

Să calculăm secvenţial posibilele locuri de muncă incluse aici:

Q = 2q este rezultanta sarcinii distribuite, al cărei punct de aplicare este prezentat în Fig. 79; posibila muncă pe care o face este egală.