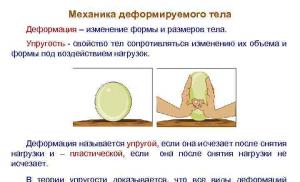
Metode neograničene optimizacije. Metode za bezuslovnu i uslovnu optimizaciju. Lista metoda neograničene optimizacije
od ukupnog skupa opcija, možete napraviti histogram, procijeniti koliko se često pronalaze dobre opcije i, na kraju, možete donijeti odluku - nastaviti pretragu ili se ograničiti na pronađeno rješenje.
Uprkos svestranosti i jednostavnosti postupka slučajnog sondiranja, on se ne može ograničiti zbog značajne računske složenosti. Dakle, metode ciljano pretraživanje rješenja.
4.5.3. Tehnike optimizacije bez ograničenja
Neophodni uslovi za postizanje ekstrema u svim gore navedenim oblicima dovode do rešenja sistema nelinearnih jednačina - veoma složenog i napornog problema (čak i u računarskoj matematici, rešenje nelinearnih jednačina se često svodi na određeni problem optimizacije) . Stoga se u praksi koriste drugi pristupi optimizaciji funkcija čije će razmatranje započeti takozvanim direktnim metodama. U nastavku ćemo govoriti o minimizaciji, dakle ekstrem je minimum.
Trenutno je razvijeno mnogo numeričkih metoda za bezuslovne i uslovne optimizacijske probleme. Kvalitet numeričke metode karakteriziraju mnogi faktori: brzina konvergencije, vrijeme izvršenja jedne iteracije, količina računarske memorije potrebne za implementaciju metode, klasa problema koje treba riješiti, itd. Problemi koje treba riješiti takođe su veoma raznoliki: mogu imati visoke i niske dimenzije, biti unimodalni i multiekstremalni itd. Isti metod, koji je efikasan za rešavanje problema jednog tipa, može se pokazati potpuno neprihvatljivim za probleme drugog tipa. .
Ispod je pregled glavnih metoda za rješavanje problema nelinearnog programiranja. Treba imati na umu da je čitava lista takvih metoda vrlo široka i ostaje otvorena. Osim toga, poznate su različite modifikacije za niz razmatranih metoda. Više informacija možete dobiti na
primjer, c.
Počnimo s razmatranjem direktnih metoda neograničene optimizacije kada nema ograničenja.
Smisao direktnih metoda neograničene optimizacije je da se konstruiše niz tačaka X, X, ..., X, kao što su
da je f (X)> f (X)>……> f (X). Za početnu tačku X može se izabrati proizvoljna tačka, međutim, oni teže da je izaberu što je moguće bliže minimalnoj tački. Prijelaz (iteracija) iz tačke X u tačku X, k = 0,1,2, ... sastoji se od dvije faze:
– izbor pravca kretanja od tačke NS ;
– određivanje koraka u ovom pravcu.
Metode za konstruiranje takvih nizova često se nazivaju metodama spuštanja, jer se vrši prijelaz s većih vrijednosti funkcije na manje.
Metode spuštanja su matematički opisane relacijom
X = X + a k p, k = 0,1,2, ...,
gdje je p jedinični vektor koji određuje smjer spuštanja;
a k - dužina koraka.
Različite metode spuštanja razlikuju se jedna od druge po načinu na koji biraju p i a k. U praksi se koriste samo metode sa konvergencijom. Oni dozvoljavaju konačan broj koraka da se dobije minimalna tačka ili joj se dovoljno približi. Kvalitet konvergirajućih iterativnih metoda se procjenjuje brzinom konvergencije.
Teoretski, metode spuštanja rješavaju problem u beskonačnom broju iteracija. U praksi, proračuni se prekidaju kada se ispune određeni kriterijumi (uslovi) za zaustavljanje iterativnog procesa. Na primjer, to može biti uvjet za malenost
argument |
X [k] - X [k - 1] |
||||||
f (X [k]) - f (X [k - 1])< γ . Здесь k – номер итерации; ε , γ – задан-
vrijednosti tačnosti rješenja problema.
Metode za pronalaženje minimalne tačke nazivaju se determinističkim ako su oba parametra prijelaza iz X u X (smjer kretanja i veličina koraka) jedinstveno odabrana iz informacija dostupnih u tački X. Ako se tokom tranzicije koristi bilo koji slučajni mehanizam, tada se algoritam pretraživanja naziva nasumično traženje minimuma.
Deterministički algoritmi za neograničenu minimizaciju podijeljeni su u klase ovisno o vrsti informacija koje se koriste. Ako se u svakoj iteraciji koriste samo vrijednosti minimiziranih funkcija, tada se metoda naziva metoda nultog reda. Ako je, pored toga, potrebno izračunavanje prvih izvoda funkcije koju treba minimizirati, tada postoje metode prvog reda,
ako je potrebno dodatno izračunati druge izvode - metode drugog reda.
Treba napomenuti da pri rješavanju problema neograničene minimizacije metode prvog i drugog reda imaju po pravilu veću stopu konvergencije od metoda nultog reda. Međutim, u praksi je izračunavanje prvog i drugog izvoda funkcije velikog broja varijabli vrlo naporno. U nekim slučajevima se ne mogu dobiti u obliku analitičkih funkcija. Derivati se određuju različitim numeričkim metodama s greškama koje mogu ograničiti primjenu takvih metoda. Osim toga, kriterijum optimalnosti se može specificirati ne eksplicitno, već putem sistema jednačina. U ovom slučaju postaje vrlo teško, a ponekad i nemoguće, analitički ili numerički pronaći derivate. Stoga su ovdje najdetaljnije metode nultog reda.
Metode jednodimenzionalnog pretraživanja. Lista metoda za jednodimenzionalno pretraživanje - numeričko traženje ekstremuma funkcije jednog argumenta f (x ) Dovoljno je širok i dobro pokriven u literaturi. Stoga ćemo se ovdje ograničiti na razmatranje samo jedne metode, koja je, prema iskustvu autora, jedna od najefikasnijih - metoda „zlatnog preseka“.
Ideja metode je da se sukcesivno smanji interval nesigurnosti - interval vrijednosti argumenta x koji sadrži traženu minimalnu tačku - na dužinu koja ne prelazi
dozvoljena greška rezultata ε. Kao početni interval, dozvoljeni raspon vrijednosti argumenta specificiran uvjetima problema ili, u slučaju kada potonji nema lijevu i (ili) desnu granicu, neko područje unutar dopuštenog, na koje se potrebni minimum je naznačen preliminarnom analizom, može se uzeti u obzir.
Svaki interval sadrži dvije tačke x = y 0 i x = z 0, koje ispunjavaju svoj "zlatni rez" - podjelu na dva nejednaka dijela tako da se omjer većeg dijela i dužine cijelog intervala poklapa sa omjerom manji dio prema većem. Očigledno, ove tačke se nalaze simetrično oko centra intervala (slika 26). Koordinate tačaka "zlatnog preseka" mogu se pronaći iz odgovarajućih proporcija:
b - y0 |
y0 - a |
= δ , |
z0 - a |
b - z0 |
= δ, |
||||
b - a |
b - y |
b - a |
- a |
||||||

odakle je lako dobiti δ = (1 – δ) / δ i doći do jednačine: δ 2 + δ –1 = 0. Kao rezultat dobijamo relativne udjele koji određuju „zlatni presjek“ intervala: δ = 0,618, 1 – δ = 0,382. “Zlatni presek” ima važno svojstvo: tačka y 0 je jedna od tačaka “zlatnog preseka” intervala, tačka z 0 je jedna od tačaka “zlatnog preseka” intervala. Ovo će osigurati
čeka se jednostavna računica: 0,382 / 0,618 = 0,618 i (0,618–0,382) / 0,618 = = 0,382.
Algoritam za pronalaženje minimuma, izgrađen na osnovu metode „zlatnog preseka“, predviđa pri svakoj iteraciji izbor kao jedne od granica redukovanog intervala leve ili desne tačke „zlatnog preseka“ tako da se potrebni minimum ostaje unutar njega:
1. Postavite k = 0, početni interval nesigurnosti, dozvoljenu grešku rezultata ε.
2. Izračunajte koordinate tačaka "zlatnog preseka":
y k = a k +0,382 (b k –a k), z k = a k +0,618 (b k –a k).
3. Izračunajte vrijednosti funkcije cilja u pronađenim tačkama
f (y k) i f (z k).
4. Ako je f (yk) ≤f (zk) (slika 26, a), dodijeliti ak + 1 = ak, bk + 1 = zk, zk + 1 = yk, yk + 1 = ak + zk –yk, k = k +1. Inače (slika 26, b) a k + 1 = y k, b k + 1 = b k, y k + 1 = z k, z k + 1 = y k + b k –z k, k = k +1.
5. Provjerite ispunjenost uvjeta završetka pretraživanja
b k + 1 - a k + 1 ≤ ε. Ako je ispunjeno, kao rješenje se bira tačka x = (y k + 1 + z k + 1) 2. U suprotnom, idite na korak 2.
Računska efikasnost metode "zlatnog preseka" je zbog činjenice da je ovde, pri svakoj iteraciji, potrebno samo jedno izračunavanje vrednosti funkcije cilja.
Metoda direktne pretrage (Hook-Jeeves metoda). Neki
druga početna tačka X. Naizmjeničnim mijenjanjem komponenti vektora X ispituje se susjedstvo ove tačke, uslijed čega se nalazi tačka (nova baza) koja određuje smjer u kojem se smanjuje minimizirana funkcija f (X). Spuštanje se vrši u odabranom smjeru, pazeći da se vrijednost funkcije smanji. Procedura se ciklički ponavlja sve dok nije moguće pronaći smjer spuštanja, uzimajući u obzir prihvaćeni uvjet zaustavljanja.
Algoritam metode direktnog pretraživanja u svom najopćenitijem obliku može se formulirati na sljedeći način:
1. Postavljeno vrijednostima koordinata x i, i = 1,2, ... n, početne tačke (k = 0), vektora početnih prirasta koordinata
∆ X = (∆ x 1, ∆ x 2, ..., ∆ xn) tokom snimanja okoline, najmanja dozvoljena vrijednost ε komponenti ∆ X, faktor ubrzanja λ ≥ 1, koji određuje brzinu spuštanja, faktor skale d> 1.
2. Uzmite X za "staru osnovu": X b = X. Izračunati
vrijednost f (X b).
3. Naizmjenično mijenjajte svaku koordinatu x b i, i = 1,2, ... n,
tačke X b po vrijednosti ∆ x i, odnosno uzmimo x i = x b i + ∆ x i, tada
x i = x b i –∆ x i. Izračunajte vrijednosti f (X) na dobijenim tačkama uzorka i uporedite ih sa vrijednosti f (X b). Ako je f (X)< < f
(X
б
), то соответствующая координата х
i
приобретает новое значение, вычисленное по одному из приведенных выражений. В противном случае значение этой координаты остается неизменным. Если после изменения последней n
-й координаты f
(X
) 4. Izvršiti spuštanje u pravcu od "stare" do "nove" baze kroz posljednju, odnosno izračunati koordinate nove tačke X: x i = x i + λ (x i –x bi), i = 1,2,… n. Izračunajte f (X) vrijednost. Ako je uslov f (X) "Nova" osnova se uzima kao "stara" (X b = X, f (X b) = f (X)) i ide se na korak 5. U suprotnom, uzmite xi = xi, i = 1,2, ... n ... 5.
Kao na str.3, naizmjenično mijenjajte svaku koordinatu tačke X, upoređujući odgovarajuće vrijednosti funkcije f (X) sa vrijednošću f (X) dobijenom u koraku 4. Nakon promjene posljednje koordinate, uporedite odgovarajuću vrijednost funkcija f (X) sa vrijednošću f (X b) dobijenom u odjeljku 4. Ako je f (X) 6. Ako za sve i ∆ x i<ε
, вычисления прекращаются. В противном случае уменьшают значения ∆
х
i
в d
раз и переходят к п. 3. Rad algoritma je ilustrovan na Sl. 27. Prikaz linija nivo minimizirane funkcije f (x 1, x 2), odnosno linije dobijene iz uslova f (x 1, x 2) = f 1 = const, f (x 1, x 2) = f 2 = const, i tako dalje. Ovdje je f 1> f 2> f 3. Pune linije su rezultat jednog izvršavanja koraka. 3 ... 5 (traženje smjera opadanja funkcije i spuštanje), isprekidana linija - sljedeći spust. Prednost metode direktnog pretraživanja je jednostavnost programiranja na računaru. Ne zahtijeva eksplicitno poznavanje funkcije cilja, a također lako uzima u obzir ograničenja na pojedinačne varijable, kao i složena ograničenja na opseg pretraživanja. Nedostatak metode direktne pretrage je u tome što u slučaju jako izduženih, zakrivljenih ili oštrih linija na nivou funkcije cilja, možda neće moći osigurati napredak do minimalne tačke zbog ograničenog broja analiziranih pravaca. Metoda deformabilnog poliedra (Nelder-Mead metoda) je to za minimiziranje funkcije n varijabli f (X) u n-dimenzionalnoj prostoru, konstruiše se poliedar koji sadrži n +1 vrh. Očigledno, svaki vrh odgovara nekom vektoru Xi ... Izračunajte vrijednosti ciljne funkcije f (Xi), i = 1,2, ..., n +1, na svakom od vrhova poliedra, odredite maksimum ovih vrijednosti i odgovarajući vrh Xh ... Kroz ovaj vrh i težište preostalih vrhova povlači se projekcijska linija na kojoj se nalazi tačka Xq sa manjom vrijednošću funkcije cilja nego na vrhu Xh (Sl. 28, a ). Zatim isključite vrh Xh ... Od preostalih vrhova i tačaka Xq konstruiše se novi poliedar sa kojim se ponavlja opisani postupak. U procesu izvođenja ovakvih operacija, poliedar mijenja svoju veličinu, zbog čega je metoda i dobila ime. Uvedemo sljedeću notaciju: X je vektor koordinata i-tog vrha poliedra u k-tom koraku traženja, i = 1,2,… n +1, k = 1,2,…; h - broj vrha u kojem je vrijednost cilja gume, osim X. Koordinate centra gravitacije proračuna xj [n + 2, k] = n + 1 izračunavaju se prema formuli ∑ xj [i, k] - xj [h, k] J = 1,2, ... n. j = 1 Približan algoritam za metodu deformabilnog poliedra je sljedeći: 1.
Postavljen koeficijentima refleksijeα, napetost γ> 1, kompresija β<1
, допустимой погрешностью определения координат tačke minimuma ε. Odabiru se koordinate vrhova originalnog poliedra X, i = 1,2, ... n +1, k = 1. 2.
Izračunajte vrijednosti ciljne funkcije na svim vrhovima f (X), i = 1,2, ... n +1, i pronađite tačke X, X (na slici 28, b, tačke X 2 i X 1, respektivno), kao i X. 3.
Izvršiti projekciju tačke X kroz centar list: X = X + α (X –X). 4. Ako je f (X) ≤ X, izvršite operaciju istezanja. niya: X = X + γ (X –X). U suprotnom idite na stavku 6. 5.
Konstruiše se novi poliedar: ako f (X) zamjenom X sa X, u suprotnom, zamjenom X sa X. Proračuni se nastavljaju od tačke 2 za k = k +1. 6. Ako X> f (X)> X za sve i nije jednako h, izvrši operaciju kompresije: X = X + β (X - X). Novi politop se konstruiše zamjenom X sa X i proračuni se nastavljaju od tačke 2 za k = k +1. 7. Ako je f (X)> X, onda, zadržavajući vrh X, konstruisati novi poliedar sličan trenutnom prepolovljavanjem dužina svih ivica: X = X +0,5 (X –X) i nastaviti proračune iz stavka 2 za k = k +1. U str. 6, 7, prije nego što se pređe na tačku 2, potrebno je provjeriti da li je ispunjen uslov za završetak traženja minimuma, npr. prema uslovu pogled max n ∑ + 1 (x j [i, k] - x j [n + 2, k]) 2< ε
2
. i j = 1 WITH Koristeći operaciju rastezanja i kompresije, dimenzije i oblik deformabilnog poliedra se prilagođavaju topografiji ciljne funkcije. Kao rezultat toga, poliedar se proteže duž dugih nagnutih površina, mijenja smjer u zakrivljenim udubljenjima i skuplja se u blizini minimuma, što određuje učinkovitost razmatrane metode. α = 1, 2≤ γ ≤3, 0,4≤β ≤0,6. Metoda rotirajućih koordinata (Rosenbrockova metoda). Njegova suština se sastoji u uzastopnim rotacijama koordinatnog sistema u skladu sa promjenom smjera najbržeg opadanja funkcije cilja (slika 29). Od početne tačke X spusti se do tačke X u pravcima paralelnim sa koordinatnim osama. U sljedećoj iteraciji, jedna od osi mora proći u smjeru x'1 = X - X, ostalo - u pravcima okomitim na x'1 ... Spuštanje duž ovih osovina vodi do točke X , što omogućava konstruisanje novog vektora x''1 = X - X a na osnovu njega novi sistem pravaca pretraživanja minimum bodova X. V Za razliku od drugih metoda nultog reda, Rosenbrockova metoda se fokusira na pronalaženje optimalne tačke u svakom smjeru, a ne samo na fiksni pomak u svim smjerovima. Veličina koraka u procesu pretraživanja kontinuirano se mijenja ovisno o topografiji nivelisane površine. Kombinacija rotacije koordinata sa kontrolom koraka čini Rosenbrockovu metodu efikasnom u rješavanju složenih problema optimizacije. V Konkretno, ova metoda je, za razliku od mnogih drugih, efikasna u minimiziranju takozvanih funkcija "jaruga" (sa jako izduženim ravnim površinama), budući da rezultirajući smjer pretraživanja teži da se nalazi duž ose "jaruga". Metoda paralelne tangente (Powellova metoda). Njegova se suština sastoji u sekvencijalnom sprovođenju jednodimenzionalne potrage za minimumom funkcije cilja u odnosu na n + 1 smjer od poznatih jednodimenzionalnih metoda. Na prvoj iteraciji, kao prva n pravci se biraju koordinata, kao(n + 1) th smjerovima koristi se prvi od njih (sl. 30). U svakoj narednoj iteraciji, pretraga počinje iz drugog smjera prethodne iteracije, odnosno brojevi smjerova se smanjuju za jedan;(n + 1) th smjer sljedeće iteracije je dat vektorom X– X [n + 1] - od minimalne tačke pronađene u prvom koraku prethodne iteracije preko minimalne tačke pronađene u njenom poslednjem koraku. Među metodama optimizacije nultog reda u CAD-u koriste se Rozenbrokove metode, konfiguracije, deformabilni poliedar i slučajna pretraga. Metode koje koriste derivate uključuju metode najstrmijeg spuštanja, konjugirane gradijente, varijabilne metrike. Rosenbrockova metoda je poboljšana verzija koordinatnog spuštanja. Metoda koordinatnog spuštanja karakteriziran izborom pravaca traženja naizmjenično duž svih koordinatnih osa, korak se izračunava na osnovu jednodimenzionalne optimizacije, kriterij završetka pretraživanja, gdje je specificirana tačnost određivanja lokalnog ekstremuma, je dimenzija prostora kontrolisanih parametara. Koordinatna putanja spuštanja za primjer dvodimenzionalnog prostora kontroliranih parametara prikazana je na Sl. 1, gdje su tačke na putanji traženja, su kontrolirani parametri. Funkcija cilja je predstavljena vlastitim linijama jednakog nivoa; odgovarajuća vrijednost je upisana u blizini svake linije. Očigledno, postoji minimalna tačka. Rice. 1. Trajektorija koordinatnog spuštanja Kada se koristi metoda koordinatnog spuštanja, postoji velika vjerovatnoća da se pretraga "zaglavi" na dnu jaruge, daleko od tačke ekstrema. Na sl. 2 vidi se da nakon udarca u tačku koja se nalazi na dnu jaruge dalji koraci su mogući samo u smjerovima ili, ali dovode do pogoršanja funkcije cilja. Stoga se pretraga zaustavlja na jednoj tački. Napomena 1 Jaruga je dio prostora kontrolisanih parametara u kojem se uočavaju slabe promjene derivacija funkcije cilja u jednom smjeru i značajne promjene sa promjenom predznaka u nekim drugim smjerovima. Predznak derivacije se mijenja na tačkama koje pripadaju dnu jaruge. Rice. 3. Putanja koordinatnog spuštanja uz povoljnu orijentaciju koordinatnih osa Rosenbrockova metoda sastoji se u takvoj rotaciji koordinatnih osa tako da jedna od njih ispada kvaziparalelna s dnom jaruge. Ovo skretanje se izvodi na osnovu podataka dobijenih nakon niza koordinatnih koraka spuštanja. Položaj novih osa može se dobiti linearnom transformacijom starih osa: os se poklapa u pravcu sa vektorom; preostale ose se biraju iz uslova ortogonalnosti na i jedna na drugu. Još jedna uspješna modifikacija koordinatnog spuštanja je metoda konfiguracije(Hook-Jeeves). U skladu sa ovom metodom, prvo se izvodi uobičajena serija koordinatnih koraka spuštanja, a zatim se pravi dodatni korak u pravcu vektora, kao što je prikazano na sl. 4, gdje se izvodi dodatni korak u smjeru vektora koji vodi do tačke. Rice. 4. Ilustracija metode konfiguracije Pronalaženje ekstremuma metoda deformabilnog poliedra(Nelder-Mead) zasniva se na konstrukciji poliedra sa vrhovima u svakom koraku pretraživanja, gdje je dimenzija prostora kontroliranih parametara. Na početku pretrage, ovi vrhovi se biraju proizvoljno; u narednim koracima izbor je podložan pravilima metode. Ova pravila su objašnjena na sl. 5 na primjeru dvodimenzionalnog problema optimizacije. Vrhovi originalnog trokuta su odabrani:,,. Novi vrh se nalazi na zraku povučenom od najgoreg vrha (od temena sa najvećom vrijednošću funkcije cilja) kroz težište poliedra, a preporučuje se odabir na udaljenosti od jednake do. Novi gornji dio zamjenjuje najgori gornji dio. Ako se pokaže da ima najbolju vrijednost ciljne funkcije među vrhovima poliedra, tada se udaljenost povećava. Na slici se dešava ova situacija i povećanje daje poen. U novom poliedru sa vrhovima,, najgori je vrh, shodno tome se dobija vrh, zatim vrh, itd. Ako se novi vrh pokaže kao najgori, onda najbolji vrh treba zadržati u poliedru, a dužine svih ivica treba smanjiti, na primjer, za polovicu (kontrakcija poliedra na najbolji vrh). Pretraživanje se zaustavlja kada se ispuni uslov za smanjenje veličine poliedra na određenu granicu. korak je izabran kao optimalan korišćenjem jednodimenzionalne optimizacije. Kada se koristi metoda najstrmijeg spuštanja, kao i većina drugih metoda, efikasnost pretraživanja je značajno smanjena u situacijama u jaruzi. Traktorija pretraživanja poprima cik-cak oblik sa polaganim napredovanjem po dnu jaruge prema krajnosti. Nekoliko tehnika se koristi za poboljšanje efikasnosti gradijentnih metoda. Jedna od tehnika koje se koriste u metoda konjugiranog gradijenta(takođe nazvana Fletcher-Reeves metoda), zasniva se na konceptu vektorske konjugacije. Vektori i nazivaju se -konjugirani ako je, gdje je pozitivno određena kvadratna matrica istog reda kao i veličina vektora i (poseban slučaj konjugacije je ortogonalnost vektora kada je to matrica jediničnog reda), vektor reda , je vektor stupca. Posebnost konjugiranih pravaca za, gdje je Hessian matrica, u problemima s kvadratnom ciljnom funkcijom je sljedeća: jednodimenzionalna minimizacija sekvencijalno duž konjugiranih pravaca omogućava pronalaženje ekstremne tačke u ne više od koraka. Napomena 2 Hessian matrica je matrica drugih parcijalnih izvoda ciljne funkcije u odnosu na kontrolirane parametre. Razlog za korišćenje pretrage u -susednim pravcima je taj što se za funkcije () opšteg oblika može primeniti kvadratna aproksimacija, što u praksi rezultira izvođenjem pretrage u više od koraka. Potraga za ekstremom se vrši u skladu sa formulom Pošto se korak računa na osnovu uslova jednodimenzionalne optimizacije, tada je, prvo, relacija Algoritam pretrage se svodi na primenu formule (3) sve dok se ne ispuni uslov za kraj proračuna Za određivanje koeficijenta, sistem jednačina (2) - (7) se rješava zamjenom u (4) vrijednosti iz (3) i iz (2): Ako proces konvergira, tada se rješenje postiže u malom broju iteracija, čiji je kraj ispunjenje uvjeta Zbog toga Može se pokazati da teži, - do at, gdje je dimenzija prostora kontroliranih parametara. Nakon koraka, morate ponovo početi sa. Klasične metode neograničene optimizacije Uvod Kao što znate, klasični problem neograničene optimizacije ima oblik: Za rješavanje ovih problema postoje analitičke i numeričke metode. Prije svega, podsjetimo se analitičkih metoda za rješavanje problema neograničene optimizacije. Metode neograničene optimizacije zauzimaju značajno mjesto u kursu ML. To je zbog njihove direktne primjene u rješavanju niza optimizacijskih problema, kao i u implementaciji metoda za rješavanje značajnog dijela uvjetnih optimizacijskih problema (MT problema). 1. Neophodni uslovi za tačku lokalnog minimuma (maksimuma) Neka m isporučuje minimalne vrijednosti funkcije. Poznato je da je u ovom trenutku prirast funkcije nenegativan, tj. Pronađimo, koristeći proširenje funkcije u blizini m u Taylorov red. gdje je zbir članova niza čiji je redoslijed relativan u odnosu na priraštaje (dva) i više. Iz (4) jasno proizlazi da Pretpostavimo onda Uzimajući u obzir (6) imamo:. (7) Pretpostavimo da je pozitivan, tj. ... Odaberimo, dakle, proizvod koji je u suprotnosti (1). Stoga je to zaista očigledno. Slično argumentirajući u odnosu na druge varijable, dobijamo neophodan uslov za tačke lokalnog minimuma funkcije nekoliko varijabli Lako je dokazati da će neophodni uslovi za tačku lokalnog maksimuma biti potpuno isti kao i za tačku lokalnog minimuma, tj. uslovi (8). Jasno je da će rezultat dokaza biti nejednakost oblika: - uvjet za nepozitivan prirast funkcije u susjedstvu lokalnog maksimuma. Dobijeni neophodni uslovi ne daju odgovor na pitanje: da li je stacionarna tačka minimalna ili maksimalna tačka. Odgovor na ovo pitanje može se dobiti ispitivanjem dovoljnih uslova. Ovi uvjeti podrazumijevaju proučavanje matrice drugih izvoda ciljne funkcije. 2. Dovoljni uslovi za tačku lokalnog minimuma (maksimuma) Predstavljamo proširenje funkcije u susjedstvu tačke u Taylorovom redu do kvadratnog u terminima. Ekspanzija (1) se može sažetije predstaviti korištenjem koncepta: "tačkasti proizvod vektora" i "vektorsko-matrični proizvod". Matrica dva izvoda ciljne funkcije u odnosu na odgovarajuće varijable. Povećanje funkcije zasnovano na (1") može se napisati kao: S obzirom na neophodne uslove: Zamjena (3) u obliku: Kvadratni oblik se naziva diferencijalni kvadratni oblik (DKF). Ako je DKF pozitivno određen, tada je stacionarna tačka također lokalna minimalna tačka. Ako su DKF i matrica koja ga predstavlja negativno definirani, tada je stacionarna tačka također lokalna tačka maksimuma. Dakle, potrebni i dovoljni uslovi za tačku lokalnog minimuma imaju oblik (isti neophodni uslovi se mogu napisati na sledeći način: Dovoljno stanje. Prema tome, nužan i dovoljan uslov za lokalni maksimum ima oblik: Prisjetimo se kriterija za određivanje da li su kvadratni oblik i matrica koja ga predstavlja pozitivno ili negativno definitivna. 3. Silvesterov kriterijum Omogućava vam da odgovorite na pitanje: da li je kvadratni oblik i matrica koja ga predstavlja pozitivno određeni ili negativno određeni. Zove se Hesseova matrica. Glavna determinanta Hesseove matrice a DKF koji predstavlja bit će pozitivno definitivan ako su sve glavne determinante Hesove matrice () pozitivne (tj., odvija se sljedeća shema predznaka: Ako postoji drugačija shema predznaka za glavne determinante Hessian matrice, na primjer, tada su matrica i DKF negativno definirani. 4. Ojlerova metoda je klasična metoda za rješavanje neograničenih optimizacijskih problema Ova metoda se zasniva na neophodnim i dovoljnim uslovima proučavanim u 1.1 do 1.3; primjenjujemo samo na pronalaženje lokalnih ekstrema kontinuiranih diferencijabilnih funkcija. Algoritam za ovu metodu je prilično jednostavan: 1) koristeći potrebne uslove, formiramo sistem nelinearnih jednačina u opštem slučaju. Imajte na umu da je generalno nemoguće analitički riješiti ovaj sistem; potrebno je primijeniti numeričke metode za rješavanje sistema nelinearnih jednačina (NE) (vidi "FM"). Iz tog razloga, Eulerova metoda će biti analitičko-numerička metoda. Rješavajući navedeni sistem jednačina, nalazimo koordinate stacionarne tačke .; 2) istražujemo DKF i Hesovu matricu koja ga predstavlja. Koristeći Sylvesterov kriterij, utvrđujemo da li je stacionarna tačka minimalna ili maksimalna tačka; 3) izračunati vrijednost ciljne funkcije u ekstremnoj tački Koristeći Eulerovu metodu, riješite sljedeći problem neograničene optimizacije: pronađite 4 stacionarne točke funkcije oblika: Saznajte prirodu ovih tačaka, bilo da su to minimalne tačke ili sedla (vidi). Konstruisati grafički prikaz ove funkcije u prostoru i na ravni (pomoću linija nivoa). 5. Klasični problem uslovne optimizacije i metode za njegovo rješavanje: Metoda eliminacije i Metoda Lagrangeovih množitelja (MLM) Kao što znate, klasični problem uslovne optimizacije ima oblik: Grafikon koji objašnjava iskaz problema (1), (2) u prostoru. Jednačine linije nivoa Dakle, ODR u problemu koji se razmatra je određena kriva predstavljena jednadžbom (2"). Kao što vidite na slici, tačka je tačka bezuslovnog globalnog maksimuma; tačka - tačka uslovnog (relativnog) lokalnog minimuma; tačka - tačka uslovnog (relativnog) lokalnog maksimuma. Zadatak (1"), (2") se može riješiti metodom eliminacije (supstitucije), rješavanjem jednadžbe (2") u odnosu na varijablu i zamjenom pronađenog rješenja (1"). Izvorni problem (1"), (2") se tako transformira u problem neograničene optimizacije funkcije, koji se lako može riješiti Ojlerovom metodom. Metoda isključenja (supstitucije). Neka funkcija cilja zavisi od varijabli: nazivaju se zavisne varijable (ili varijable stanja); shodno tome, možemo uvesti vektor Preostale varijable se nazivaju nezavisne varijable odluke. U skladu s tim, možemo govoriti o vektoru stupca: i vektori. U klasičnom problemu uslovne optimizacije: Sistem (2), u skladu sa metodom isključenja (supstitucije), mora biti razriješen u odnosu na zavisne varijable (varijable stanja), tj. treba dobiti sljedeće izraze za zavisne varijable: Da li je sistem jednadžbi (2) uvijek rješiv u odnosu na zavisne varijable - ne uvijek, to je moguće samo u slučaju kada je determinanta, nazvana Jakobijan, čiji elementi imaju oblik: nije jednako nuli (pogledajte odgovarajuću teoremu u MA kursu) Kao što vidite, funkcije moraju biti kontinuirane diferencijabilne funkcije, a drugo, elementi determinante moraju biti izračunati u stacionarnoj tački ciljne funkcije. Zamjenom iz (3) u ciljnu funkciju (1), imamo: Istražena funkcija za ekstrem se može proizvesti Ojlerovom metodom - metodom neograničene optimizacije kontinuirano diferencibilne funkcije. Dakle, metoda eliminacije (supstitucije) omogućava korištenje problema klasične uslovne optimizacije da se transformiše u problem bezuslovne optimizacije funkcije - funkcije varijabli pod uslovom (4), što omogućava dobijanje sistema izraza ( 3). Nedostatak metode eliminacije: poteškoće, a ponekad i nemogućnost dobijanja sistema izraza (3). Bez ovog nedostatka, ali koji zahteva ispunjenje uslova (4), je MLM. 5.2. Lagrangeova metoda množenja. Neophodni uslovi u klasičnom problemu uslovne optimizacije. Lagrangeova funkcija MLM dozvoljava originalni problem klasične uslovne optimizacije: Transformirajte posebno dizajniranu funkciju - Lagrangeovu funkciju u problem neograničene optimizacije: gdje, - Lagrangeovi množitelji; Kao što vidite, to je zbir koji se sastoji od originalne funkcije cilja i "ponderisanog" zbira funkcija - funkcija koje predstavljaju njihova ograničenja (2) originalnog problema. Neka je tačka tačka bezuslovnog ekstremuma funkcije, tada, kao što je poznato, ili (ukupni diferencijal funkcije u tački). Korištenje koncepta zavisnih i nezavisnih varijabli - zavisnih varijabli; su nezavisne varijable, onda predstavljamo (5) u proširenom obliku: Iz (2) je očigledno da sistem jednadžbi oblika slijedi: Rezultat izračunavanja ukupnog diferencijala za svaku od funkcija Predstavljamo (6) u "proširenom" obliku, koristeći koncept zavisnih i nezavisnih varijabli: Imajte na umu da je (6"), za razliku od (5"), sistem koji se sastoji od jednačina. Pomnožimo svaku -tu jednačinu sistema (6") odgovarajućim --tim Lagrangeovim množiteljem. Saberimo ih i sa jednačinom (5") i dobijemo izraz: Uredimo Lagrangeove množitelje na način da je izraz u uglastim zagradama pod predznakom prve sume (drugim riječima, koeficijenti na diferencijalima nezavisnih varijabli,) jednak nuli. Izraz "odbaciti" Lagrangeove množitelje na gore navedeni način znači da je potrebno riješiti određeni sistem jednačina u odnosu na. Struktura takvog sistema jednadžbi može se lako dobiti izjednačavanjem izraza u uglastim zagradama pod znakom prvog zbira sa nulom: Prepisujemo (8) kao Sistem (8") je sistem linearnih jednadžbi u odnosu na poznate: Sistem je rješiv ako (zbog toga, kao u metodi eliminacije u predmetnom slučaju, mora biti zadovoljen uslov). (9 ) Pošto je u ključnom izrazu (7) prvi zbir jednak nuli, lako je shvatiti da će i drugi zbir biti jednak nuli, tj. vrijedi sljedeći sistem jednačina: Sistem jednačina (8) se sastoji od jednačina, a sistem jednačina (10) se sastoji od jednačina; svih jednačina u dva sistema i nepoznanica Jednačine koje nedostaju date su sistemom jednačina ograničenja (2): Dakle, postoji sistem jednadžbi za pronalaženje nepoznanica: Dobiveni rezultat je da sistem jednačina (11) čini glavni sadržaj MLM-a. Lako je shvatiti da se sistem jednačina (11) može dobiti vrlo jednostavno uvođenjem u razmatranje posebno konstruisane Lagrangeove funkcije (3). Zaista Dakle, sistem jednačina (11) se može predstaviti u obliku (pomoću (12), (13)): Sistem jednačina (14) predstavlja neophodan uslov u klasičnom problemu uslovne optimizacije. Rezultirajuće rješenje ovog sistema, vrijednost vektora naziva se uslovno stacionarna tačka. Da bi se saznala priroda uslovno stacionarne tačke, potrebno je koristiti dovoljne uslove. 5.3 Dovoljni uslovi u klasičnom problemu uslovne optimizacije. MML algoritam Ovi uvjeti omogućavaju da se utvrdi da li je uvjetno stacionarna tačka tačka lokalnog uslovnog minimuma ili tačka lokalnog uslovnog maksimuma. Relativno jednostavno, kao što su u zadatku dobijeni dovoljni uslovi za bezuslovni ekstrem. Dovoljni uslovi se takođe mogu dobiti u klasičnom problemu uslovne optimizacije. Rezultat ove studije: gdje je tačka lokalnog uslovnog minimuma. gdje je tačka lokalnog uslovnog maksimuma, je Hessian matrica sa elementima Hesseova matrica ima dimenzije. Dimenzija Hesseove matrice može se smanjiti korištenjem uvjeta nejednakosti na nulu Jakobijana:. Pod ovim uslovom, zavisne varijable se mogu izraziti kao nezavisne varijable, tada će Hessian matrica imati dimenzije, tj. potrebno je govoriti o matrici sa elementima tada će dovoljni uslovi biti sljedeći: Tačka lokalnog uvjetnog minimuma. Tačka lokalnog uvjetnog maksimuma. Dokaz: MML algoritam: 1) sastaviti Lagrangeovu funkciju:; 2) koristeći potrebne uslove, formiramo sistem jednačina: 3) naći tačku iz rješenja ovog sistema; 4) koristeći dovoljne uslove, odredimo da li je tačka tačka lokalnog uslovnog minimuma ili maksimuma, zatim nalazimo 1.5.4. Grafoanalitička metoda za rješavanje klasičnog problema uvjetne optimizacije u prostoru i njegove modifikacije pri rješavanju najjednostavnijih problema IP i AP Ova metoda koristi geometrijsku interpretaciju klasičnog problema ograničene optimizacije i zasniva se na brojnim važnim činjenicama svojstvenim ovom problemu. B je zajednička tangenta za funkciju i funkciju koja predstavlja ODR. Kao što vidite na slici, tačka je tačka bezuslovnog minimuma, tačka je tačka uslovnog lokalnog minimuma, tačka je tačka uslovnog lokalnog maksimuma. Dokažimo da je u tačkama uslovnih lokalnih ekstrema kriva i odgovarajuće linije nivoa Iz magistarskog kursa je poznato da je u tački tangente uslov gdje je nagib tangente povučen odgovarajućom linijom nivoa; je nagib tangente na funkciju Izraz (MA) za ove koeficijente je poznat: Dokažimo da su ovi koeficijenti jednaki. jer o tome "govore" potrebni uslovi Gore navedeno nam omogućava da formuliramo HFA algoritam za metodu za rješavanje klasičnog problema ograničene optimizacije: 1) gradimo porodicu linija nivoa funkcije cilja: 2) konstruiramo ODR koristeći jednadžbu ograničenja 3) da bismo ispravili porast funkcije, pronalazimo i razjašnjavamo prirodu ekstremnih tačaka; 4) istražujemo interakciju linija nivoa i funkcije, dok iz sistema jednačina nalazimo koordinate uslovno stacionarnih tačaka – lokalnih uslovnih minimuma i lokalnih uslovnih maksimuma. 5) izračunati Posebno treba napomenuti da se glavne faze HFA metode za rješavanje klasičnog problema ograničene optimizacije poklapaju sa glavnim fazama HFA metode za rješavanje NP i LP problema, jedina razlika je u ODR-u, kao i u pronalaženju lokacija ekstremnih tačaka u ODR-u (na primjer, u LP problemima, ove tačke se nužno nalaze na vrhovima konveksnog poligona koji predstavlja ODR). 5.5. O praktičnom značenju MML-a Hajde da predstavimo klasični problem uslovne optimizacije u obliku: gdje su varijabilne veličine koje predstavljaju promjenjive resurse u primijenjenim tehničkim i ekonomskim problemima. U prostoru, problem (1), (2) ima oblik: gdje je varijabla. (2") Neka je tačka uslovnog ekstremuma: Kada se promijeni, mijenja se Vrijednost ciljne funkcije će se promijeniti u skladu s tim: Izračunajmo derivaciju: Iz (3), (4), (5). (6) Zamijenite (5") u (3) i dobijete: Iz (6) da Lagrangeov množitelj karakterizira vrijednost "reakcije" (ortogonalnu vrijednosti ciljne funkcije) na promjene parametra. Općenito, (6) ima oblik: Iz (6), (7), faktor karakterizira promjenu kada se odgovarajući --ti resurs promijeni za 1. Ako je maksimalni profit ili minimalni trošak, onda karakterizira promjene ove vrijednosti pri promjeni, za 1. 5.6. Klasični problem ograničene optimizacije kao problem nalaženja sedla Lagrangeove funkcije: Par se naziva sedlo ako vrijedi nejednakost. Očigledno, iz (1). (2) Iz (2) to. (3) Kao što vidite, sistem (3) sadrži jednačine slične onim jednačinama koje predstavljaju neophodan uslov u klasičnom problemu uslovne optimizacije: gdje je Lagrangeova funkcija. U vezi sa analogijom sistema jednačina (3) i (4), klasični problem uslovne optimizacije može se posmatrati kao problem nalaženja sedla Lagrangeove funkcije. Problemi višedimenzionalne optimizacije u proučavanju tehnoloških procesa u tekstilnoj industriji, analiza nastalih poteškoća. Pronalaženje ekstrema, kao što je ekstrem, vrijednost ciljne funkcije neograničene višedimenzionalne optimizacije. test, dodano 26.11.2011 Karakterizacija klasičnih metoda neograničene optimizacije. Određivanje neophodnog i dovoljnog uslova za postojanje ekstremuma funkcija jedne i više varijabli. Lagrangeovo pravilo množitelja. Potrebni i dovoljni uslovi za optimalnost. seminarski rad dodan 13.10.2013 Metode i karakteristike rješavanja problema optimizacije, posebno na raspodjeli investicija i izboru putanje u transportnoj mreži. Specifičnosti modeliranja primjenom Hamming i Brown metoda. Identifikacija, stimulacija i motivacija kao funkcije upravljanja. test, dodano 12.12.2009 Iskaz, analiza, grafičko rješenje problema linearne optimizacije, simpleks metoda, dualnost u linearnoj optimizaciji. Formulacija transportnog problema, svojstva i pronalaženje referentnog rješenja. Uslovna optimizacija pod ograničenjima jednakosti. priručnik, dodano 07.11.2010 Kritična putanja u grafu. Optimalna distribucija protoka u transportnoj mreži. Problem linearnog programiranja riješen grafički. Neuravnotežen transportni izazov. Numeričke metode za rješavanje jednodimenzionalnih problema statičke optimizacije. seminarski rad dodan 21.06.2014 Grafička metoda za rješavanje problema optimizacije proizvodnih procesa. Primjena simpleks algoritma za rješavanje ekonomski optimiziranog problema kontrole proizvodnje. Metoda dinamičkog programiranja za izbor optimalnog profila kolosijeka. test, dodano 15.10.2010 Metode optimizacije za rješavanje ekonomskih problema. Klasična formulacija optimizacijskog problema. Optimizacija funkcija. Optimizacija funkcionalnosti. Višekriterijumska optimizacija. Metode za svođenje problema sa više kriterijuma na problem sa jednim kriterijumom. Metoda koncesija. sažetak, dodan 20.06.2005 Primjena metoda nelinearnog programiranja za rješavanje problema s nelinearnim funkcijama varijabli. Uvjeti optimalnosti (Kuhn-Tucker teorem). Metode uvjetne optimizacije (Wolfeova metoda); gradijent dizajn; kaznene i barijere funkcije. sažetak, dodan 25.10.2009 Pojam, definicija, isticanje osobina, mogućnosti i karakteristika postojećih problema višekriterijumske optimizacije i načini njihovog rješavanja. Proračun metode jednakog i najmanjeg odstupanja višekriterijumske optimizacije i njena primjena u praksi. seminarski rad dodan 21.01.2012 Osnovni koncepti modeliranja. Opći koncepti i definicija modela. Izjava o optimizacijskim problemima. Metode linearnog programiranja. Opšti i tipični zadatak u linearnom programiranju. Simpleksna metoda za rješavanje problema linearnog programiranja. 5.
Višedimenzionalna optimizacija
Linearno programiranje
Optimizacija
- to je svrsishodna aktivnost, koja se sastoji u postizanju najboljih rezultata pod odgovarajućim uslovima. Kvantitativna procjena optimiziranog kvaliteta se naziva kriterijum optimalnosti
ili ciljna funkcija
Može se napisati kao: (5.1)
gdje je x 1, x 2, ..., x n- neki parametri optimizacije objekta. Postoje dvije vrste problema optimizacije - bezuvjetni i uvjetni. Bezuslovni zadatak
optimizacija se sastoji u pronalaženju maksimuma ili minimuma realne funkcije (5.1) odnvaljane varijable i definiranje odgovarajućih vrijednosti argumenata. Problemi uslovne optimizacije
, ili problemi s ograničenjima, su oni u čijoj formulaciji se nameću ograničenja na vrijednosti argumenata u obliku jednakosti ili nejednakosti. Rješenje optimizacijskih problema u kojima je kriterij optimalnosti linearna funkcija nezavisnih varijabli (odnosno sadrži ove varijable u prvom stepenu) sa linearnim ograničenjima na njih je predmet linearno programiranje.
Riječ "programiranje" ovdje odražava krajnji cilj studije - određivanje optimalnog plana ili optimalnog programa, prema kojem se iz skupa mogućih varijanti procesa koji se proučava, bira najbolja, optimalna varijanta. Primjer
takav zadatak je optimalna distribucija sirovina
između različitih industrija uz maksimalnu cijenu proizvodnje. Neka se od dvije vrste sirovina prave dvije vrste proizvoda. Označimo: x 1, x 2 - broj jedinica proizvoda prve i druge vrste; c 1, c 2 – Jedinice proizvoda prve i druge vrste, respektivno. Tada će ukupni trošak svih proizvoda biti:
(5.2)
Kao rezultat proizvodnje, poželjno je da ukupni troškovi proizvodnje budu maksimizirani.R (x 1, x 2 ) Je li funkcija cilja u ovom problemu. b 1, b 2 - količina raspoloživih sirovina prve i druge vrste;a ij- broj jedinica i
-. vrsta sirovine potrebne za proizvodnju jedinicej-ti tip proizvoda. S obzirom da potrošnja datog resursa ne može premašiti njegovu ukupnu količinu, zapisujemo restriktivne uslove za resurse: (5.3)
Varijable x 1, x 2 takođe možemo reći da su nenegativni i da nisu beskonačni .: (5.4)
Među skupom rješenja sistema nejednačina (5.3) i (5.4) potrebno je pronaći takvo rješenje ( x 1, x 2 ) za koju je funkcijaRdostiže najveću vrijednost. U sličnom obliku formulisani su i tzv. transportni zadaci (zadaci optimalne organizacije isporuke robe, sirovina ili proizvoda iz različitih skladišta na više destinacija uz minimalne troškove transporta) i niz drugih. Grafička metoda za rješavanje problema linearnog programiranja.
Neka se traži da se pronađe x 1 i x 2 , zadovoljavajući sistem nejednakosti: (5.5)
i uslove nenegativnost:
(5.6)
za koja funkcija (5.
7
)
dostiže maksimum. Rješenje.
Iscrtajte u pravougaonom koordinatnom sistemu x 1 Vol 2 područje izvodljivih rješenja problema (slika 11). Za to, zamjenjujući svaku od nejednakosti (5.5) jednakošću, konstruišemo odgovarajući njemu granična linija: (i = 1, 2, … ,
r)
Rice. jedanaest Ova linija dijeli cijelu ravan na dvije poluravnine. Za koordinate x 1, x 2 bilo koju tačku A jednoj poluravni, vrijedi sljedeća nejednakost: i za koordinate bilo koje tačke V druga poluravnina je suprotna nejednakost: Koordinate bilo koje tačke granične linije zadovoljavaju jednačinu: Da bi se utvrdilo na kojoj strani granične linije se nalazi poluravnina koja odgovara datoj nejednakosti, dovoljno je "testirati" jednu tačku (najjednostavnija tačka je O(0; 0)). Ako je pri zamjeni njenih koordinata u lijevu stranu nejednakosti ona zadovoljena, tada se poluravnina okreće prema ispitnoj tački, ako nejednakost nije zadovoljena, tada se odgovarajuća poluravnina okreće u suprotnom smjeru. Smjer poluravnine prikazan je na crtežu šrafiranjem. nejednakosti: odgovaraju poluravni koja se nalazi desno od ordinate i iznad apscise. Na slici konstruišemo granične linije i poluravnine koje odgovaraju svim nejednačinama. Zajednički dio (presjek) svih ovih poluravni predstavljaće područje izvodljivih rješenja ovog problema. Prilikom konstruisanja oblasti izvodljivih rešenja, u zavisnosti od specifičnog tipa sistema ograničenja (nejednakosti) na varijable, može se javiti jedan od sledeća četiri slučaja: Rice. 12. Područje izvodljivih rješenja je prazno, što odgovara nekonzistentnosti sistema nejednačina; nema rješenja Rice. 13. Područje izvodljivih rješenja prikazano je jednom tačkom A, koja odgovara jedinom rješenju sistema Rice. 14. Područje izvodljivih rješenja je ograničeno, prikazano kao konveksan poligon. Postoji beskonačan skup izvodljivih rješenja Rice. 15. Područje izvodljivih rješenja je neograničeno, u obliku konveksnog poligonalnog područja. Postoji beskonačan skup izvodljivih rješenja Grafički prikaz funkcije cilja sa fiksnom vrijednošćuRdefiniše pravu liniju, a kada se mijenjaR- familija paralelnih linija sa parametromR. Za sve tačke koje leže na jednoj od pravih, funkcija R uzima jednu određenu vrijednost, stoga se ove linije nazivaju linije nivoa
za R funkciju. Vektor gradijenta:
okomitodo linija nivoa, pokazuje smjer porastaR.
Problem nalaženja optimalnog rješenja sistema nejednačina (5.5) za koji je ciljna funkcijaR(5.7) dostigne maksimum, geometrijski se svodi na određivanje u području dopuštenih rješenja tačke kroz koju prolazi linija nivoa koja odgovara najvećoj vrijednosti parametraR Rice. 16 Ako je područje izvodljivih rješenja konveksan poligon, onda je ekstremum funkcijeR
je postignut barem na jednom od vrhova ovog poligona. Ako je ekstremna vrijednostRse dostigne na dva vrha, tada se ista ekstremna vrijednost postiže u bilo kojoj tački na segmentu koji povezuje ova dva vrha. U ovom slučaju se kaže da postoji problem alternativni optimum
.
U slučaju neograničenog područja, ekstremum funkcijeRili ne postoji, ili se dostiže na jednom od vrhova regiona, ili ima alternativni optimum. Primjer.
Neka je potrebno pronaći vrijednosti x 1 i x 2 zadovoljavanje sistema nejednakosti: i uslove nenegativnost:
za koja funkcija: dostiže maksimum. Rješenje.
Svaku od nejednakosti zamjenjujemo jednakošću i konstruiramo granične linije: Rice. 17 Definirajmo poluravnine koje odgovaraju ovim nejednačinama "testiranjem" tačke (0; 0). Uzimajući u obzir nenegativnost x 1 i x 2 dobijamo oblast izvodljivih rešenja ovog problema u obliku konveksnog poligona OAVDE.
U području izvodljivih rješenja pronalazimo optimalno rješenje konstruiranjem vektora gradijenta pokazujućiuzlazni pravacR.
Optimalno rješenje odgovara tački V, čije se koordinate mogu odrediti grafički ili rješavanjem sistema od dvije jednadžbe koje odgovaraju graničnim linijama AB i VD: odgovor:
x 1 = 2; x 2 = 6; R max = 22.
Zadaci.
Odrediti položaj tačke ekstrema i ekstremnu vrijednost ciljne funkcije pod datim ograničenjima. Tabela 9 Extremum M sjekira Max ;
;
;
;




gdje je koeficijent. Uz to, uzmite u obzir i uslov konjugacije
ili
gdje
i uzimajući u obzir (6) i (7)
Izraz (10) je sistem linearnih algebarskih jednadžbi. Njegov korijen je još jedna aproksimacija rješenja
gdje Slični dokumenti
![]()


![]()
![]()

![]()
![]()
![]()




![]()
![]()


![]()
![]()


Ograničenja
![]() ;
; ![]() ;
;
![]() ; ;
; ;
![]() ;
;
;
;
;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;