Dom » Ostalo » Elementi mehanike kontinuuma i zakoni održanja. Elementi mehanike kontinuuma

Elementi mehanike kontinuuma i zakoni održanja. Elementi mehanike kontinuuma

PREDAVANJE br. 5 Elementi mehanike kontinuuma Fizički model: kontinualni medij je model materije, u okviru kojeg se zanemaruje unutrašnja struktura materije, pod pretpostavkom da je materija kontinuirano raspoređena po čitavom volumenu koji zauzima i da u potpunosti ispunjava ovaj volumen. Medij se naziva homogenim ako ima ista svojstva u svakoj tački. Izotropan je medij čija su svojstva ista u svim smjerovima. Agregatna stanja materije Čvrsto stanje je stanje materije koje karakteriše fiksni volumen i nepromjenjivost oblika. Tečnost je stanje supstance koju karakteriše fiksni volumen, ali nema određeni oblik. Gas je stanje tvari u kojem supstanca ispunjava cjelokupnu zapreminu koja joj se daje.

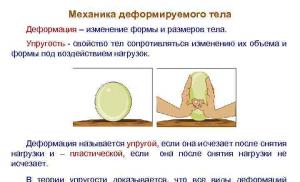
Mehanika deformabilnog tijela Deformacija je promjena oblika i veličine tijela. Elastičnost je svojstvo tijela da se odupru promjenama svog volumena i oblika pod utjecajem opterećenja. Deformacija se naziva elastičnom ako nestane nakon skidanja tereta i - plastičnom, ako ne nestane nakon skidanja opterećenja. U teoriji elastičnosti dokazano je da se sve vrste deformacija (zatezanje – kompresija, posmika, savijanje, torzija) mogu svesti na istovremeno nastajuće vlačno – kompresijske i posmične deformacije.

Vlačna - kompresijska deformacija Rastezanje - kompresija je povećanje (ili smanjenje) dužine cilindričnog ili prizmatičnog tijela uzrokovano silom usmjerenom duž njegove uzdužne ose. Apsolutna deformacija je vrijednost jednaka promjeni veličine tijela uzrokovanoj vanjskim utjecajima:, (5.1) gdje su l 0 i l početna i konačna dužina tijela. Hookeov zakon (I) (Robert Hooke, 1660): elastična sila je proporcionalna veličini apsolutne deformacije i usmjerena je prema njenom smanjenju:, (5.2) gdje je k koeficijent elastičnosti tijela.

Relativna deformacija:. (5.3) Mehanički napon je veličina koja karakterizira stanje deformiranog tijela = Pa:, (5.4) gdje je F sila koja uzrokuje deformaciju, S je površina poprečnog presjeka tijela. Hookeov zakon (II): Mehanički napon koji nastaje u tijelu proporcionalan je vrijednosti njegove relativne deformacije: [E] = Pa.

Deformacije čvrstih tijela poštuju Hookeov zakon do određene granice. Odnos između deformacije i naprezanja prikazan je u obliku dijagrama naprezanja, čiji se kvalitativni tok razmatra za metalnu šipku.

Energija elastične deformacije Pod zatezanjem – kompresijom, energija elastične deformacije, (5.8) gdje je V zapremina deformiranog tijela. Nasipna gustina napetosti - kompresije energije elastične deformacije na (5.9) Nasipna gustina posmične energije elastične deformacije (5.10) pri

Elementi mehanike tečnosti i gasova (hidro- i aeromehanika) Nalazeći se u čvrstom agregatnom stanju, telo istovremeno poseduje i elastičnost oblika i elastičnost zapremine (ili, što je isto, pri deformacijama u čvrstom telu, oboje normalno i nastaju tangencijalna mehanička naprezanja). Tečnosti i gasovi imaju samo zapreminsku elastičnost, ali nemaju elastičnost oblika (poprime oblik posude u kojoj se nalaze). Posljedica ove zajedničke osobine tekućina i plinova je kvalitativna sličnost većine mehaničkih svojstava tekućina i plinova, a njihova razlika su samo kvantitativne karakteristike (npr. gustoća tekućine je po pravilu veća od gustine gasa). Stoga se u okviru mehanike kontinuuma koristi jedinstven pristup proučavanju tekućina i plinova.

Početne karakteristike Gustoća tvari je skalarna fizička veličina koja karakterizira raspodjelu mase po volumenu tvari i određena je omjerom mase tvari sadržane u određenom volumenu i vrijednosti ovog volumena = m / kg 3. U slučaju homogene sredine, gustina supstance se izračunava po formuli (5.11) U opštem slučaju nehomogenog medija, masa i gustina supstance su povezane relacijom (5. 12) Pritisak je skalarna veličina koja karakteriše stanje tečnosti ili gasa i jednaka je sili koja deluje na jediničnu površinu u pravcu koji je normalan na nju [p] = Pa: (5.13)

Elementi hidrostatike Osobine sila koje djeluju unutar tečnosti (gasa) u mirovanju 1) Ako se unutar tečnosti koja miruje odvoji mala zapremina, tada tečnost vrši isti pritisak na ovu zapreminu u svim pravcima. 2) Tečnost koja miruje deluje na površinu čvrstog tela u dodiru sa njom silom usmerenom duž normale na ovu površinu.

Jednačina kontinuiteta Cijev za strujanje je dio tekućine omeđen strujnim linijama. Stacionarno (ili stabilno stanje) je tok fluida u kojem se oblik i lokacija strujnih linija, kao i vrijednosti brzina u svakoj tački pokretne tekućine, ne mijenjaju tokom vremena. Maseni protok tekućine je masa tekućine koja prolazi kroz poprečni presjek mlazne cijevi u jedinici vremena = kg/s:, (5.15) gdje su i v gustina i brzina strujanja tekućine u presjeku S.

Jednačina kontinuiteta je matematički odnos, prema kojem je, za stabilan tok tekućine, njegov maseni protok u svakom dijelu protočne cijevi isti:, (5.16)

Nestišljiva je tečnost čija gustina ne zavisi od temperature i pritiska. Volumetrijski protok tečnosti - zapremina tečnosti koja prolazi kroz poprečni presek protočne cevi u jedinici vremena = m 3 / s: u svakom delu strujne cevi je isti:, (5.18)

Viskoznost je svojstvo gasova i tečnosti da se odupru kretanju jednog dela u odnosu na drugi. Fizički model: idealna tekućina - zamišljena nestišljiva tekućina u kojoj nema viskoziteta i toplinske provodljivosti. Bernulijeva jednačina (Daniel Bernoulli 1738) je jednačina koja je posljedica zakona održanja mehaničke energije za stacionarni tok idealnog nestišljivog fluida i napisana je za proizvoljni dio cijevi za strujanje u gravitacijskom polju:. (5.19)

U Bernoullijevoj jednadžbi (5.19): p je statički pritisak (pritisak fluida na površini tela koje oblijeta oko njega; - dinamički pritisak; - hidrostatički pritisak.

Unutrašnje trenje (viskozitet). Newtonov zakon (Isaac Newton, 1686): sila unutrašnjeg trenja po jedinici površine pokretnih slojeva tekućine ili plina direktno je proporcionalna gradijentu brzine slojeva:, (5.20) gdje je koeficijent unutrašnje trenje (dinamički viskozitet), = m 2 / s.

Vrste strujanja viskoznog fluida Laminarni tok je oblik strujanja u kojem se tekućina ili plin kreću u slojevima bez miješanja i pulsiranja (to jest, slučajnih brzih promjena brzine i pritiska). Turbulentno strujanje je oblik strujanja tekućine ili plina, u kojem njihovi elementi vrše neuređena, nestabilna kretanja duž složenih putanja, što dovodi do intenzivnog miješanja između slojeva pokretne tekućine ili plina.

Reynoldsov broj Kriterijum za prelazak režima laminarnog strujanja u turbulentni režim zasniva se na upotrebi Reynoldsovog broja (O zbirci Reynoldsa, 1876-1883). U slučaju kretanja fluida kroz cijev, Reynoldsov broj se određuje kao, (5.21) gdje je v prosječna brzina fluida po dijelu cijevi; d - prečnik cevi; i - gustina i koeficijent unutrašnjeg trenja fluida. Pri vrijednostima Re 4000 - turbulentni način rada. Na vrijednosti od 2000

Laminarni tok viskoznog fluida u horizontalnoj cevi Razmotrimo tok viskoznog fluida, pozivajući se direktno na iskustvo. Pomoću gumenog crijeva spojite tanku horizontalnu staklenu cijev sa vertikalnim manometrijskim cijevima zalemljenim u nju na slavinu za vodu (vidi sliku). Pri malom protoku jasno je vidljivo smanjenje nivoa vode u manometrijskim cijevima u smjeru protoka (h 1> h 2> h 3). Ovo ukazuje na prisustvo gradijenta pritiska duž ose cevi - statički pritisak u tečnosti opada duž protoka.

Laminarni tok viskoznog fluida u horizontalnoj cevi U jednoličnom pravolinijskom toku fluida, sile pritiska su uravnotežene silama viskoziteta.

Distribucija brzina u poprečnom presjeku toka viskoznog fluida može se uočiti kada on teče iz vertikalne cijevi kroz uski otvor (vidi sliku). Ako, na primjer, sa zatvorenim ventilom K, prvo sipate neobojeni glicerin, a zatim pažljivo dodajte obojeni glicerin odozgo, tada će u ravnoteži sučelje D biti horizontalno. Ako se otvori slavina K, granica će poprimiti oblik sličan paraboloidu okretanja. Ovo ukazuje na postojanje raspodjele brzina u poprečnom presjeku cijevi s viskoznim protokom glicerola.

Poiseuilleova formula Raspodjela brzine u poprečnom presjeku horizontalne cijevi u laminarnom toku viskoznog fluida određena je formulom, (5.23) gdje su R i l polumjer i dužina cijevi, respektivno, p je razlika tlaka pri krajeva cijevi, r je udaljenost od ose cijevi. Volumetrijski protok tečnosti je određen Poiseuilleovom formulom (Jean Poiseuille, 1840): (5,24)

Kretanje tijela u viskoznoj sredini Kada se tijela kreću u tekućini ili plinu, na tijelo djeluje sila unutrašnjeg trenja, ovisno o brzini tijela. Pri malim brzinama uočava se laminarni tok tekućine ili plina oko tijela i ispostavlja se da je sila unutrašnjeg trenja proporcionalna brzini tijela i određena je Stokesovom formulom (George Stokes, 1851):, (5.25) gdje je b konstanta ovisno o obliku tijela i njegovoj orijentaciji u odnosu na tok, l je karakteristična veličina tijela. Za loptu (b = 6, l = R), sila unutrašnjeg trenja:, (5.26) gdje je R polumjer kuglice.

7.1. Opšta svojstva tečnosti i gasova. Kinematički opis kretanja fluida. Vektorska polja. Protok i cirkulacija vektorskog polja. Stacionarni tok idealnog fluida. Vodovi i cijevi struje. Jednačine kretanja i ravnoteže tečnosti. Jednačina kontinuiteta za nestišljivi fluid

Mehanika kontinuuma je grana mehanike posvećena proučavanju kretanja i ravnoteže gasova, tečnosti, plazme i deformabilnih čvrstih tela. Glavna pretpostavka mehanike kontinuuma je da se materija može smatrati neprekidnim kontinuiranim medijem, zanemarujući njenu molekularnu (atomsku) strukturu, a u isto vrijeme, raspodjela svih njenih karakteristika (gustina, naprezanja, brzine čestica) u mediju može smatrati kontinuiranim.

Tečnost je supstanca u kondenzovanom stanju, između čvrstog i gasovitog. Područje postojanja tekućine ograničeno je sa strane niskih temperatura faznim prijelazom u čvrsto stanje (kristalizacija), a sa strane visokih temperatura - u plinovito stanje (isparavanje). Kada se proučavaju svojstva neprekidnog medija, sam medij se predstavlja kao da se sastoji od čestica čije su veličine mnogo veće od veličine molekula. Dakle, svaka čestica sadrži ogroman broj molekula.

Da biste opisali kretanje fluida, možete odrediti položaj svake čestice fluida kao funkciju vremena. Ovaj način opisivanja razvio je Lagrange. Ali možete pratiti ne čestice tečnosti, već pojedinačne tačke u prostoru, i primetiti brzinu kojom pojedine čestice tečnosti prolaze kroz svaku tačku. Drugi način se zove Ojlerova metoda.

Stanje kretanja fluida se može odrediti specificiranjem za svaku tačku u prostoru vektor brzine kao funkciju vremena.

Zbirka vektora , dat za sve tačke u prostoru, formira polje vektora brzine, koje se može prikazati na sledeći način. Nacrtajmo linije u fluidu koji se kreće tako da se tangenta na njih u svakoj tački poklapa u smjeru s vektorom (Slika 7.1). Ove linije se nazivaju strujne linije. Dogovorimo se da nacrtamo strujne linije tako da njihova gustina (omjer broja linija
na veličinu površine koja je okomita na njih
kroz koji prolaze) bio je proporcionalan veličini brzine na datoj lokaciji. Tada će, iz uzorka strujnih linija, biti moguće procijeniti ne samo smjer, već i veličinu vektora na različitim tačkama u prostoru: tamo gde je brzina veća, strujne linije će biti gušće.

Broj strujnih vodova koji prolaze kroz lokaciju
okomito na strujne linije je
, ako je lokacija proizvoljno orijentirana na strujne linije, broj strujnih linija je gdje je
- ugao između smjera vektora i normalno za sajt ... Često se koristi notacija
... Broj strujnih linija na stranici konačna veličina određena je integralom:
... Integral ove vrste naziva se tok vektora preko stranice .

V Veličina i smjer vektora mijenja se tokom vremena, stoga, linija linija ne ostaje konstantna. Ako u svakoj tački u prostoru vektor brzine ostaje konstantan po veličini i smjeru, tada se tok naziva stacionarnim ili stacionarnim. U stacionarnom toku, bilo koja čestica tečnosti prolazi kroz datu tačku u prostoru istom brzinom. Obrazac strujne linije u ovom slučaju se ne mijenja, a strujne linije se poklapaju s putanjama čestica.

Protok vektora kroz određenu površinu i kruženje vektora duž date konture omogućavaju suđenje prirode vektorskog polja. Međutim, ove vrijednosti daju prosječnu karakteristiku polja unutar zapremine zatvorene površinom kroz koju se određuje strujanje, ili u blizini konture duž koje se odvija cirkulacija. Smanjenjem veličine površine ili konture (povlačenjem do tačke), možete doći do vrijednosti koje će karakterizirati vektorsko polje u datoj tački.

Razmotrimo polje vektora brzine nestišljivog kontinuiranog fluida. Protok vektora brzine kroz određenu površinu jednak je volumenu tekućine koja teče kroz ovu površinu u jedinici vremena. Gradimo u blizini tačke R imaginarne zatvorene površine S(Slika 7.2) . Ako je u obimu V ograničena površinom, tečnost ne nastaje i ne nestaje, tada će protok prema van kroz površinu biti jednak nuli. Razlika protoka od nule će ukazati da unutar površine postoje izvori ili ponori tečnosti, odnosno tačke u kojima tečnost ulazi u zapreminu (izvori) ili se uklanja iz zapremine (ponori). Brzina protoka određuje ukupnu snagu izvora i sudopere. Uz prevlast izvora nad efluentima, protok je pozitivan, sa prevlašću efluenta - negativan.

Kvocijent dijeljenja protoka sa količinom zapremine iz koje teče protok,
, je prosječna specifična snaga izvora uključenih u volumen V.Što je volumen manji V, uključujući tačku R,što je ovaj prosjek bliži stvarnoj gustini snage u toj tački. U limitu na
, tj. kada sažimamo zapreminu na tačku, dobijamo pravu specifičnu snagu izvora u tački R, zove se divergencija (divergencija) vektora :
... Rezultirajući izraz vrijedi za bilo koji vektor. Integracija se vrši preko zatvorene površine S, ograničavajući obim V... Divergencija je određena ponašanjem vektorske funkcije blizu tačke R. Divergencija je skalarna funkcija koordinata koje definiraju n pozicija tačke R u svemiru.

Nađimo izraz za divergenciju u Dekartovom koordinatnom sistemu. Razmotrite u blizini tačke P (x, y, z) mali volumen u obliku paralelepipeda sa ivicama paralelnim sa koordinatnim osa (slika 7.3). S obzirom na malenost volumena (težit ćemo ka nuli), vrijednosti
unutar svake od šest lica paralelepipeda može se smatrati nepromijenjenim. Protok preko cijele zatvorene površine formira se od tokova koji teku kroz svaku od šest strana posebno.

Nađimo protok kroz par lica okomitih na graničnik NS na slici 7.3 lica 1 i 2) . Vanjski normalan lice 2 poklapa se sa smjerom ose NS... Zbog toga
a protok kroz lice 2 je
.Normalno ima smjer suprotan od osi NS. Vektorske projekcije po osi NS i na normalno imaju suprotne predznake,
, a protok kroz lice 1 je
... Ukupan protok u pravcu NS je jednako sa
... Razlika
je prirast kada se pomjeri duž ose NS on
... Zbog malenkosti

... Onda dobijamo
... Slično, kroz parove lica okomitih na osi Y i Z, tokovi su jednaki
i
... Potpuni protok kroz zatvorenu površinu. Podijeli ovaj izraz na
, naći divergenciju vektora u tački R:

Poznavanje vektorske divergencije u svakoj tački u prostoru, možete izračunati fluks ovog vektora kroz bilo koju površinu konačnih dimenzija. Da bismo to učinili, podijelimo volumen ograničen površinom S, u beskonačno veliki broj beskonačno malih elemenata
(Slika 7.4).

Za bilo koji element
vektor toka kroz površinu ovog elementa je
... Zbrajanje svih elemenata
, dobijamo protok kroz površinu S ograničavanje jačine zvuka V:
, integracija se vrši na volumenu V, ili

NS zatim Ostrogradski - Gaussova teorema. Evo
,je jedinični vektor normale na površinu dS na ovom mjestu.

Vratimo se na tok nestišljivog fluida. Napravimo konturu ... Zamislite da smo nekako trenutno zamrznuli tečnost u cijelom volumenu, s izuzetkom vrlo tankog zatvorenog kanala konstantnog poprečnog presjeka, koji uključuje konturu (Slika 7.5). U zavisnosti od prirode toka, tečnost u formiranom kanalu će biti ili stacionarna ili će se kretati (kružiti) duž konture u jednom od mogućih smerova. Kao mjera ovog kretanja, odabrana je vrijednost jednaka proizvodu brzine fluida u kanalu i dužine kruga,
... Ova veličina se naziva cirkulacija vektora duž konture (pošto kanal ima konstantan poprečni presjek i modul brzine se ne mijenja). U trenutku stvrdnjavanja zidova, za svaku česticu tekućine u kanalu, komponenta brzine okomita na zid će se ugasiti, a ostat će samo komponenta tangentna na konturu. Uz ovu komponentu je povezan impuls
, čiji je modul za česticu tečnosti zatvorenu u kanal dužine
, je jednako
, gdje - gustina tečnosti, - kanalna sekcija. Tečnost je idealna - nema trenja, tako da djelovanje zidova može samo promijeniti smjer
, njegova vrijednost će ostati konstantna. Interakcija između čestica tekućine će uzrokovati takvu preraspodjelu količine gibanja između njih, koja će izjednačiti brzine svih čestica. U ovom slučaju, algebarski zbir impulsa je, dakle, očuvan
, gdje - brzina cirkulacije, - tangencijalna komponenta brzine fluida u zapremini
u trenutku koji prethodi stvrdnjavanju zidova. Podjela na
, dobiti
.

C Cirkulacija karakteriše svojstva polja usrednjena za oblast sa dimenzijama reda prečnika konture ... Da bi se dobila karakteristika polja u tački R, morate smanjiti veličinu konture, povlačeći je do točke R... U ovom slučaju, granica cirkulacijskog odnosa vektora uzima se kao karakteristika polja na ravnoj konturi ugovaranje do tačke R, na veličinu konturne ravni S:
... Vrijednost ove granice ne ovisi samo o svojstvima polja u tački R, ali i na orijentaciju konture u prostoru, koja se može specificirati smjerom pozitivne normale na ravninu konture (normala povezana sa smjerom prelaska konture po pravilu desnog zavrtnja smatra se pozitivnom). Određivanje ove granice za različite smjerove , dobićemo njegove različite vrijednosti, a za suprotne normalne smjerove ove vrijednosti se razlikuju po predznaku. Za određeni smjer normale, vrijednost granice će biti maksimalna. Dakle, vrijednost granice se ponaša kao projekcija nekog vektora na smjer normale na ravan konture duž koje se odvija cirkulacija. Maksimalna vrijednost granice određuje modul ovog vektora, a smjer pozitivne normale na kojoj se postiže maksimum daje smjer vektora. Ovaj vektor se naziva rotor ili vrtlog vektora :
.

Da biste pronašli projekciju rotora na osu kartezijanskog koordinatnog sistema, morate odrediti granične vrijednosti za takve orijentacije mjesta S pri čemu je normalno do lokacije poklapa se s jednom od osi X, Y, Z. Ako, na primjer, pošaljete duž ose NS, nađi
... Circuit koji se u ovom slučaju nalazi u ravni paralelnoj sa YZ, uzmite konturu u obliku pravokutnika sa stranicama
i
... At
značenje i na svakoj od četiri strane konture može se smatrati nepromijenjenim. Dio 1 konture (slika 7.6) je suprotan osi Z, dakle na ovoj stranici poklapa se sa
, u odjeljku 2
, na lokaciji 3
, na lokaciji 4
... Za cirkulaciju duž ovog kola dobijamo vrijednost: . Razlika
je prirast kada se preseli Y on
... Zbog malenkosti
ovaj prirast se može predstaviti kao
.Isto tako, razlika
. Zatim cirkulacija duž razmatrane konture
,

gdje
- contour area. Podjela cirkulacije na
, nalazimo projekciju rotora na osa NS:
. Isto tako,
,
... Zatim rotor vektora definisan izrazom:

+
,

ili
.

Z rotor vektora u svakoj tački neke površine S, možemo izračunati cirkulaciju ovog vektora duž konture ograničavanje površine S... Da bismo to učinili, podijelimo površinu na vrlo male elemente
(Slika 7.7). Cirkulacija duž granice
je jednako sa
, gdje - pozitivna normala na element
. Zbrajanje ovih izraza na cijeloj površini S i zamenivši izraz za cirkulaciju, dobijamo
... Ovo je Stokesova teorema.

Dio fluida omeđen strujnim linijama naziva se strujna cijev. Vector , budući da je u svakoj tački tangenta na strujnu liniju, bit će tangentna na površinu potočne cijevi, a čestice fluida ne prelaze zidove potočne cijevi.

Razmotrimo poprečni presjek potočne cijevi okomit na smjer brzine S(Slika 7.8.). Pretpostavićemo da je brzina čestica tečnosti ista u svim tačkama ovog odseka. Tokom
kroz sekciju S proći će sve čestice čija je udaljenost u početnom trenutku ne prelazi vrijednost
... Dakle, tokom vremena
kroz sekciju S
, i po jedinici vremena kroz dionicu S zapremina tečnosti će proći, jednaka
.. Pretpostavimo da je strujna cijev toliko tanka da se brzina čestica u svakom njenom dijelu može smatrati konstantnom. Ako je fluid nestišljiv (tj. njegova gustina je svuda ista i ne menja se), tada količina tečnosti između sekcija i (Slika 7.9.) će ostati nepromijenjena. Zatim količine tekućine koje teče u jedinici vremena kroz sekcije i mora biti isti:

Dakle, za nestišljiv fluid, količina
u bilo kojem dijelu iste protočne cijevi mora biti isti:

.Ova izjava se zove teorema o kontinuitetu mlaza.

Kretanje idealnog fluida opisuje se Navier-Stokesovom jednačinom:

gdje t- vrijeme, x, y, z- koordinate čestice tečnosti,

- projekcije tjelesne sile, R- pritisak, ρ - gustina medijuma. Ova jednadžba vam omogućava da odredite projekciju brzine čestice medija kao funkciju koordinata i vremena. Da bi se sistem zatvorio, jednačina kontinuiteta se dodaje Navier-Stokesovoj jednačini, koja je posljedica teoreme o kontinuitetu mlaza:

... Za integraciju ovih jednačina potrebno je postaviti početne (ako kretanje nije stacionarno) i granične uslove.

Plan

1. Elementi mehanike kontinuuma. Stacionarno kretanje idealnog fluida. Bernulijeva jednačina.

2. Elastični naponi. Hookeov zakon.

Sažeci

1. Zapremina plina određena je zapreminom posude koju plin zauzima. U tečnostima, za razliku od gasova, prosečna udaljenost između molekula ostaje praktično konstantna, stoga tečnost ima praktično nepromenjenu zapreminu. U mehanici, sa visokim stepenom tačnosti, tečnosti i gasovi se smatraju neprekidnim, neprekidno raspoređenim u delu prostora koji zauzimaju. Gustina tečnosti malo zavisi od pritiska. Gustina gasova značajno zavisi od pritiska. Iz iskustva je poznato da se kompresibilnost tečnosti i gasa u mnogim problemima može zanemariti i koristiti jedinstveni koncept nestišljive tečnosti, čija je gustina svuda ista i ne menja se tokom vremena. Idealna tečnost - fizička apstrakcija, odnosno imaginarni fluid u kojem nema unutrašnjih sila trenja. Idealna tekućina je zamišljena tekućina u kojoj nema unutrašnjih sila trenja, a viskozna tekućina joj je u suprotnosti. Fizička veličina određena normalnom silom koja djeluje sa strane tekućine po jedinici površine naziva se tlak R tečnosti... Jedinica za pritisak je paskal (Pa): 1 Pa je jednak pritisku koji stvara sila od 1 N, ravnomerno raspoređena po površini koja je normalna na nju sa površinom od 1 m 2 (1 Pa = 1 N / m 2). Pritisak na bilo kojem mjestu fluida koji miruje je isti u svim smjerovima, a pritisak se jednako prenosi na cijelu zapreminu koju zauzima fluid u mirovanju.

Pritisak se linearno mijenja sa visinom... Pritisak P = rgh naziva se hidrostatskim. Sila pritiska na donje slojeve tečnosti je veća nego na gornje, stoga na telo uronjeno u tečnost deluje sila uzgona, određena Arhimedov zakon: na tijelo uronjeno u tečnost (gas) sa strane te tečnosti deluje sila uzgona prema gore, jednaka težini tečnosti (gasa) koju je istisnulo telo, gde je r gustina tečnosti, V- zapremina tela uronjenog u tečnost.

Kretanje fluida naziva se strujanje, a sakupljanje čestica fluida koji se kreće naziva se strujanje. Grafički je kretanje fluida prikazano pomoću strujnih linija, koje su nacrtane tako da se tangente na njih poklapaju u pravcu sa vektorom brzine fluida u odgovarajućim tačkama u prostoru (slika 45). Po obrascu strujnih linija može se suditi o smjeru i modulu brzine u različitim tačkama u prostoru, odnosno može se odrediti stanje kretanja fluida. Dio tekućine omeđen strujnim linijama naziva se strujna cijev. Protok tekućine naziva se stacionarnim (ili stacionarnim) ako se oblik i lokacija strujnih linija, kao i vrijednosti brzina u svakoj od njegovih točaka, ne mijenjaju tijekom vremena.

Razmislite o strujnoj cijevi. Odaberimo dva njegova odjeljka S 1 i S 2 , okomito na pravac brzine (Sl. 46). Ako je fluid nestišljiv (r = const), onda kroz sekciju S 2 će za 1 s proći istu zapreminu tečnosti kao kroz sekciju S 1, tj. Proizvod brzine protoka nestišljivog fluida i poprečnog presjeka protočne cijevi je konstantna vrijednost za datu protočnu cijev. Omjer se naziva jednačina kontinuiteta za nestišljiv fluid. - Bernulijeva jednačina - izraz zakona održanja energije u odnosu na stacionarni tok idealnog fluida (ovdje p - statički pritisak (pritisak fluida na površinu tela koje ga oblijeće), vrednost - dinamički pritisak, - hidrostatički pritisak). Za horizontalnu strujnu cijev, Bernoullijeva jednačina se zapisuje kao , gdje lijeva strana naziva se ukupni pritisak. Toricellijeva formula je napisana:

Viskoznost je svojstvo stvarnih fluida da se odupru kretanju jednog dela tečnosti u odnosu na drugi. Kada se neki slojevi prave tečnosti pomeraju u odnosu na druge, nastaju sile unutrašnjeg trenja, usmerene tangencijalno na površinu slojeva. Sila unutrašnjeg trenja F je veća, što je veća površina sloja S koji se razmatra, i zavisi od toga koliko se brzo menja brzina protoka fluida tokom prelaska sa sloja na sloj. Vrijednost Dv / Dx pokazuje koliko se brzo mijenja brzina pri prelasku od sloja do sloja u smjeru NS, okomito na smjer kretanja slojeva, a naziva se gradijent brzine. dakle, modul sile unutrašnjeg trenja je jednak, pri čemu je koeficijent proporcionalnosti h , ovisno o prirodi tekućine naziva se dinamička viskoznost (ili jednostavno viskoznost). Jedinica viskoziteta- paskal sekunda (Pa s) (1 Pa s = 1 N s / m 2). Što je viskozitet veći, to se tekućina više razlikuje od idealne, u njoj nastaju veće sile unutrašnjeg trenja. Viskoznost ovisi o temperaturi, a priroda ove ovisnosti za tekućine i plinove je različita (za tekućine opada s povećanjem temperature, za plinove, naprotiv, raste), što ukazuje na razliku u mehanizmima unutrašnjeg trenja. Viskoznost ulja posebno zavisi od temperature. Metode za određivanje viskoznosti:

1) Stokesova formula ; 2) Poiseuilleova formula

2. Deformacija se naziva elastičnom ako tijelo nakon prestanka djelovanja vanjskih sila poprimi svoju prvobitnu veličinu i oblik. Deformacije koje traju u tijelu nakon prestanka vanjskih sila nazivaju se plastične. Sila po jedinici površine poprečnog presjeka naziva se naprezanje i mjeri se u paskalima. Kvantitativna mjera koja karakterizira stepen deformacije koju doživljava tijelo je njegova relativna deformacija. Relativna promjena dužine šipke (uzdužna deformacija), relativna poprečna napetost (kompresija), gdje je d - prečnik šipke. Deformacije e i e " uvijek imaju različite predznake, gdje je m pozitivan faktor u zavisnosti od svojstava materijala, nazvan Poissonov omjer.

Robert Hooke je eksperimentalno otkrio da su za male deformacije, izduženje e i napon s direktno proporcionalni jedno drugom:, gdje je koeficijent proporcionalnosti E- Youngov modul.

Youngov modul je određen naprezanjem koje uzrokuje jedinično istezanje. Onda Hookeov zakon može se napisati ovako , gdje k- koeficijent elastičnosti: izduženje štapa pod elastičnom deformacijom proporcionalno je sili koja djeluje na štap. Potencijalna energija elastično rastegnutog (stisnutog) štapa Deformacije čvrstih tijela poštuju Hookeov zakon samo za elastične deformacije. Odnos između naprezanja i stresa je predstavljen kao dijagrami naprezanja(sl. 35). Iz slike se vidi da je linearna zavisnost s (e), koju je ustanovio Hooke, ispunjena samo u vrlo uskim granicama do tzv. granice proporcionalnosti (s p). Uz daljnje povećanje naprezanja, deformacija je i dalje elastična (iako ovisnost s (e) više nije linearna) i ne nastaju zaostale deformacije do granice elastičnosti (s y). Zaostale deformacije se javljaju u tijelu izvan granice elastičnosti, a graf koji opisuje povratak tijela u prvobitno stanje nakon prestanka djelovanja sile se ne prikazuje kao kriva IN, i paralelno sa njim - CF. Napon pri kojem se pojavljuje primjetna trajna deformacija (~ = 0,2%) naziva se granica tečenja (s t) - tačka WITH na krivini. Na području CD deformacija se povećava bez povećanja naprezanja, odnosno tijelo takoreći "teče". Ovo područje se naziva područje tečenja (ili područje plastične deformacije). Materijali za koje je područje popuštanja značajno nazivaju se viskoznim, za koje praktično nema - krhki. Uz dalje istezanje (po bod D) dolazi do uništenja organizma. Maksimalni stres koji se javlja u tijelu prije kvara je krajnja snaga (s p).

Predavanje 4. Elementi mehanike kontinuuma

Razmotrimo kretanje idealnog fluida - kontinuiranog medija čija se kompresibilnost i viskozitet mogu zanemariti. Odaberimo u njemu određeni volumen, u čijim se nekoliko tačaka određuju vektori brzine kretanja čestica tekućine u trenutku vremena. Ako slika vektorskog polja ostane nepromijenjena tokom vremena, tada se takvo kretanje fluida naziva stabilno stanje. U ovom slučaju, putanje čestica su neprekidne linije koje se ne seku. Oni se nazivaju streamlines i zapreminu tečnosti, ograničenu strujnim linijama, strujna cijev (slika 4.1).

Pošto čestice tečnosti ne prelaze površinu takve cevi, ona se može smatrati pravom cevi sa zidovima koji su pričvršćeni za tečnost. Odaberimo u strujnoj cijevi proizvoljne presjeke i okomite na smjer brzine čestica u sekcijama i, respektivno (slika 4.1).

U kratkom vremenskom periodu, zapremine tečnosti protiču kroz ove sekcije

. (4.1)

Dakle, tečnost je nestišljiva i. A onda, za bilo koji dio cijevi toka, jednakost

. (4.2)

Slika 4.1

Zove se jednačina kontinuiteta mlaza. U skladu sa (4.2), gdje je poprečni presjek manji, brzina protoka fluida je veća i obrnuto.

Bernulijeva jednačina.Neka su razmatrani presjeci protočne cijevi idealnog fluida mali, tako da se vrijednosti brzine i pritiska u njima mogu smatrati konstantnim, tj. i, u preseku i, u (sl. 4.2).

Kada se fluid kreće u kratkom vremenskom periodu, sekcija će se pomeriti u poziciju koja je prešla putanju, a sekcija će se pomeriti u poziciju koja je prošla. Zapremina tečnosti zatvorena između sekcija i zbog jednačine kontinuiteta će biti

jednak je zapremini tečnosti sadržane u intervalu

Rice. 4.2 između i. Cijev ima određeni nagib

i centri njegovih presjeka i nalaze se na visinama i iznad datog

horizontalni nivo. Uzimajući u obzir to i, promjena ukupne energije odabrane mase tekućine koja se nalazi u početnom trenutku između sekcija i može se predstaviti u obliku

. (4.3)

Ova promjena, prema zakonu održanja energije, je posljedica rada vanjskih sila. U ovom slučaju, to su sile pritiska i, koje djeluju na presjeke i gdje su odgovarajući pritisci. Za bilo koji dio strujne cijevi

, (4.4)

gdje je gustina fluida Jednakost (4.4) izražava osnovni zakon hidrodinamike, koji se naziva i Bernulijeva jednačina po imenu naučnika koji ju je prvi put primio.

Pritisak u protoku fluida.Treba napomenuti da u izrazu (4.4) svi pojmovi imaju dimenziju pritiska i prema tome se nazivaju: - dinamički, - hidrostatički ili težinski, - statički pritisak, a njihov zbir je ukupan pritisak. Uzimajući ovo u obzir, relacija (4.4) se može izraziti riječima: u stacionarnom strujanju idealnog fluida, ukupni tlak u bilo kojem dijelu potočne cijevi (u granici strujne linije) je konstantna vrijednost, a brzina protoka

. (4.5)

Istjecanje tečnosti iz rupe.Neka rupa koja se nalazi blizu dna posude napunjena tečnošću bude otvorena (slika 4.3). Odaberimo protočnu cijev s poprečnim presjecima - na nivou otvorene površine tekućine u posudi; - u nivou rupe -. Za njih Bernoullijeva jednačina ima oblik

. (4.6)

Evo, gde je atmosferski pritisak. Dakle, iz (4.6) imamo

(4.7)

Ako, onda član može biti

Rice. 4.3 zanemareno. Tada iz (4.7) dobijamo

Prema tome, brzina protoka fluida će biti jednaka:

, (4.8)

gdje. Formulu (4.8) je prvi dobio Torricelli i nosi njegovo ime. U kratkom vremenskom periodu iz posude istječe količina tečnosti. Odgovarajuća masa, gdje je gustina tečnosti. Ona ima zamah. Shodno tome, posuda daje ovaj impuls izlaznoj masi, tj. deluje nasilno

Prema trećem Newtonovom zakonu, na plovilo će djelovati sila, tj.

. (4.9)

Ovdje je sila reakcije tekućine koja teče. Ako je plovilo na kolicima, tada će se pod djelovanjem sile početi kretati, što se naziva reaktivno kretanje.

Laminarni i turbulentni tokovi. Viskoznost.Protok tekućine, u kojem svaki od njegovih slojeva klizi u odnosu na druge slične slojeve, a nema miješanja, naziva selaminarni ili slojeviti... Ako se unutar tekućine formiraju vrtlozi i slojevi se intenzivno miješaju, tada se takvo strujanje naziva turbulentno.

Stacionarni (stacionarni) tok idealnog fluida je laminaran pri bilo kojoj brzini. U stvarnim fluidima između slojeva nastaju sile unutrašnjeg trenja, tj. prave tečnosti su viskozne. Stoga svaki od slojeva usporava kretanje susjednog sloja. Veličina sile unutrašnjeg trenja proporcionalna je kontaktnoj površini slojeva i gradijentu brzine, tj.

, (4.10)

gdje je koeficijent proporcionalnosti, nazvan koeficijent viskoznosti. Njegova jedinica je (paskal-sekunda). Viskoznost zavisi od vrste tečnosti i temperature. Kako temperatura raste, viskoznost se smanjuje.

Ako je sila unutrašnjeg trenja mala, a protok mali, tada je kretanje praktično laminarno. Pri velikim silama unutrašnjeg trenja narušava se slojevita priroda strujanja, počinje intenzivno miješanje, tj. dolazi do prelaska u turbulenciju. Uvjeti za ovaj prijelaz u protoku tekućine kroz cijevi određuju se vrijednošću cr pozvan Reynoldsov broj

, (4.11)

gdje je gustina tečnosti, prosječna brzina protoka po dijelu cijevi i prečnik cijevi. Eksperimenti pokazuju da kada je tok laminaran, kada postaje turbulentan. Za cijevi s kružnim poprečnim presjekom radijusa, Reynoldsov broj. Utjecaj viskoznosti dovodi do činjenice da se pri brzini protoka kroz cijev kružnog poprečnog presjeka različiti slojevi razlikuju. Određuje se njegova prosječna vrijednostpo Poiseuilleovoj formuli

, (4.12)

gdje je polumjer cijevi, () razlika tlaka na krajevima cijevi, njena dužina.

Efekat viskoznosti se takođe detektuje kada strujanje stupi u interakciju sa stacionarnim telom. Obično, u skladu sa mehaničkim principom relativnosti, razmatra se inverzni problem, npr. Stokes utvrđeno je da na lopticu koja se kreće u tekućini djeluje sila trenja

, (4.13)

gdje je r - radijus lopte, - brzina njenog kretanja. Stokes formula (4.13) se u laboratorijskoj praksi koristi za određivanje koeficijenta viskoznosti tečnosti.

Oscilacije i talasi

Oscilatorno kretanje ili jednostavno oscilacija je kretanje koje karakterizira jedan ili drugi stupanj ponavljanja u vremenu vrijednosti fizičkih veličina koje određuju ovo kretanje. Oscilacije susrećemo u proučavanju najrazličitijih fizičkih pojava: zvuk, svjetlost, naizmjenične struje, radio valovi, njihanje klatna itd. Unatoč širokoj raznolikosti oscilatornih procesa, svi se oni odvijaju prema nekim zajedničkim zakonima za njih. Najjednostavniji od njih je harmonijsko oscilatorno kretanje. Oscilatorno kretanje se naziva harmonijskim ako se promijeni fizička veličina NS (pomjeranje) se događa prema kosinusnom (ili sinusnom) zakonu

, (4.14)

gdje je vrijednost A - jednak maksimalnom pomaku NS sistema iz ravnotežnog položaja, naziva se amplituda oscilacije, (, određuje veličinu pomaka x u datom trenutku i naziva se faza oscilacije. jednaka broju potpunih oscilacija koje se dešavaju tokom vrijeme s.

Period je vrijeme jednog punog zamaha. Ona je povezana sa cikličnom frekvencijom slijedećim odnosom

. (4.15)

Očigledno je da je linearna frekvencija (broj oscilacija po jedinici vremena) povezana sa periodom T na sledeći način

(4.16)

Jedinica frekvencije je frekvencija takve oscilacije, čiji je period 1 s. Ova jedinica se zove herc (Hz). Učestalost na 10 3 Hz se naziva kiloherc (kHz), na 10 6 Hz, megaherc (MHz).

Oscilatorno kretanje karakteriše ne samo pomeranje NS, ali i brzinom i ubrzanjem a. Njihove vrijednosti se mogu odrediti iz izraza (4.14).

Diferencirajući (4.14) s obzirom na vrijeme, dobijamo formulu brzine

. (4.17)

Kao što se vidi iz (4.17), brzina se takođe menja po harmonijskom zakonu, a amplituda brzine je jednaka. Iz poređenja (4.14) i (4.17) slijedi da je brzina ispred pomaka faze za.

Ponovo diferencirajući (4.14) u vremenu, nalazimo izraz za ubrzanje

. (4.18)

Kao što slijedi iz (4.14) i (4.18), ubrzanje i pomak su u antifazi. To znači da u trenutku kada pomak dostigne najveću pozitivnu vrijednost, ubrzanje dostiže najveću negativnu vrijednost, i obrnuto.

Ravan Traveling Wave Equation

Talasna jednadžbase naziva izraz koji opisuje glavu i Jednostavnost pomaka oscilirajuće čestice iz koordinata i vremena:

. (4.20)

Neka tačke koje se nalaze u ravni osciliraju u skladu sa zakonom. Oscilacije čestica medija u tački (slika 4.4) koja se nalazi na udaljenosti ja sam od izvora oscilacija će nastati prema istom a u pitanju, ali će zaostajati za fluktuacijama izvora i ka on (gdje je brzina prostiranja talasa). Jednačina za vibraciju ovih čestica je: (4.20)

Slika 4.4

Budući da je tačka odabrana proizvoljno, tada jednadžba (5.7) omogućava da odredite pomak bilo koje tačke medija uključene u oscilatorni proces u bilo kojem trenutku, stoga se nazivajednadžba aviona koji putuje l mi. U opštem slučaju, ima oblik:

(4.21)

gdje je amplituda talasa; - faza ravnog talasa; ciklična talasna frekvencija; početna faza oscilovanja a niy.

Zamjenjujući u jednačinu (4.21) izraze za brzinu () i cikličku frekvenciju (), n dobićemo:

(4.22)

Ako uvedemo talasni broj, onda se jednačina ravnog talasa može napisati u obliku:

. (4.23)

Brzina u ovim jednačinama je ck O brzina kretanja faze talasa, a naziva sefazna brzina... Zaista, neka je faza konstantna u talasnom procesu... Da bismo pronašli brzinu njenog kretanja, izraz za fazu dijelimo i razlikujemo po vremenu e ni. Dobijamo:

Gdje.

Stojeći talas. Ako se nekoliko valova istovremeno širi u mediju, ondaprincip superpozicije (superpozicija): do a val čekanja ponaša se kao da nema drugih valova i rezultat NS pomicanje čestica medija u bilo kojem trenutku je jednako geometrijskom zbroju pomaka koji se dobivaju frekvencijom i učestvujući u svakoj od komponenti talasnih procesa sa sovama.

Od velikog praktičnog interesa je superpozicija dva ravna talasa

I, (4.24)

sa istim frekvencijama i amplitudama, šireći se jedna prema drugoj duž ose. Dodajući ove jednačine, n O dobijamo jednačinu rezultujućeg talasa, tzv stojeći talas (4.25)

Tabela 4.1

U putujućem talasu	U stajaćem talasu
Amplituda vibracija
Sve tačke okoline fluktuiraju sa istim yi amp i tud ami	Sve tačke okoline fluktuiraju sa različitim a m sa pločama
Faza oscilovanja
Faza oscilovanja zavisi od koordinata. i izmjerena tačka	Sve tačke između dva čvora vibriraju u istoj fazi e ... Prilikom prolaska kroz čvor, faza se računa e bania se mijenja u.
Prijenos energije
Energija vibracionog kretanja prenosi se u pravcu distribucije O lutajući talasi.	Nema prijenosa energije, samo unutar granica postoje međusobne transformacije energije.

Na tačkama medijuma, gde ampl i tamo talasi postaju nula (). Ove tačke se nazivajučvorovi () stojeći val. Koordinate čvorova.

Udaljenost između dva susjedna čvora (ili između dva s O sedlasti antinodi), tzvstajaća talasna dužina,jednaka polovini dužine trčanja ona maše ... Dakle, kada se dodaju dva putujuća talasa, formira se stojni talas čiji su čvorovi i antičvorovi sve vreme na istim mestima.

Karakteristike putujućih i stajaćih valova date su u tabeli 5.1.

Main 1 , 5 . 6

Dodati. 18, 22 [25-44]

Kontrolna pitanja:

Main osamnaest .

Kontrolna pitanja:

1. Može li pritisak biti isti u dvije tačke koje leže na različitim nivoima u postavljenoj koso suženoj cijevi kroz koju teče idealan fluid?

2. Zašto se mlaz tekućine koji izlazi iz rupe sve više i više kompresuje kako se udaljava od rupe?

3. Kako su faze oscilacija ubrzanja i pomaka povezane sa harmonijskim oscilacijama?

Stanje kretanja fluida se može odrediti specificiranjem za svaku tačku u prostoru vektor brzine kao funkciju vremena.

Skup vektora specificiranih za sve tačke u prostoru formira polje vektora brzine, koje se može prikazati na sljedeći način. Nacrtajmo linije u fluidu koji se kreće tako da se tangenta na njih u svakoj tački poklapa u pravcu sa vektorom (slika 7.1). Ove linije se nazivaju strujne linije. Dogovorimo se da crtamo strujne linije tako da njihova gustina (omjer broja linija i veličine površine okomite na njih, kroz koju prolaze) bude proporcionalna veličini brzine na datom mjestu. Tada će, prema obrascu strujnih linija, biti moguće procijeniti ne samo smjer, već i veličinu vektora u različitim točkama u prostoru: gdje je brzina veća, strujne linije će biti gušće.

Broj strujnih linija koje prolaze kroz mjesto okomito na strujne linije je jednak, ako je mjesto proizvoljno orijentirano na strujne linije, broj strujnih linija je, gdje je ugao između smjera vektora i normale na mjesto. Često se koristi notacija. Broj strujnih linija kroz područje konačnih dimenzija određen je integralom:. Integral ove vrste naziva se vektorski tok kroz platformu.

Veličina i smjer vektora se mijenjaju s vremenom, stoga uzorak linija ne ostaje konstantan. Ako u svakoj tački u prostoru vektor brzine ostaje konstantan po veličini i smjeru, tada se tok naziva stacionarnim ili stacionarnim. U stacionarnom toku, bilo koja čestica tečnosti prolazi kroz datu tačku u prostoru istom brzinom. Obrazac strujne linije u ovom slučaju se ne mijenja, a strujne linije se poklapaju s putanjama čestica.

Razmotrimo polje vektora brzine nestišljivog kontinuiranog fluida. Protok vektora brzine kroz određenu površinu jednak je volumenu tekućine koja teče kroz ovu površinu u jedinici vremena. Konstruirajmo zamišljenu zatvorenu površinu S u blizini tačke P (slika 7.2). Ako u volumenu V, ograničenom površinom, tekućina ne nastaje i ne nestaje, tada će protok prema van kroz površinu biti jednak nuli. Razlika protoka od nule će ukazati da unutar površine postoje izvori ili ponori tečnosti, odnosno tačke u kojima tečnost ulazi u zapreminu (izvori) ili se uklanja iz zapremine (ponori). Brzina protoka određuje ukupnu snagu izvora i sudopere. Uz prevlast izvora nad efluentima, protok je pozitivan, sa prevlašću efluenta - negativan.

Kvocijent dijeljenja protoka sa zapreminom iz koje protiče izlazi je prosječna specifična snaga izvora zatvorenih u zapremini V. Što je manji volumen V, koji uključuje tačku P, to je ova prosječna vrijednost bliža pravoj specifičnoj snazi pri ovu tačku. U limitu na, tj. kada sažimamo zapreminu u tačku, dobijamo pravu specifičnu snagu izvora u tački P, nazvanu divergencija (divergencija) vektora:. Rezultirajući izraz vrijedi za bilo koji vektor. Integracija se vrši preko zatvorene površine S, graničnog volumena V. Divergencija je određena ponašanjem vektorske funkcije blizu tačke P. Divergencija je skalarna funkcija koordinata koje određuju položaj tačke P u prostoru.

Nađimo izraz za divergenciju u Dekartovom koordinatnom sistemu. Razmotrimo u blizini tačke P (x, y, z) mali volumen u obliku paralelepipeda sa ivicama paralelnim sa koordinatnim osama (slika 7.3). S obzirom na malenost volumena (težićemo na nulu), vrijednosti unutar svake od šest lica paralelepipeda mogu se smatrati nepromijenjenim. Protok preko cijele zatvorene površine formira se od tokova koji teku kroz svaku od šest strana posebno.

Nađimo protok kroz par lica okomitih na graničnik X na slici 7.3 lica 1 i 2). Vanjska normala na lice 2 poklapa se sa smjerom ose X. Dakle, protok kroz lice 2 je jednak. Normal ima smjer suprotan od osi X. Projekcije vektora na os X i na normalu imaju suprotne predznake, a protok kroz lice 1 je. Ukupan protok u smjeru X je. Razlika je prirast kada se pomakne duž X-ose za. Zbog svoje male veličine, ovaj prirast se može predstaviti u obliku. Onda dobijamo. Slično, kroz parove lica okomitih na Y i Z ose, tokovi su jednaki i. Potpuni protok kroz zatvorenu površinu. Podijeleći ovaj izraz sa, nalazimo divergenciju vektora u tački P:

Poznavajući divergenciju vektora u svakoj tački u prostoru, moguće je izračunati tok ovog vektora kroz bilo koju površinu konačnih dimenzija. Da bismo to učinili, dijelimo volumen ograničen površinom S na beskonačno veliki broj infinitezimalnih elemenata (slika 7.4).

Za bilo koji element, tok vektora kroz površinu tog elementa je. Zbrajanjem svih elemenata dobijamo protok kroz površinu S, ograničavajući zapreminu V:, integracija se vrši na zapreminu V, ili

Ovo je Ostrogradsky-Gaussova teorema. Ovdje je vektor jedinične normale na površinu dS u datoj tački.

Vratimo se na tok nestišljivog fluida. Nacrtajmo konturu. Zamislite da smo nekako trenutno zamrznuli tečnost u cijelom volumenu, s izuzetkom vrlo tankog zatvorenog kanala konstantnog poprečnog presjeka, koji uključuje konturu (slika 7.5). U zavisnosti od prirode toka, tečnost u formiranom kanalu će biti ili stacionarna ili će se kretati (kružiti) duž konture u jednom od mogućih smerova. Kao mjera ovog kretanja, odabrana je vrijednost jednaka proizvodu brzine fluida u kanalu i dužine kruga. Ova vrijednost se naziva cirkulacija vektora duž konture (pošto kanal ima konstantan poprečni presjek i modul brzine se ne mijenja). U trenutku stvrdnjavanja zidova, za svaku česticu tekućine u kanalu, komponenta brzine okomita na zid će se ugasiti, a ostat će samo komponenta tangentna na konturu. Ova komponenta je povezana sa impulsom, čiji je modul za česticu tečnosti zatvorenu u kanal dužine jednak, gde je gustina tečnosti, je presek kanala. Tečnost je idealna - nema trenja, tako da djelovanje zidova može promijeniti samo smjer, njegova vrijednost će ostati konstantna. Interakcija između čestica tekućine će uzrokovati takvu preraspodjelu količine gibanja između njih, koja će izjednačiti brzine svih čestica. U ovom slučaju je sačuvan algebarski zbir impulsa, dakle gdje je brzina cirkulacije, tangencijalna komponenta brzine fluida u zapremini u trenutku koji prethodi stvrdnjavanju zidova. Dijelimo sa, dobijamo.

Cirkulacija karakteriše svojstva polja, usrednjena za oblast sa dimenzijama reda prečnika konture. Da bi se dobila karakteristika polja u tački P, potrebno je smanjiti veličinu konture, skupljajući je do tačke P. U ovom slučaju, granica omjera vektorske cirkulacije duž ravne konture koja se skuplja do tačke P do veličina ravni konture S uzima se kao karakteristika polja:. Vrijednost ove granice ne zavisi samo od svojstava polja u tački P, već i od orijentacije konture u prostoru, koja se može specificirati smjerom pozitivne normale na ravan konture (pridružena normala sa smjerom pomicanja konture po pravilu desnog zavrtnja smatra se pozitivnim). Određivanjem ove granice za različite smjerove dobijamo različite vrijednosti, a za suprotne normalne smjerove ove vrijednosti se razlikuju po predznaku. Za određeni smjer normale, vrijednost granice će biti maksimalna. Dakle, vrijednost granice se ponaša kao projekcija nekog vektora na smjer normale na ravan konture duž koje se odvija cirkulacija. Maksimalna vrijednost granice određuje modul ovog vektora, a smjer pozitivne normale na kojoj se postiže maksimum daje smjer vektora. Ovaj vektor se naziva rotor ili vrtlog vektora:.

Da bi se pronašla projekcija rotora na os kartezijanskog koordinatnog sistema, potrebno je odrediti granične vrijednosti za takve orijentacije mjesta S, pri čemu se normala na mjesto poklapa s jednom od osa X, Y, Z . Ako, na primjer, usmjeriti duž X-ose, naći ćemo. Kontura se u ovom slučaju nalazi u ravnini paralelnoj sa YZ, uzimamo konturu u obliku pravokutnika sa stranicama i. Kod vrijednosti i na svakoj od četiri strane, kontura se može smatrati nepromijenjenom. Odsjek 1 konture (slika 7.6) je suprotan osi Z, stoga se u ovom dijelu poklapa sa, u presjeku 2, u presjeku 3, u presjeku 4. Za cirkulaciju duž ovog kola dobijamo vrijednost:. Razlika je u inkrementu kada se pomakne duž Y za. Zbog svoje male veličine, ovaj prirast se može predstaviti u obliku.Slično, razlika. Zatim cirkulacija duž razmatrane konture,

gdje je površina konture. Dijelimo cirkulaciju sa, nalazimo projekciju rotora na X-osu:. Slično,,. Tada je rotor vektora određen izrazom: +,

Poznavajući rotor vektora u svakoj tački neke površine S, možemo izračunati cirkulaciju ovog vektora duž konture koja ograničava površinu S. Da bismo to učinili, podijelimo površinu na vrlo male elemente (slika 7.7). Cirkulacija duž granične konture je, gdje je pozitivna normala na element. Sumirajući ove izraze preko cijele površine S i zamjenom izraza za cirkulaciju, dobivamo. Ovo je Stokesova teorema.

Dio fluida omeđen strujnim linijama naziva se strujna cijev. Vektor, koji je u svakoj tački tangentan na strujnu liniju, bit će tangentan na površinu potočne cijevi, a čestice fluida ne prelaze zidove potočne cijevi.

Razmotrimo poprečni presjek strujne cijevi S (slika 7.8.), okomito na smjer brzine. Pretpostavićemo da je brzina čestica tečnosti ista u svim tačkama ovog odseka. Vremenom će sve čestice čija udaljenost u početnom trenutku ne prelazi vrijednost proći će kroz poprečni presjek S. Prema tome, zapremina tečnosti jednaka će proći kroz deo S u vremenu, a zapremina tečnosti jednaka će proći kroz deo S u jedinici vremena Pretpostavljamo da je strujna cev toliko tanka da je brzina čestica u svakoj njegovih sekcija može se smatrati konstantnim. Ako je fluid nestišljiv (tj. njegova gustina je svuda ista i ne mijenja se), tada će količina fluida između sekcija i (slika 7.9.) ostati nepromijenjena. Tada količine tekućine koje teče u jedinici vremena kroz sekcije i moraju biti iste:

Dakle, za nestišljiv fluid, vrijednost u bilo kojem dijelu iste protočne cijevi mora biti ista:

Ova izjava se zove teorema o kontinuitetu mlaza.

Kretanje idealnog fluida opisuje se Navier-Stokesovom jednačinom:

gdje je t vrijeme, x, y, z koordinate čestice tečnosti, projekcije zapreminske sile, p je pritisak, a ρ je gustina medija. Ova jednadžba vam omogućava da odredite projekciju brzine čestice medija kao funkciju koordinata i vremena. Da bi se sistem zatvorio, jednačina kontinuiteta se dodaje Navier-Stokesovoj jednačini, koja je posljedica teoreme o kontinuitetu mlaza:

Za integraciju ovih jednačina potrebno je postaviti početne (ako kretanje nije stacionarno) i granične uslove.

7.2. Pritisak u tekućini koja teče. Bernulijeva jednačina i njene posljedice

S obzirom na kretanje fluida, u nekim slučajevima se može pretpostaviti da kretanje nekih fluida u odnosu na druge nije povezano sa pojavom sila trenja. Tečnost bez unutrašnjeg trenja (viskoziteta) naziva se idealnom.

Odaberimo protočnu cijev malog presjeka u idealnom fluidu koji miruje teče (slika 7.10). Razmotrimo zapreminu tečnosti omeđenu zidovima potočne cevi i presecima i okomito na strujne linije.Za vreme ovog volumena će se kretati duž potočne cevi, a deonica će se pomeriti u poziciju nakon što prođe put, sekcija će se pomjeriti na poziciju nakon prolaska putanje. Zbog kontinuiteta mlaza, osenčeni volumeni će imati istu vrijednost:

Energija svake čestice tečnosti jednaka je zbiru njene kinetičke energije i potencijala u polju gravitacije. Zbog stacionarnosti toka, čestica koja se nalazi nakon nekog vremena u bilo kojoj od tačaka nezasjenjenog dijela zapremine koja se razmatra (na primjer, tačka O na slici 7.10) ima istu brzinu (i istu kinetičku energiju) kao čestica koja se nalazila u istoj tački u početnom trenutku. Stoga je povećanje energije cjelokupnog volumena koji se razmatra jednak razlici u energijama zasjenjenih volumena i.

U idealnom fluidu ne postoje sile trenja, pa je prirast energije (7.1) jednak radu sila pritiska na dodeljenoj zapremini. Sile pritiska na bočnu površinu su okomite u svakoj tački na smjer kretanja čestica i ne vrše rad. Rad sila primijenjenih na presjeke jednak je

Izjednačavanjem (7.1) i (7.2) dobijamo

Pošto su presjeci i uzeti proizvoljno, može se tvrditi da izraz ostaje konstantan u bilo kojem dijelu strujne cijevi, tj. u stacionarnom toku idealnom fluidu duž bilo koje strujne linije, uslov

Ovo je Bernoullijeva jednačina. Za horizontalnu strujnu liniju, jednačina (7.3) ima oblik:

7.3 ISPUŠTANJE TEČNOSTI IZ VENTILACA

Primijenimo Bernoullijevu jednačinu na slučaj istjecanja tekućine iz male rupe u širokoj otvorenoj posudi. Odaberimo protočnu cijev u tekućini, čiji gornji dio leži na površini tekućine, a donji se poklapa sa rupom (slika 7.11). U svakoj od ovih dionica brzina i visina iznad određenog početnog nivoa mogu se smatrati istim, pritisci u oba odsjeka su jednaki atmosferskim i također isti, brzina kretanja otvorene površine će se smatrati jednakom nuli. Tada jednačina (7.3) poprima oblik:

Puls

7.4 Viskozna tečnost. Sile unutrašnjeg trenja

Idealna tečnost, tj. fluid bez trenja je apstrakcija. Sve stvarne tečnosti i gasovi imaju veći ili manji viskozitet ili unutrašnje trenje.

Viskoznost se očituje u tome što se kretanje koje je nastalo u tekućini ili plinu, nakon prestanka djelovanja sila koje su ga izazvale, postepeno zaustavlja.

Razmotrimo dvije paralelne ploče postavljene u tekućinu (slika 7.12). Linearne dimenzije ploča su mnogo veće od udaljenosti između njih. d... Donja ploča se drži na mjestu, gornja ploča se s nekim pomjera u odnosu na donju

brzina. Eksperimentalno je dokazano da je za pomicanje gornje ploče konstantnom brzinom potrebno djelovati na nju sasvim određenom silom konstantne veličine. Ploča ne prima ubrzanje, stoga je djelovanje ove sile uravnoteženo silom koja joj je jednaka po veličini, a to je sila trenja koja djeluje na ploču kada se kreće u tekućini. Označimo to, a dio tečnosti koji leži ispod ravni deluje silom na deo tečnosti koji leži iznad ravni. Štaviše, i određene su formulom (7.4). Dakle, ova formula izražava silu između dodirnih slojeva fluida.

Eksperimentalno je dokazano da se brzina čestica tekućine mijenja u smjeru z, okomito na ploče (slika 7.6) prema linearnom zakonu

Čini se da se čestice tekućine u direktnom kontaktu s pločama lijepe za njih i imaju istu brzinu kao i same ploče. Iz formule (7.5) dobijamo

Predznak modula u ovoj formuli je postavljen iz sljedećeg razloga. Kada se promijeni smjer kretanja, derivacija brzine mijenja predznak, dok je omjer uvijek pozitivan. S obzirom na gore navedeno, izraz (7.4) poprima oblik

Jedinica za viskozitet sa SI je viskoznost pri kojoj gradijent brzine sa modulom dovodi do pojave sile unutrašnjeg trenja od 1 N po 1m kontaktne površine slojeva. Ova jedinica se zove Pascal - sekunda (Pa · s).

1 | | | |

Pregledi