Ecuații de grade superioare. Ecuații de putere sau exponențiale Ecuație de gradul 5

Clasă: 9

Obiective de bază:

1. Pentru a consolida conceptul de ecuație rațională întreagă de gradul al treilea.
2. Formulați principalele metode de rezolvare a ecuațiilor de grade superioare (n > 3).
3. Să predea metodele de bază pentru rezolvarea ecuațiilor de grade superioare.
4. Să învețe prin forma ecuației să determine cel mai eficient mod de a o rezolva.

Forme, metode și tehnici pedagogice care sunt folosite de profesor în clasă:

• Sistem de instruire curs-seminar (prelegeri - explicarea noului material, seminarii - rezolvarea problemelor).
• Tehnologii informaționale și comunicaționale (sondaj frontal, lucru oral cu clasa).
• Formare diferențiată, forme de grup și individuale.
• Utilizarea metodei cercetării în predare, care vizează dezvoltarea aparatului matematic și a abilităților mentale ale fiecărui elev în parte.
• Material tipărit - un rezumat individual al lecției (concepte de bază, formule, enunțuri, materialul de curs este comprimat sub formă de diagrame sau tabele).

Planul lecției:

1. Organizarea timpului.
   Scopul etapei: includerea elevilor în activitățile de învățare, determinarea conținutului lecției.
2. Actualizarea cunoștințelor elevilor.
   Scopul etapei: actualizarea cunoștințelor elevilor pe teme conexe studiate anterior
3. Învățarea unui subiect nou (prelecție). Scopul etapei: formularea principalelor metode de rezolvare a ecuațiilor de grade superioare (n > 3)
4. Rezumând.
   Scopul etapei: evidențierea din nou a punctelor cheie din materialul studiat în lecție.
5. Teme pentru acasă.
   Scopul etapei: formularea temelor pentru elevi.

Rezumatul lecției

1. Moment organizatoric.

Formularea temei lecției: „Ecuații de grade superioare. Metode de rezolvare a acestora”.

2. Actualizarea cunoștințelor elevilor.

Sondaj teoretic – conversație. Repetarea unor informații studiate anterior din teorie. Elevii formulează definiții de bază și dau enunțuri ale teoremelor necesare. Sunt date exemple care demonstrează nivelul de cunoștințe dobândite anterior.

• Conceptul de ecuație cu o variabilă.
• Conceptul de rădăcină a ecuației, soluția ecuației.
• Conceptul de ecuație liniară cu o variabilă, conceptul de ecuație pătratică cu o variabilă.
• Conceptul de echivalență a ecuațiilor, ecuație-consecințe (conceptul de rădăcini străine), tranziție nu prin consecință (cazul pierderii rădăcinilor).
• Conceptul unei întregi expresii raționale cu o variabilă.
• Conceptul unei întregi ecuații raționale n gradul. Forma standard a unei întregi ecuații raționale. Întreaga ecuație rațională redusă.
• Trecerea la un set de ecuații de grade inferioare prin factorizarea ecuației inițiale.
• Conceptul de polinom n gradul de la X. teorema lui Bezout. Consecințele teoremei lui Bezout. teoreme rădăcinilor ( Z-rădăcini și Q-rădăcini) a unei întregi ecuații raționale cu coeficienți întregi (reduși și respectiv nereduși).
• Schema lui Horner.

3. Învățarea unui subiect nou.

Vom lua în considerare întreaga ecuație rațională n puterea formei standard cu o variabilă necunoscută x:Pn(x)= 0, unde P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0– polinom n gradul de la X, A n ≠ 0 . Dacă A n = 1 atunci o astfel de ecuație se numește ecuație rațională întreagă redusă n gradul. Să luăm în considerare astfel de ecuații pentru diferite valori nși enumerați principalele metode de soluționare a acestora.

n= 1 este o ecuație liniară.

n= 2 este o ecuație pătratică. Formula discriminantă. Formula pentru calcularea rădăcinilor. teorema lui Vieta. Selectarea unui pătrat complet.

n= 3 este o ecuație cubică.

metoda de grupare.

Exemplu: x 3 – 4x 2 – x+ 4 = 0 (x - 4) (x 2– 1) = 0 X 1 = 4 , x2 = 1,X 3 = -1.

Ecuația cubică reciprocă a formei topor 3 + bx 2 + bx + A= 0. Rezolvăm combinând termeni cu aceiași coeficienți.

Exemplu: X 3 – 5X 2 – 5X + 1 = 0 (X + 1)(X 2 – 6X + 1) = 0 X 1 = -1, X 2 = 3 + 2, X 3 = 3 – 2.

Selectarea rădăcinilor Z pe baza teoremei. Schema lui Horner. La aplicarea acestei metode, este necesar să subliniem că enumerarea în acest caz este finită și selectăm rădăcinile după un anumit algoritm în conformitate cu teorema de pe Z-rădăcinile ecuației raționale întregi reduse cu coeficienți întregi.

Exemplu: X 3 – 9X 2 + 23X– 15 = 0. Ecuația se reduce. Scriem divizorii termenului liber ( + 1; + 3; + 5; + 15). Să aplicăm schema lui Horner:

	X 3	X 2	X 1	X 0	concluzie
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - rădăcină
	X 2	X 1	X 0

Primim ( X – 1)(X 2 – 8X + 15) = 0 X 1 = 1, X 2 = 3, X 3 = 5.

Ecuație cu coeficienți întregi. Selectarea rădăcinilor Q pe baza teoremei. Schema lui Horner. La aplicarea acestei metode, este necesar să subliniem că enumerarea în acest caz este finită și selectăm rădăcinile după un anumit algoritm în conformitate cu teorema de pe Q-rădăcinile unei ecuații raționale întregi nereduse cu coeficienți întregi.

Exemplu: 9 X 3 + 27X 2 – X– 3 = 0. Ecuația nu este redusă. Scriem divizorii termenului liber ( + 1; + 3). Să scriem divizorii coeficientului la cea mai mare putere a necunoscutului. ( + 1; + 3; + 9) Prin urmare, vom căuta rădăcini printre valori ( + 1; + ; + ; + 3). Să aplicăm schema lui Horner:

	X 3	X 2	X 1	X 0	concluzie
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 nu este o rădăcină
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 nu este o rădăcină
	9	x9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	rădăcină
	X 2	X 1	X 0

Primim ( X – )(9X 2 + 30X + 9) = 0 X 1 = , X 2 = - , X 3 = -3.

Pentru confortul calculului atunci când alegeți Q -rădăcini poate fi convenabil să faceți o schimbare a variabilei, mergeți la ecuația de mai sus și ajustați Z -rădăcini.

• Dacă interceptarea este 1

.

• Dacă este posibil să se folosească înlocuirea formularului y=kx

.

Formula Cardano. Există o metodă universală pentru rezolvarea ecuațiilor cubice - aceasta este formula Cardano. Această formulă este asociată cu numele matematicienilor italieni Gerolamo Cardano (1501–1576), Nicolo Tartaglia (1500–1557), Scipio del Ferro (1465–1526). Această formulă se află în afara domeniului de aplicare al cursului nostru.

n= 4 este o ecuație de gradul al patrulea.

metoda de grupare.

Exemplu: X 4 + 2X 3 + 5X 2 + 4X – 12 = 0 (X 4 + 2X 3) + (5X 2 + 10X) – (6X + 12) = 0 (X + 2)(X 3 + 5X- 6) = 0 (X + 2)(X– 1)(X 2 + X + 6) = 0 X 1 = -2, X 2 = 1.

Metoda de înlocuire variabilă.

• Ecuația biquadratică a formei topor 4 + bx 2+s = 0 .

Exemplu: X 4 + 5X 2 - 36 = 0. Înlocuire y = X 2. De aici y 1 = 4, y 2 = -9. Asa de X 1,2 = + 2 .

• Ecuația reciprocă a gradului al patrulea al formei topor 4 + bx 3+c X 2 + bx + A = 0.

Rezolvăm combinând termeni cu aceiași coeficienți prin înlocuirea formei

• topor 4 + bx 3 + cx 2 – bx + A = 0.

• Ecuație inversă generalizată a gradului al patrulea al formei topor 4 + bx 3 + cx 2 + kbx + k2 a = 0.

• Înlocuire generală. Câteva înlocuiri standard.

Exemplul 3 . Înlocuirea vederii generale(decurge din forma unei anumite ecuații).

n = 3.

Ecuație cu coeficienți întregi. Selectarea rădăcinilor Q n = 3.

Formula generala. Există o metodă universală de rezolvare a ecuațiilor de gradul al patrulea. Această formulă este asociată cu numele lui Ludovico Ferrari (1522-1565). Această formulă se află în afara domeniului de aplicare al cursului nostru.

n > 5 - ecuații ale gradului cinci și superior.

Ecuație cu coeficienți întregi. Selectarea rădăcinilor Z pe baza teoremei. Schema lui Horner. Algoritmul este similar cu cel discutat mai sus pentru n = 3.

Ecuație cu coeficienți întregi. Selectarea rădăcinilor Q pe baza teoremei. Schema lui Horner. Algoritmul este similar cu cel discutat mai sus pentru n = 3.

Ecuații simetrice. Orice ecuație reciprocă de grad impar are rădăcină X= -1 și după descompunerea lui în factori, obținem că un factor are forma ( X+ 1), iar al doilea factor este o ecuație reciprocă de grad par (gradul său este cu unul mai mic decât gradul ecuației inițiale). Orice ecuație reciprocă de grad par împreună cu o rădăcină a formei x = φ conţine şi rădăcina formei . Folosind aceste afirmații, rezolvăm problema scăzând gradul ecuației studiate.

Metoda de înlocuire variabilă. Utilizarea omogenității.

Nu există o formulă generală pentru rezolvarea ecuațiilor întregi de gradul cinci (acest lucru a fost arătat de matematicianul italian Paolo Ruffini (1765–1822) și de matematicianul norvegian Nils Henrik Abel (1802–1829)) și puteri superioare (așa a fost demonstrat de francezii). matematicianul Evariste Galois (1811–1832) )).

• Amintiți-vă din nou că în practică este posibil să se utilizeze combinatii metodele enumerate mai sus. Este convenabil să treceți la un set de ecuații de grade inferioare prin factorizarea ecuației inițiale.
• În afara sferei de aplicare a discuției noastre de astăzi, sunt utilizate pe scară largă în practică metode grafice rezolvarea ecuaţiilor şi metode de rezolvare aproximativă ecuații de grade superioare.
• Există situații în care ecuația nu are rădăcini R.
Apoi soluția se reduce la a arăta că ecuația nu are rădăcini. Pentru a demonstra acest lucru, analizăm comportamentul funcțiilor considerate pe intervale de monotonitate. Exemplu: ecuație X 8 – X 3 + 1 = 0 nu are rădăcini.
• Folosind proprietatea de monotonitate a funcțiilor
. Există situații în care utilizarea diferitelor proprietăți ale funcțiilor ne permite să simplificăm sarcina.
Exemplul 1: Ecuația X 5 + 3X– 4 = 0 are o rădăcină X= 1. Prin proprietatea de monotonitate a funcţiilor analizate nu există alte rădăcini.
Exemplul 2: Ecuația X 4 + (X– 1) 4 = 97 are rădăcini X 1 = -2 și X 2 = 3. Analizând comportamentul funcțiilor corespunzătoare pe intervalele de monotonitate, concluzionăm că nu există alte rădăcini.

4. Rezumând.

Rezumat: Acum am stăpânit metodele de bază pentru rezolvarea diferitelor ecuații de grade superioare (pentru n > 3). Sarcina noastră este să învățăm cum să folosim eficient algoritmii de mai sus. În funcție de tipul de ecuație, va trebui să învățăm cum să stabilim care metodă de soluție este cea mai eficientă în acest caz, precum și să aplicăm corect metoda aleasă.

5. Tema pentru acasă.

: poz. 7, p. 164–174, nr. 33–36, 39–44, 46,47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Posibile subiecte ale rapoartelor sau rezumatelor pe această temă:

• Formula Cardano
• Metoda grafica de rezolvare a ecuatiilor. Exemple de soluții.
• Metode de rezolvare aproximativă a ecuațiilor.

Analiza asimilării materialului și a interesului studenților pentru temă:

Experiența arată că interesul elevilor este în primul rând posibilitatea de a selecta Z-rădăcini și Q-rădăcinile ecuațiilor folosind un algoritm destul de simplu folosind schema lui Horner. Elevii sunt, de asemenea, interesați de diferite tipuri standard de substituție de variabile, care pot simplifica semnificativ tipul de problemă. Metodele grafice de rezolvare sunt de obicei de interes deosebit. În acest caz, puteți analiza în plus sarcinile într-o metodă grafică pentru rezolvarea ecuațiilor; discutați vederea generală a graficului pentru un polinom de 3, 4, 5 grade; analizați modul în care numărul de rădăcini ale ecuațiilor de 3, 4, 5 grade este legat de tipul graficului corespunzător. Mai jos este o listă de cărți în care puteți găsi informații suplimentare despre acest subiect.

Bibliografie:

1. Vilenkin N.Ya. etc „Algebră. Un manual pentru elevii din clasele a IX-a cu un studiu aprofundat al matematicii ”- M., Educație, 2007 - 367 p.
2. Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.„În spatele paginilor unui manual de matematică. Aritmetic. Algebră. Clasele 10-11” – M., Iluminismul, 2008 – 192 p.
3. Vygodsky M.Ya.„Manual de matematică” - M., AST, 2010 - 1055 p.
4. Galitsky M.L.„Colecție de probleme în algebră. Manual pentru clasele 8-9 cu studiu aprofundat de matematică ”- M., Educație, 2008 - 301 p.
5. Zvovich L.I. et al. „Algebra și începuturile analizei. 8-11 celule Un manual pentru școli și clase cu studiu aprofundat al matematicii ”- M., Drofa, 1999 - 352 p.
6. Zvavich L.I., Averianov D.I., Pigarev B.P., Trushanina T.N.„Teme de matematică pentru pregătirea unui examen scris în clasa a 9-a” - M., Educație, 2007 - 112 p.
7. Ivanov A.A., Ivanov A.P.„Probe tematice pentru sistematizarea cunoștințelor în matematică” partea 1 - M., Fizmatkniga, 2006 - 176 p.
8. Ivanov A.A., Ivanov A.P.„Probe tematice pentru sistematizarea cunoștințelor în matematică” partea 2 - M., Fizmatkniga, 2006 - 176 p.
9. Ivanov A.P.„Teste și teste la matematică. Tutorial". - M., Fizmatkniga, 2008 - 304 p.
10. Leibson K.L.„Culegere de sarcini practice la matematică. Clasa Part 2–9” – M., MTsNMO, 2009 – 184 p.
11. Makarychev Yu.N., Mindyuk N.G."Algebră. Capitole suplimentare pentru manualul școlii de clasa a IX-a. Manual pentru elevii școlilor și claselor cu studiu aprofundat al matematicii.” - M., Educație, 2006 - 224 p.
12. Mordkovich A.G."Algebră. Studiu aprofundat. clasa a 8-a. Manual” – M., Mnemosyne, 2006 – 296 p.
13. Savin A.P.„Dicționar enciclopedic al unui tânăr matematician” - M., Pedagogie, 1985 - 352 p.
14. Survillo G.S., Simonov A.S.„Materiale didactice de algebră pentru clasa a IX-a cu studiu aprofundat al matematicii” - M., Educație, 2006 - 95 p.
15. Chulkov P.V.„Ecuații și inegalități în cursul școlar de matematică. Prelegeri 1–4” – M., I septembrie 2006 – 88 p.
16. Chulkov P.V.„Ecuații și inegalități în cursul școlar de matematică. Prelegeri 5–8” – M., 1 septembrie 2009 – 84 p.

În secolul al XVI-lea, matematicienii au dat peste numere complexe aproape întâmplător (vezi capitolul 11). Până în secolul al XVIII-lea, numerele complexe au fost considerate o extensie a numerelor reale, dar lucrul cu ele încă a condus la o eroare de paritate, așa cum în Leonard E, marea sa lucrare despre teoria numerelor, Investigații aritmetice (1801), a evitat utilizarea astfel. -numite „numere imaginare”. Mi se pare că cea mai importantă parte a acestei lucrări este prima demonstrație a teoremei fundamentale a algebrei. Gauss și-a dat seama cât de importantă era această teoremă, creând câteva dovezi suplimentare în anii următori. În 1849 a revizuit prima versiune, de data aceasta folosind numere complexe. Folosind termeni moderni, putem spune că pentru orice ecuație polinomială finită cu coeficienți reali sau complexi, toate rădăcinile sale vor fi numere reale sau complexe. Astfel, obținem un răspuns negativ la vechea întrebare dacă soluția ecuațiilor polinomiale de ordin înalt necesită crearea unor numere de ordin mai mare decât a celor complexe.

Una dintre cele mai spinoase probleme din algebra de atunci a fost întrebarea dacă putem rezolva prin metode algebrice, adică folosind un număr finit de pași algebrici, un polinom de ordinul cinci - o chintică. Acum, școala învață formula pentru rezolvarea ecuațiilor pătratice, iar din secolul al XVI-lea, metode similare sunt cunoscute pentru rezolvarea ecuațiilor de gradul al treilea și al patrulea (Capitolul 11). Dar nu a fost găsită nicio metodă pentru chintice. Poate părea că teorema fundamentală a algebrei conține promisiunea unui răspuns pozitiv, dar de fapt garantează pur și simplu că există soluții, nu spune nimic despre existența unor formule care dau soluții exacte (metode numerice și grafice aproximative existau deja de către acel timp). Și apoi au fost două genii matematice cu o soartă tragică.

Niels Henrik Abel (1802–1829) s-a născut într-o familie numeroasă și săracă care trăiește într-un mic sat din Norvegia, o țară devastată de ani lungi de război cu Anglia și Suedia. Profesorul, care era prietenos cu băiatul, îi dădea lecții particulare, dar după moartea tatălui său, la vârsta de optsprezece ani, în ciuda vârstei sale fragede și a sănătății fragile, Abel a fost nevoit să-și întrețină familia. În 1824, a publicat un articol științific în care afirma că quintica nu este rezolvabilă algebric, ca, într-adevăr, orice polinom de ordin superior. Abel credea că acest articol îi va servi drept trecere în lumea științifică și l-a trimis lui Gauss de la Universitatea din Göttingen. Din păcate, Gauss nu a apucat niciodată să taie paginile cu un cuțit (orice cititor trebuia să facă asta în acele zile) și nu a citit articolul. În 1826, guvernul norvegian a oferit în sfârșit fonduri pentru ca Abel să călătorească prin Europa. De teamă că contactul personal cu Gauss nu i-ar aduce o mare bucurie, matematicianul a decis să nu viziteze Göttingen și a plecat în schimb la Berlin. Acolo s-a împrietenit cu August Leopold Crelle (1780–1855), un matematician, arhitect și inginer care a consiliat Ministerul Prusac al Educației în materie de matematică. Krell urma să înființeze Journal of Pure and Applied Mathematics. Așa că Abel a avut ocazia să-și distribuie lucrările și să publice multe, mai ales în primele numere ale Revistei, care a început imediat să fie considerată o publicație științifică foarte prestigioasă și cu autoritate. Norvegianul a publicat acolo o versiune extinsă a dovezii sale că quintica este de nerezolvat prin metode algebrice. Și apoi a plecat la Paris. Această călătorie l-a supărat foarte tare pe Abel, pentru că practic nu a primit sprijinul matematicienilor francezi de care avea atâta nevoie. El a devenit apropiat de Augustin Louis Cauchy (1789–1857), care la acea vreme era lumina principală a analizei matematice, dar de natură foarte complexă. După cum a spus însuși Abel, „Cauchy este nebun și nu se poate face nimic în privința asta, deși în prezent el este singurul capabil de orice în matematică”. Dacă cineva încearcă să justifice lipsa de respect și disprețul care emană de la Gauss și Cauchy, se poate spune că Quintic a atins o anumită faimă și a atras atenția atât a matematicienilor respectați, cât și a originalilor. Abel s-a întors în Norvegia, unde suferea din ce în ce mai mult de tuberculoză. El a continuat să-și trimită lucrările la Crelle, dar a murit în 1829, neștiind în ce măsură reputația sa crescuse în lumea științifică. La două zile după moartea sa, Abel a primit o ofertă de a ocupa un post științific la Berlin.

Abel a arătat că orice polinom de peste ordinul al patrulea nu poate fi rezolvat folosind radicali, cum ar fi rădăcinile pătrate, rădăcinile cubice sau de ordin superior. Cu toate acestea, condițiile explicite în care, în cazuri speciale, aceste polinoame puteau fi rezolvate, precum și metoda de rezolvare a acestora, au fost formulate de Galois. Évariste Galois (1811–1832) a trăit o viață scurtă și plină de evenimente. Era un matematician incredibil de talentat. Galois a fost necruțător față de cei pe care îi considera mai puțin talentați decât el și, în același timp, nu putea suporta nedreptatea socială. Nu a arătat nicio aptitudine pentru matematică până când a citit Elementele de geometrie a lui Legendre (publicată în 1794, această carte a fost principalul manual pentru următoarele sute de ani). Apoi a înghițit literalmente restul lucrărilor lui Legendre și, mai târziu, Abel. Entuziasmul, încrederea în sine și intoleranța lui au dus la consecințe cu adevărat îngrozitoare în relațiile sale cu profesorii și examinatorii. Galois a participat la concursul de admitere la Școala Politehnică - leagănul matematicii franceze, dar din cauza nepregătirii a picat examenul. De ceva vreme după ce a întâlnit un nou profesor care i-a recunoscut talentul, a reușit să-și țină temperamentul sub control. În martie 1829, Galois a publicat prima sa lucrare despre fracțiile continue, pe care o considera cea mai semnificativă lucrare. A trimis un mesaj despre descoperirile sale Academiei de Științe, iar Cauchy a promis că le va prezenta, dar a uitat. Mai mult, pur și simplu a pierdut manuscrisul.

Al doilea eșec al lui Galois de a intra la Școala Politehnică a intrat în folclorul matematic. Era atât de obișnuit să aibă în mod constant idei matematice complexe în cap, încât a fost înfuriat de mișcarea meschină a examinatorilor. Întrucât examinatorii au avut dificultăți în înțelegerea explicațiilor sale, el a aruncat o cârpă de ștergere în fața unuia dintre ei. La scurt timp după aceea, tatăl său a murit, sinucidendu-se ca urmare a intrigilor bisericești. O revoltă aproape că a izbucnit la înmormântarea lui. În februarie 1830, Galois a scris următoarele trei articole, trimițându-le la Academia de Științe pentru Marele Premiu la matematică. Joseph Fourier, pe atunci secretar al academiei, a murit fără să le fi citit, iar după moartea sa articolele nu s-au găsit printre lucrările sale. Un asemenea flux de dezamăgiri ar doborî pe oricine. Galois s-a răzvrătit împotriva celor de la putere pentru că a simțit că nu i-au recunoscut meritele și l-a ucis pe tatăl său. S-a cufundat cu capul în politică, devenind un republican înflăcărat - nu cea mai înțeleaptă decizie din Franța în 1830. Într-o ultimă încercare disperată, el a trimis un articol științific celebrului fizician și matematician francez Siméon Denis Poisson (1781–1840), care, în replică, a cerut dovezi suplimentare.

Acesta a fost ultimul pahar. În 1831, Galois a fost arestat de două ori - mai întâi pentru că ar fi cerut asasinarea regelui Ludovic Filip, iar apoi pentru a-l proteja - autoritățile se temeau de o revoltă republicană! De data aceasta, a fost condamnat la șase luni de închisoare sub acuzația falsă de purtare ilegală a uniformă a batalionului de artilerie desființat la care s-a alăturat. Eliberat condiționat, a început o afacere care l-a dezgustat la fel de mult ca orice altceva în viață. În scrisorile către prietenul său devotat, Chevalier, se simte dezamăgirea lui. La 29 mai 1832, a acceptat o provocare la duel, motivele pentru care nu sunt pe deplin înțelese. „Am fost victima unei cochete dezonorabile. Viața mea se estompează într-o ceartă mizerabilă”, scrie el într-o scrisoare către toți republicanii. Cea mai faimoasă lucrare a lui Galois a fost schițată cu o noapte înainte de duelul fatal. Plângerile sunt împrăștiate în margine: „Nu mai am timp, nu mai am timp”. A trebuit să lase altora detaliile etapelor intermediare care nu erau esențiale pentru înțelegerea ideii principale. Trebuia să arunce pe hârtie baza descoperirilor sale - originile a ceea ce se numește acum teorema Galois. El și-a încheiat testamentul cerându-i lui Chevalier „să le solicite lui Jacobi și Gauss să-și dea opinia public, nu asupra corectitudinii, ci asupra importanței acestor teoreme”. Dis de dimineață, Galois a mers să-și întâlnească rivalul. Au fost nevoiți să tragă de la o distanță de 25 de pași. Galois a fost rănit și a murit la spital a doua zi dimineață. Avea doar douăzeci de ani.

Galois s-a bazat pe lucrările lui Lagrange și Cauchy, dar a dezvoltat o metodă mai generală. Aceasta a fost o realizare extrem de importantă în domeniul rezolvării chinticelor. Omul de știință a acordat mai puțină atenție ecuațiilor originale sau interpretării grafice și s-a gândit mai mult la natura rădăcinilor în sine. Pentru a simplifica, Galois a considerat doar așa-numitele chintice ireductibile, adică cele care nu puteau fi factorizate sub formă de polinoame de ordin inferior (cum am spus, pentru orice ecuație polinomială de până la ordinul al patrulea există formule de găsire a rădăcinilor lor). ). În general, un polinom ireductibil cu coeficienți raționali este un polinom care nu poate fi descompus în polinoame mai simple care au coeficienți raționali. De exemplu, (x 5 - 1) poate fi factorizat (x-1)(x 4 + x 3 + x 2 + x + 1),întrucât (x 5 - 2) ireductibil. Scopul lui Galois a fost de a determina condițiile în care toate soluțiile unei ecuații polinomiale ireductibile generale pot fi găsite în termeni de radicali.

Cheia soluției este că rădăcinile oricărei ecuații algebrice ireductibile nu sunt independente, ele pot fi exprimate una în termenii celeilalte. Aceste relații au fost formalizate în grupul tuturor permutărilor posibile, așa-numitul grup de simetrie a rădăcinii - pentru o chintică acest grup conține 5! = 5 x 4 x 3 x 2 x 1 = 120 elemente. Algoritmii matematici ai teoriei Galois sunt foarte complecși și, cel mai probabil, parțial din această cauză, au fost înțeleși inițial cu mare dificultate. Dar după ce nivelul de abstractizare a făcut posibilă trecerea de la soluțiile algebrice ale ecuațiilor la structura algebrică a grupurilor asociate acestora, Galois a putut prezice solvabilitatea ecuației pe baza proprietăților unor astfel de grupuri. Mai mult, teoria sa a oferit și o metodă prin care aceste rădăcini ar putea fi găsite. În ceea ce privește chintica, matematicianul Joseph Liouville (1809–1882), care în 1846 a publicat cea mai mare parte a lucrărilor lui Galois în Journal of Pure and Applied Mathematics, a remarcat că tânărul om de știință a dovedit o „teoremă frumoasă” și pentru a „a Dacă o ecuație ireductibilă a gradului inițial este rezolvabilă în termeni de radicali, este necesar și suficient ca toate rădăcinile ei să fie funcții raționale ale oricăror două dintre ele. Deoarece acest lucru este imposibil pentru o chintică, nu poate fi rezolvat cu radicali.

În trei ani, lumea matematică a pierdut două dintre cele mai strălucitoare stele ale sale. Au urmat acuzații reciproce și cercetarea sufletească, iar Abel și Galois au obținut recunoașterea binemeritată, dar numai postum. În 1829, Carl Jacobi, prin Legendre, a aflat de manuscrisul „pierdut” al lui Abel, iar în 1830 a izbucnit un scandal diplomatic când consulul norvegian la Paris a cerut să fie găsit articolul compatriotului său. Până la urmă, Cauchy a găsit articolul, doar ca să-l piardă din nou în redactiile academiei! În același an, Abel a primit Marele Premiu la Matematică (împreună cu Jacobi) - dar era deja mort. În 1841 a fost publicată biografia lui. În 1846, Liouville a editat unele dintre manuscrisele lui Galois pentru publicare, iar în introducerea sa și-a exprimat regretul că academia a respins inițial lucrarea lui Galois din cauza complexității sale - „într-adevăr, claritatea prezentării este necesară atunci când autorul conduce cititorul în afara drumurilor bătute în teritorii sălbatice neexplorate.” El continuă: „Galois nu mai este! Să nu cădem în critici inutile. Să aruncăm defectele și să ne uităm la virtuți! Fructele scurtei vieți a lui Galois se încadrează în doar șaizeci de pagini. Editorul revistei de matematică pentru candidații la École Normale și Ecole Polytechnique a comentat cazul Galois după cum urmează: „Un candidat cu o inteligență ridicată a fost eliminat de un examinator cu un nivel de gândire mai scăzut. Barbarus hic ego sum, quia non intelligor illis."

În primul rând, a doua pagină a acestei lucrări nu este împovărată cu nume, prenume, descrieri ale poziției în societate, titluri și elegii în cinstea vreunui prinț avar, a cărui poșetă va fi deschisă cu aceste tămâie - cu amenințarea de a o închide. când laudele se vor termina. Nu veți vedea aici laude respectuoase, scrise cu litere de trei ori mai mari decât textul în sine, adresate celor care au o poziție înaltă în știință, unui patron înțelept - ceva obligatoriu (aș zice inevitabil) pentru cineva la vârstă. de douăzeci care vrea să scrie ceva. Nu spun nimănui de aici că sunt îndatorat sfatului și sprijinului lor pentru toate lucrurile bune din munca mea. Nu spun asta pentru că ar fi o minciună. Dacă ar fi să menționez pe unul dintre cei mari din societate sau din știință (în prezent, diferența dintre aceste două clase de oameni este aproape insesizabilă), jur că nu ar fi un semn de recunoștință. Lor le datorez că am publicat atât de târziu prima dintre aceste două lucrări și că am scris toate acestea în închisoare - într-un loc care cu greu poate fi considerat potrivit pentru reflecția științifică și sunt adesea uimit de reținerea și capacitatea mea de a ține-mi gura pe castel în raport cu Zoils proști și vicioși. Mi se pare că pot folosi cuvântul „Zoile” fără teama de a fi acuzat de indecență, deoarece așa mă refer la adversarii mei. Nu am de gând să scriu aici despre cum și de ce am fost trimis la închisoare, dar trebuie să spun că manuscrisele mele s-au pierdut cel mai adesea pur și simplu în dosarele domnilor academiei, deși, să spun adevărul, nu-mi pot imagina o asemenea indiscreție. din partea oamenilor în a căror conștiință a murit Abel. După părerea mea, oricine ar dori să fie comparat cu acest genial matematician. Este suficient să spunem că articolul meu despre teoria ecuațiilor a fost trimis Academiei de Științe în februarie 1830, că extrasele din acesta au fost trimise în februarie 1829 și, totuși, niciunul din el nu a fost tipărit și chiar manuscrisul s-a dovedit a fi imposibil de revenit.

Galois, prefață inedită, 1832

Pe canalul de youtube al site-ului nostru pentru a fi la curent cu toate noile lecții video.

Mai întâi, să ne amintim formulele de bază ale gradelor și proprietățile lor.

Produsul unui număr A se întâmplă de n ori, putem scrie această expresie ca a a … a=a n

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5. a n b n = (ab) n

7. a n / a m \u003d a n - m

Putere sau ecuații exponențiale- acestea sunt ecuații în care variabilele sunt în puteri (sau exponenți), iar baza este un număr.

Exemple de ecuații exponențiale:

În acest exemplu, numărul 6 este baza, este întotdeauna în partea de jos și variabila X grad sau măsură.

Să dăm mai multe exemple de ecuații exponențiale.
2 x *5=10
16x-4x-6=0

Acum să vedem cum se rezolvă ecuațiile exponențiale?

Să luăm o ecuație simplă:

2 x = 2 3

Un astfel de exemplu poate fi rezolvat chiar și în minte. Se poate observa că x=3. La urma urmei, pentru ca părțile din stânga și din dreapta să fie egale, trebuie să puneți numărul 3 în loc de x.
Acum să vedem cum ar trebui luată această decizie:

2 x = 2 3
x = 3

Pentru a rezolva această ecuație, am eliminat aceleași temeiuri(adică doi) și a notat ce a mai rămas, acestea sunt grade. Am primit răspunsul pe care îl căutam.

Acum să rezumăm soluția noastră.

Algoritm pentru rezolvarea ecuației exponențiale:
1. Trebuie verificat la fel fie că bazele ecuației din dreapta și din stânga. Dacă motivele nu sunt aceleași, căutăm opțiuni pentru a rezolva acest exemplu.
2. După ce bazele sunt aceleași, echivala grad și rezolvați noua ecuație rezultată.

Acum să rezolvăm câteva exemple:

Să începem simplu.

Bazele din stânga și din dreapta sunt egale cu numărul 2, ceea ce înseamnă că putem arunca baza și echivalăm gradele lor.

x+2=4 Cea mai simplă ecuație a rezultat.
x=4 - 2
x=2
Răspuns: x=2

În exemplul următor, puteți vedea că bazele sunt diferite, acestea sunt 3 și 9.

3 3x - 9 x + 8 = 0

Pentru început, le transferăm pe cele nouă în partea dreaptă, obținem:

Acum trebuie să faci aceleași baze. Știm că 9=3 2 . Să folosim formula puterii (a n) m = a nm .

3 3x \u003d (3 2) x + 8

Obținem 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16

3 3x \u003d 3 2x + 16 acum este clar că bazele din stânga și din dreapta sunt aceleași și egale cu trei, ceea ce înseamnă că le putem elimina și echivala gradele.

3x=2x+16 are cea mai simplă ecuație
3x-2x=16
x=16
Răspuns: x=16.

Să ne uităm la următorul exemplu:

2 2x + 4 - 10 4 x \u003d 2 4

În primul rând, ne uităm la baze, bazele sunt diferite două și patru. Și trebuie să fim la fel. Transformăm cvadruplul după formula (a n) m = a nm .

4 x = (2 2) x = 2 2x

Și folosim, de asemenea, o formulă a n a m = a n + m:

2 2x+4 = 2 2x 2 4

Adăugați la ecuație:

2 2x 2 4 - 10 2 2x = 24

Am dat un exemplu din aceleași motive. Dar alte numere 10 și 24 interferează cu noi. Ce să facem cu ele? Dacă te uiți cu atenție, poți vedea că în partea stângă repetăm ​​2 2x, iată răspunsul - putem pune 2 2x din paranteze:

2 2x (2 4 - 10) = 24

Să calculăm expresia dintre paranteze:

2 4 — 10 = 16 — 10 = 6

Împărțim întreaga ecuație la 6:

Imaginează-ți 4=2 2:

2 2x \u003d 2 2 baze sunt aceleași, aruncați-le și egalați gradele.
2x \u003d 2 s-a dovedit a fi cea mai simplă ecuație. Împărțim la 2, obținem
x = 1
Răspuns: x = 1.

Să rezolvăm ecuația:

9 x - 12*3 x +27= 0

Să transformăm:
9 x = (3 2) x = 3 2x

Obtinem ecuatia:
3 2x - 12 3 x +27 = 0

Bazele noastre sunt aceleași, egale cu trei. În acest exemplu, este clar că primul triplu are un grad de două ori (2x) decât al doilea (doar x). În acest caz, puteți decide metoda de substitutie. Numărul cu gradul cel mai mic se înlocuiește cu:

Atunci 3 2x \u003d (3 x) 2 \u003d t 2

Inlocuim toate gradele cu x din ecuatie cu t:

t 2 - 12t + 27 \u003d 0
Obținem o ecuație pătratică. Rezolvăm prin discriminant, obținem:
D=144-108=36
t1 = 9
t2 = 3

Înapoi la Variabilă X.

Luăm t 1:
t 1 \u003d 9 \u003d 3 x

Acesta este,

3 x = 9
3 x = 3 2
x 1 = 2

S-a găsit o rădăcină. Îl căutăm pe al doilea, din t 2:
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x 2 = 1
Răspuns: x 1 \u003d 2; x 2 = 1.

Pe site puteti in sectiunea AJUTA LA DECIZI sa puneti intrebari de interes, va vom raspunde cu siguranta.

Alăturați-vă unui grup

Judecând după începutul publicației, pe care îl vom omite aici, textul a fost scris de Iuri Ignatievici. Și este bine scris, iar problemele sunt de actualitate, așa se numește Rusia, așa cum face Mukhin...

Indiferent cum tratează cineva guvernul anti-popor, Rusia este deasupra lui și nu merită insulte. Chiar și de la talentatul înșelător al agenției americane NASA.

*

Apel la tovarăș. Mukhin Yu.I.

Dragă Iuri Ignatievici!Știu că vizitezi aceste pagini. Prin urmare, mă adresez direct ție.

Cu toții apreciem munca ta dezinteresată în domeniul dezvăluirii minciunilor Occidentului, minciunilor Americii, minciunilor pseudo-oamenilor de știință, minciunile liberalilor. Cu plăcere și folos pentru noi și societate ne gândim la subiectele serioase pe care ni le aruncați din când în când, fie că este vorba despre meritocrație sau metafizică, dragoste pentru istoria națională sau restabilirea justiției.

Cu toate acestea, definițiile tale despre Patria noastră comună cu tine sunt nedumerite și foarte supărate.

Cu toate acestea, judecă singur: cum ai caracteriza o persoană care a început să-și insulte mama care s-a îmbolnăvit și din această cauză a încetat temporar să lucreze?

Dar Rusia, indiferent cum s-ar numi și oricât de bună sau dezgustătoare ar fi puterea, Rusia este Patria noastră. Patrie. Pentru ea, bunicii noștri și-au vărsat sângele și și-au dat viața.

Prin urmare, a-l pune la egalitate cu puterea înseamnă a coborî sublimul spiritual la nivelul materialului, și chiar scăzut. Acestea. compari categorii complet diferite. Un lucru inacceptabil pentru orice persoană sănătoasă la minte.

Te implor, dragă tovarășă. Mukhin, gândește-te serios la asta.

**

... Și cu ecuațiile (nu știam asta), situația este următoarea. Cum să găsiți rădăcinile unei ecuații pătratice a fost ghicit în Egiptul antic.

Cum să găsiți rădăcinile unei ecuații cubice și a unei ecuații de gradul al patrulea a fost găsit în secolul al XVI-lea, dar nu au putut găsi rădăcinile unei ecuații de gradul cinci până în 2016. Și departe de oamenii obișnuiți au încercat.

În secolul al XVI-lea, fondatorul algebrei simbolice François Viet a încercat să găsească rădăcinile ecuației de gradul al cincilea; în secolul al XIX-lea, fondatorul algebrei superioare moderne, matematicianul francez Evariste Galois, a încercat să facă acest lucru; după el , matematicianul norvegian Niels Henrik Abel a încercat să găsească rădăcinile ecuațiilor de gradul al cincilea, care, în final, a renunțat și a demonstrat imposibilitatea rezolvării ecuației de gradul al cincilea într-o formă generală.

Citim în Wikipedia despre meritele lui Abel: „Abel a finalizat un studiu strălucit al unei probleme străvechi:a dovedit imposibilitatea rezolvării într-o formă generală (în radicali) a unei ecuații de gradul 5...

În algebră, Abel a găsit o condiție necesară pentru ca rădăcina unei ecuații să fie exprimată „în radicali” în termeni de coeficienți ai acestei ecuații. Condiția suficientă a fost descoperită curând de Galois, ale cărui realizări s-au bazat pe opera lui Abel.

Abel a dat exemple specifice de ecuație de gradul 5 ale cărei rădăcini nu pot fi exprimate în radicali și, astfel, a închis în mare măsură problema antică.

După cum puteți vedea, dacă au încercat să demonstreze teorema Poincaré tot timpul și Perelman s-a dovedit a avea mai mult succes decât alți matematicieni, atunci după Abel, matematica nu a preluat ecuații de gradul cinci.

Și în 2014 matematician din Tomsk Serghei Zaikov, ceea ce se poate aprecia din fotografie că se află deja în ani de zile, iar conform datelor din articolul despre el, că este absolvent al Facultății de Matematică Aplicată și Cibernetică a Universității de Stat din Tomsk, în cursul activității sale a primit ecuații de gradul cinci. Capat de drum? Da, fundătură! Dar Serghei Zaikov s-a angajat să treacă peste asta.

Și în 2016, a găsit modalități de a rezolva ecuațiile de gradul al cincilea într-o formă generală! A făcut ceea ce matematicienii Galois și Abel au dovedit imposibilitatea.

Am încercat să găsesc informații despre Serghei Zaikov pe Wikipedia, dar la naiba! Despre matematicianul Serghei Zaikov și despre găsirea soluției ecuațiilor de gradul al cincilea de către el fara informatii!

Picantul problemei este dat și de faptul că pentru matematicieni există un analog al Premiului Nobel - Premiul Abel(Nobel a interzis să dea premiul matematicienilor și acum este dat pentru mișcările intestinale matematice, numindu-le „fizică”).

Acest premiu de matematică este în onoarea aceluiași Abel care a dovedit imposibilitatea a ceea ce a făcut Zaikov. Cu toate acestea, autonominalizarea pentru acest premiu nu este permisă. Dar Zaikov este un matematician singur și nu există organizații care l-ar putea nominaliza pentru acest premiu.

Adevărat, avem Academia de Științe, dar la urma urmei, academicienii stau acolo nu pentru dezvoltarea matematicii, ci „pentru a tăia prada”. Cine are nevoie de acest Zaikov acolo?

Ei bine, pentru agențiile de presă, Zaikov nu este Perelman pentru tine! Prin urmare, descoperirea lui Zaikov pentru mass-media nu este o senzație.

Iată că Poroșenko a făcut o greșeală cu ușa - da! Aceasta este o adevărată senzație!

Matematicianul din Tomsk a rezolvat o problemă care nu a putut fi rezolvată timp de două sute de ani

Odată cu apariția algebrei, sarcina sa principală a fost considerată a fi rezolvarea ecuațiilor algebrice. Soluția ecuației de gradul doi era deja cunoscută în Babilon și Egiptul Antic. Trecem prin aceste ecuații la școală. Vă amintiți ecuația x2 + ax + b = 0 și discriminantul?

Serghei Zaikov cu o carte

Soluția ecuațiilor algebrice de gradul al treilea și al patrulea a fost găsită în secolul al XVI-lea. Dar nu a fost posibil să se rezolve ecuația gradului al cincilea. Motivul a fost găsit de Lagrange. El a arătat că soluția ecuațiilor de gradul al treilea și al patrulea a devenit posibilă deoarece acestea pot fi reduse la ecuații care fuseseră deja rezolvate înainte. O ecuație de gradul al treilea poate fi redusă la o ecuație de gradul doi, iar o ecuație de gradul al patrulea poate fi redusă la o ecuație de gradul al treilea. Dar ecuația gradului al cincilea este redusă la ecuația gradului al șaselea, adică mai complexă, astfel încât metodele tradiționale de soluție nu sunt aplicabile.

Problema rezolvării unei ecuații de gradul cinci a avansat cu doar două sute de ani în urmă, când Abel a demonstrat că nu toate ecuațiile de gradul cinci pot fi rezolvate în radicali, adică în rădăcini pătrate, cubice și alte rădăcini cunoscute de la școală. Și Galois în curând, adică acum două sute de ani, a găsit un criteriu pentru a determina ce ecuații de gradul al cincilea pot fi rezolvate în radicali și care nu. Constă în faptul că grupul Galois de ecuații de gradul cinci solubile radical trebuie să fie ciclic sau metaciclic. Dar Galois nu a găsit o modalitate de a rezolva în radicali acele ecuații de gradul cinci care sunt rezolvabile în radicali. Teoria Galois este foarte faimoasă, s-au scris multe cărți despre ea.

Până acum, s-au găsit doar soluții particulare pentru ecuațiile de gradul al cincilea rezolvabile în radicali. Și abia anul acesta, matematicianul din Tomsk Serghei Zaikov a rezolvat o problemă care nu a putut fi rezolvată timp de două sute de ani. A publicat cartea „Cum se rezolvă ecuațiile algebrice de gradul cinci în radicali”, în care a indicat o metodă de rezolvare a oricăror ecuații de gradul cinci care sunt rezolvabile în radicali. Zaikov este absolvent al Facultății de Matematică Aplicată și Cibernetică a Universității de Stat din Tomsk. L-am putut intervieva.

— Serghei, de ce ai început să rezolvi această problemă?

— Aveam nevoie de o soluție la o ecuație de gradul cinci pentru a rezolva o problemă dintr-o altă ramură a matematicii. Am început să-mi dau seama cum să o găsesc și am aflat că nu toate sunt rezolvate în radicali. Apoi am încercat să găsesc în literatura științifică o modalitate de a rezolva acele ecuații care sunt rezolvabile în radicali, dar am găsit doar un criteriu prin care se poate determina care sunt rezolvabile și care nu. Nu sunt algebrist, dar, bineînțeles, ca absolvent al FPMK, pot aplica și metode algebrice. Prin urmare, din 2014, am început serios să caut o soluție și am găsit-o și eu.

Metoda a fost găsită de mine acum doi ani, am pregătit o carte în care nu numai că era descrisă, ci și metode de rezolvare a unor ecuații de grade mai mari decât a cincea. Dar nu am avut bani să-l public. Anul acesta am decis că va fi mai ușor să public doar o parte din această lucrare și am luat doar jumătate din ea, dedicată unei metode de rezolvare a unei ecuații de gradul cinci la radicali.

Mi-am propus să public ceva de genul unui ghid pentru rezolvarea acestei probleme, ușor de înțeles pentru matematicienii care trebuie să rezolve o anumită ecuație. Prin urmare, am simplificat-o eliminând o mulțime de formule lungi și o parte semnificativă a teoriei, reducând-o la mai mult de jumătate, lăsând doar necesarul. Prin urmare, am primit ceva de genul unei cărți „pentru manechine”, conform căreia matematicienii care nu sunt familiarizați cu teoria Galois pot rezolva ecuația de care au nevoie.

- Pentru aceasta, multumiri mult lui Vladislav Beresnev, pe care il cunoastem de multi ani. El a sponsorizat publicarea cărții.

Este posibil să primești vreun premiu la matematică pentru rezolvarea acestei probleme? De exemplu, l-ai menționat pe Abel. Dar există un Premiu Abel în matematică, care este considerat un analog al Premiului Nobel?

„Această posibilitate nu poate fi exclusă complet. Dar nici nu trebuie să speri.

De exemplu, cererile pentru candidații pentru Premiul Abel 2019 trebuie să fie depuse până pe 15 septembrie. Mai mult, autonominalizarea nu este permisă. Sunt un matematician singuratic. Nu există organizații sau matematicieni cunoscuți care să mă nominalizeze. Prin urmare, nu va fi luat în considerare indiferent dacă munca mea merită acest premiu și dacă este în spiritul acestui premiu să fie acordat celor care continuă lucrarea lui Abel. Dar chiar dacă este prezentat, totul depinde și de nivelul de muncă al altor candidați.

Cartea este destinată celor care nu sunt familiarizați cu teoria Galois. Fundamentele teoriei Galois sunt date numai în partea în care sunt necesare pentru rezolvarea ecuației, metoda soluției este descrisă în detaliu și sunt prezentate tehnici care simplifică soluția. O parte semnificativă a cărții este dedicată unui exemplu de rezolvare a unei anumite ecuații. Recenzii cărții sunt doctorul în științe tehnice Gennady Petrovici Agibalov și doctorul în fizică. mat. Științe, profesorul Petr Andreevici Krylov.

PREGĂTIT ANASTASIA SKIRNEVSKAYA

În general, o ecuație care are un grad mai mare de 4 nu poate fi rezolvată în radicali. Dar uneori mai putem găsi rădăcinile polinomului din stânga în ecuația de cel mai înalt grad, dacă îl reprezentăm ca produs de polinoame într-un grad de cel mult 4. Rezolvarea unor astfel de ecuații se bazează pe descompunerea polinomului în factori, așa că vă sfătuim să revizuiți acest subiect înainte de a studia acest articol.

Cel mai adesea, trebuie să se ocupe de ecuații de grade superioare cu coeficienți întregi. În aceste cazuri, putem încerca să găsim rădăcini raționale și apoi factorizarea polinomul astfel încât apoi să-l putem converti într-o ecuație de grad inferior, care va fi ușor de rezolvat. În cadrul acestui material, vom lua în considerare doar astfel de exemple.

Ecuații de grad superior cu coeficienți întregi

Toate ecuațiile de forma a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , putem reduce la o ecuație de același grad înmulțind ambele părți cu a n n - 1 și schimbând variabila de forma y = a n x:

un n x n + un n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 + … + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 + … + b 1 y + b 0 = 0

Coeficienții rezultați vor fi, de asemenea, numere întregi. Astfel, va trebui să rezolvăm ecuația redusă de gradul al n-lea cu coeficienți întregi, care are forma x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Calculăm rădăcinile întregi ale ecuației. Dacă ecuația are rădăcini întregi, trebuie să le căutați printre divizorii termenului liber a 0. Să le notăm și să le substituim în egalitatea originală unul câte unul, verificând rezultatul. Odată ce am obținut o identitate și am găsit una dintre rădăcinile ecuației, o putem scrie sub forma x - x 1 · P n - 1 (x) = 0 . Aici x 1 este rădăcina ecuației, iar P n - 1 (x) este câtul x n + a n x n - 1 + ... + a 1 x + a 0 împărțit la x - x 1 .

Înlocuiți divizorii rămași în P n - 1 (x) = 0 , începând cu x 1 , deoarece rădăcinile pot fi repetate. După obținerea identității, rădăcina x 2 este considerată găsită, iar ecuația poate fi scrisă ca (x - x 1) (x - x 2) P n - 2 (x) \u003d 0. Aici P n - 2 (x ) va fi cât de la împărțirea P n - 1 (x) la x - x 2 .

Continuăm să sortăm prin divizori. Găsiți toate rădăcinile întregi și notați numărul lor ca m. După aceea, ecuația inițială poate fi reprezentată ca x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Aici P n - m (x) este un polinom de gradul n - m --lea. Pentru calcul este convenabil să folosiți schema lui Horner.

Dacă ecuația noastră originală are coeficienți întregi, nu putem ajunge la rădăcini fracționale.

Ca rezultat, am obținut ecuația P n - m (x) = 0, ale cărei rădăcini pot fi găsite în orice mod convenabil. Ele pot fi iraționale sau complexe.

Să arătăm pe un exemplu specific cum se aplică o astfel de schemă de soluții.

Exemplul 1

Condiție: găsiți soluția ecuației x 4 + x 3 + 2 x 2 - x - 3 = 0 .

Soluţie

Să începem cu găsirea rădăcinilor întregi.

Avem o interceptare egală cu minus trei. Are divizori egali cu 1 , - 1 , 3 si - 3 . Să le substituim în ecuația originală și să vedem care dintre ele va da identități ca rezultat.

Pentru x egal cu unu, obținem 1 4 + 1 3 + 2 1 2 - 1 - 3 \u003d 0, ceea ce înseamnă că unul va fi rădăcina acestei ecuații.

Acum să împărțim polinomul x 4 + x 3 + 2 x 2 - x - 3 la (x - 1) într-o coloană:

Deci x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Am obținut o identitate, ceea ce înseamnă că am găsit o altă rădăcină a ecuației, egală cu - 1.

Împărțim polinomul x 3 + 2 x 2 + 4 x + 3 la (x + 1) într-o coloană:

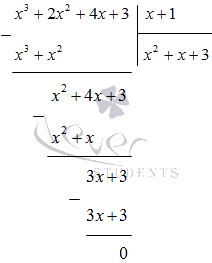
Înțelegem asta

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Inlocuim urmatorul divizor in ecuatia x 2 + x + 3 = 0, incepand de la - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Egalitățile rezultate vor fi incorecte, ceea ce înseamnă că ecuația nu mai are rădăcini întregi.

Rădăcinile rămase vor fi rădăcinile expresiei x 2 + x + 3 .

D \u003d 1 2 - 4 1 3 \u003d - 11< 0

De aici rezultă că acest trinom pătrat nu are rădăcini reale, dar există conjugate complexe: x = - 1 2 ± i 11 2 .

Să lămurim că în loc să ne împărțim într-o coloană, se poate folosi schema lui Horner. Acest lucru se face astfel: după ce am determinat prima rădăcină a ecuației, completăm tabelul.

În tabelul de coeficienți, putem vedea imediat coeficienții coeficienților din împărțirea polinoamelor, ceea ce înseamnă x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

După ce găsim următoarea rădăcină, egală cu - 1, obținem următoarele:

Răspuns: x \u003d - 1, x \u003d 1, x \u003d - 1 2 ± i 11 2.

Exemplul 2

Condiție: rezolvați ecuația x 4 - x 3 - 5 x 2 + 12 = 0.

Soluţie

Membrul liber are divizori 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .

Să le verificăm în ordine:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Deci x = 2 va fi rădăcina ecuației. Împărțiți x 4 - x 3 - 5 x 2 + 12 la x - 2 folosind schema lui Horner:

Ca rezultat, obținem x - 2 (x 3 + x 2 - 3 x - 6) = 0 .

2 3 + 2 2 - 3 2 - 6 = 0

Deci 2 va fi din nou o rădăcină. Împărțiți x 3 + x 2 - 3 x - 6 = 0 la x - 2:

Ca rezultat, obținem (x - 2) 2 (x 2 + 3 x + 3) = 0 .

Verificarea divizorilor rămași nu are sens, deoarece egalitatea x 2 + 3 x + 3 = 0 este mai rapidă și mai convenabilă de rezolvat folosind discriminantul.

Să rezolvăm ecuația pătratică:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Obținem o pereche complexă de rădăcini conjugate: x = - 3 2 ± i 3 2 .

Răspuns: x = - 3 2 ± i 3 2 .

Exemplul 3

Condiție: găsiți rădăcinile reale pentru ecuația x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Soluţie

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Efectuăm înmulțirea 2 3 a ambelor părți ale ecuației:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Înlocuim variabilele y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Ca rezultat, am obținut o ecuație standard de gradul 4, care poate fi rezolvată conform schemei standard. Să verificăm divizorii, să împărțim și în final obținem că are 2 rădăcini reale y \u003d - 2, y \u003d 3 și două complexe. Nu vom prezenta aici întreaga soluție. În virtutea înlocuirii, rădăcinile reale ale acestei ecuații vor fi x = y 2 = - 2 2 = - 1 și x = y 2 = 3 2 .

Răspuns: x 1 \u003d - 1, x 2 \u003d 3 2

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter