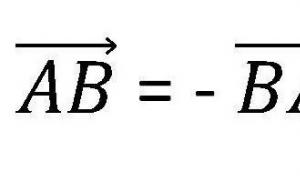Teoria despre modificarea energiei cinetice a unui sistem mecanic. Teorema privind modificarea energiei cinetice. Un exemplu de rezolvare a problemei. Legea privind schimbarea energiei mecanice

sistem mecanic

Energia cinetică a unui sistem mecanic se numește suma aritmetică a energiilor cinetice ale tuturor punctelor sale materiale

Calculul energiei cinetice a unui solid

1. Mișcare de translație

După cum se știe, cu mișcarea de translație, vitezele tuturor punctelor corpului în același moment sunt egale, atunci (83) poate fi reprezentat sub forma

. (84)

Cu mișcarea de translație a unui corp, energia sa cinetică este egală cu jumătate din produsul masei cu pătratul vitezei centrului de masă.

2. Mișcarea de rotație a unui corp rigid

P Cu o mișcare de rotație, viteza fiecărui punct al corpului

. (85)

Înlocuitor (85) în (83):

.

Ținând cont de (59), obținem

. (86)

În timpul mișcării de rotație, energia cinetică este egală cu jumătate din produsul momentului de inerție al corpului față de axa de rotație cu pătratul vitezei unghiulare.

3 ... Mișcarea avionului

Mișcarea plană poate fi reprezentată ca rotație în jurul polului (de exemplu, centrul de masă) și mișcarea împreună cu polul, apoi

. (87)

Energia cinetică a unui corp în mișcare plană este egală cu suma energiilor cinetice din mișcarea de translație împreună cu centrul de masă și mișcarea de rotație față de centrul de masă.

Teorema: Modificarea energiei cinetice a unui sistem mecanic la o parte din deplasarea sa este egală cu suma muncii tuturor forțelor interne și externe ale sistemului la aceeași deplasare.

. (88)

Observatii:

1. Valoarea introdusă a energiei cinetice a sistemului, în contrast cu impulsul sistemului și momentul unghiular, este o mărime scalară. în care:

Q= 0 pentru mișcarea de rotație și repaus;

K O= 0 pentru mișcarea de translație sau în repaus;

T

Astfel, spre deosebire de teorema despre modificarea momentului și a momentului unghiular, această teoremă este potrivită pentru studiul oricărui tip de mișcare, deoarece T= 0 numai pentru un sistem staționar.

2. Spre deosebire de teoremele menționate mai sus, această teoremă ține cont de acțiunea forțelor interne ale sistemului.

Unele cazuri de calcul al muncii

1. Lucrarea momentului de forțăM Zîn jurul axei este egal cu produsul momentului și unghiului de rotație  corp în jurul axei

. (89)

2. Suma muncii forțelor interne un corp absolut rigid (nedeformabil) este întotdeauna zero.

3. Lucrări de frecare la rulare
.

,

Unde  - coeficient de frecare la rulare;

R- raza cilindrului;

s- lungimea arcului, egală cu segmentul de drum parcurs de centrul de masă C de-a lungul suprafeţei;


- unghiul de rotatie al axelor cilindrilor in timpul miscarii;

N- reactie normala la suprafata;

P- gravitatie;

F tr- forta de frecare de alunecare.

Ecuații diferențiale pentru mișcarea de translație, rotație și plană a unui corp rigid

1. Mișcare de translație

În timpul mișcării de translație, toate punctele corpului se mișcă pe aceleași traiectorii și în același moment au aceleași accelerații. Apoi, pentru a descrie mișcarea, se poate folosi teorema privind mișcarea centrului de masă (67). Proiectăm această ecuație pe axele de coordonate

Sistemul (90) este ecuațiile diferențiale ale mișcării de translație a unui corp rigid.

2. Mișcare de rotație

P gura unui corp solid se rotește în jurul unei axe sub acțiunea forțelor. Caracteristica dinamică a mișcării de rotație a unui corp rigid este momentul cinetic K z, iar caracteristica acțiunii de rotație a forței este momentul forței în jurul axei. Prin urmare, pentru a descrie mișcarea de rotație a unui corp rigid în raport cu o axă fixă, folosim teorema privind modificarea momentului unghiular (81)

. (91)

Mișcare de rotație
, atunci

,

având în vedere că eu z= const, ca rezultat obținem

. (92)

Ecuația (92) este o ecuație diferențială pentru mișcarea de rotație a unui corp rigid în jurul unei axe fixe.

Colț găsit  va determina poziția corpului care efectuează în orice moment mișcarea de rotație.

3. Mișcarea avionului

Poziția unui corp care efectuează o mișcare plană în orice moment este determinată de poziția stâlpului și de unghiul de rotație al corpului față de pol. Dacă centrul de masă al corpului este luat drept pol, atunci ecuația mișcării acestuia poate fi găsită prin teorema privind mișcarea centrului de masă (67), iar mișcarea de rotație în jurul centrului va fi determinată de ecuație. (92), care este valabil și pentru mișcarea sistemului în jurul axei care trece prin centrul de masă. Atunci ecuațiile diferențiale ale mișcării plane a unui corp rigid au forma

Forma integrală (finală).... Teorema privind modificarea energiei cinetice a unui punct material: modificarea energiei cinetice a unui punct material la o parte din deplasarea sa este egală cu suma algebrică a muncii tuturor forțelor care acționează asupra acestui punct la aceeași deplasare.

Teorema privind modificarea energiei cinetice a unui sistem mecanic este formulată: modificarea energiei cinetice a unui sistem mecanic atunci când se deplasează dintr-o poziție în alta este egală cu suma muncii tuturor culilor externi și interni aplicați sistemului în această mișcare:

În cazul unui sistem neschimbabil, suma muncii forțelor interne asupra oricărei deplasări este egală cu zero (), atunci

Legea conservării energiei mecanice. Când un sistem mecanic se mișcă sub acțiunea unor forțe care au un potențial, modificările energiei cinetice a sistemului sunt determinate de dependențe:

Unde ,

Se numește suma energiilor cinetice și potențiale ale sistemului energie mecanică deplină sisteme.

În acest fel, atunci când un sistem mecanic se mișcă într-un câmp potențial staționar, energia mecanică totală a sistemului în timpul mișcării rămâne neschimbată.

Sarcină. Un sistem mecanic sub influența gravitației începe să se miște dintr-o stare de repaus. Ținând cont de frecarea de alunecare a corpului 3, neglijând alte forțe de rezistență și masele firelor, presupuse a fi inextensibile, se determină viteza și accelerația corpului 1 în momentul în care traiectoria parcursă de acesta devine egală cu s(fig. 3.70).

În sarcină, acceptați:

Soluţie. Sistemul mecanic este actionat de forte active,,. Aplicând principiul eliberării sistemului de constrângeri, vom arăta reacțiile suportului articulat-fix 2 și o suprafață înclinată brută. Direcțiile vitezelor corpurilor sistemului vor fi descrise ținând cont de faptul că corpul 1 este descendent.

Rezolvăm problema folosind teorema privind modificarea energiei cinetice a unui sistem mecanic:

Unde Tși - energia cinetică a sistemului în pozițiile inițiale și finale; - suma algebrică a muncii forţelor exterioare aplicate sistemului, asupra deplasării sistemului din poziţia iniţială în cea finală; - suma muncii forțelor interne ale sistemului pe aceeași deplasare.

Pentru sistemul luat în considerare, format din corpuri absolut rigide legate prin filete inextensibile:

Din moment ce sistemul era în repaus în poziția inițială, atunci. Prin urmare:

Energia cinetică a sistemului este suma energiilor cinetice ale corpurilor 1, 2, 3:

Energia cinetică a sarcinii 1, care se deplasează translațional, este egală cu:

Energia cinetică a blocului 2, care se rotește în jurul axei Оz, perpendicular pe planul desenului:

Energia cinetică a corpului 3 în mișcarea sa de translație:

În acest fel,

Expresia pentru energia cinetică conține vitezele necunoscute ale tuturor corpurilor din sistem. Este necesar să începem definiția cu. Să scăpăm de necunoscutele inutile alcătuind ecuațiile conexiunilor.

Ecuațiile de constrângere nu sunt altceva decât relațiile cinematice dintre vitezele și deplasările punctelor din sistem. La elaborarea ecuațiilor de constrângeri, vom exprima toate vitezele și deplasările necunoscute ale corpurilor sistemului în termeni de viteză și deplasare a sarcinii 1.

Viteza oricărui punct al jantei cu rază mică este egală cu viteza corpului 1, precum și produsul dintre viteza unghiulară a corpului 2 și raza de rotație r:

De aici exprimăm viteza unghiulară a corpului 2:

Viteza de rotație a oricărui punct al marginii unui bloc cu rază mare, pe de o parte, este egală cu produsul dintre viteza unghiulară a blocului și raza de rotație și, pe de altă parte, viteza corpului. 3:

Înlocuind valoarea vitezei unghiulare, obținem:

După ce am integrat expresiile (a) și (b) în condițiile inițiale, notăm raportul deplasărilor punctelor sistemului:

Cunoscând dependențele de bază ale vitezelor punctelor sistemului, să revenim la expresia energiei cinetice și să substituim ecuațiile (a) și (b) în ea:

Momentul de inerție al corpului 2 este:

Înlocuind valorile maselor corpurilor și ale momentului de inerție al corpului 2, scriem:

Determinarea sumei muncii tuturor forțelor externe ale sistemului la o deplasare dată.

Acum, conform teoremei privind modificarea energiei cinetice a unui sistem mecanic, echivalăm valorile Tși

Viteza corpului 1 se obține din expresia (g)

Accelerația corpului 1 poate fi determinată prin diferențierea egalității (r) în timp.

Vedere: acest articol a fost citit de 49.915 ori

Pdf Selectează limba... rusă ucraineană engleză

Scurtă recenzie

Întregul material este descărcat mai sus, având selectat în prealabil limba

Două cazuri de transformare a mișcării mecanice a unui punct material sau a unui sistem de puncte:

1. mișcarea mecanică este transferată de la un sistem mecanic la altul ca mișcare mecanică;
2. mișcarea mecanică se transformă într-o altă formă de mișcare a materiei (sub formă de energie potențială, căldură, electricitate etc.).

Când se consideră transformarea mișcării mecanice fără trecerea acesteia la o altă formă de mișcare, măsura mișcării mecanice este vectorul impulsului unui punct material sau al unui sistem mecanic. Măsura acțiunii forței în acest caz este vectorul impulsului forței.

Când mișcarea mecanică se transformă într-o altă formă de mișcare a materiei, energia cinetică a unui punct material sau a unui sistem mecanic acționează ca o măsură a mișcării mecanice. Măsura acțiunii forței atunci când o mișcare mecanică este transformată într-o altă formă de mișcare este munca forței

Energie kinetică

Energia cinetică este capacitatea corpului de a depăși obstacolele în timpul mișcării.

Energia cinetică a unui punct material

Energia cinetică a unui punct material este o mărime scalară care este egală cu jumătate din produsul masei punctului cu pătratul vitezei sale.

Energie kinetică:

• caracterizează atât mișcările de translație, cât și de rotație;
• nu depinde de direcția de mișcare a punctelor sistemului și nu caracterizează schimbarea în aceste direcții;
• caracterizează acţiunea atât a forţelor interne cât şi a celor externe.

Energia cinetică a unui sistem mecanic

Energia cinetică a sistemului este egală cu suma energiilor cinetice ale corpurilor sistemului. Energia cinetică depinde de tipul de mișcare al corpurilor sistemului.

Determinarea energiei cinetice a unui corp rigid pentru diferite tipuri de mișcare.

Energia cinetică a mișcării de translație
În mișcarea de translație, energia cinetică a corpului este T=m V 2/2.

Masa este o măsură a inerției corpului în timpul mișcării de translație.

Energia cinetică a mișcării de rotație a corpului

În timpul mișcării de rotație a corpului, energia cinetică este egală cu jumătate din produsul momentului de inerție al corpului față de axa de rotație și pătratul vitezei sale unghiulare.

Măsura inerției unui corp în timpul mișcării de rotație este momentul de inerție.

Energia cinetică a unui corp nu depinde de direcția de rotație a corpului.

Energia cinetică a mișcării corpului plan-paralel

Cu mișcarea plan-paralelă a corpului, energia cinetică este

Munca de forta

Lucrul forței caracterizează acțiunea forței asupra corpului la o anumită deplasare și determină modificarea modulului vitezei punctului de mișcare.

Muncă elementară de forță

Lucrul elementar al forței este definit ca o mărime scalară egală cu produsul proiecției forței de tangenta la traiectorie, îndreptată în direcția de mișcare a punctului, și deplasarea infinitezimală a punctului, îndreptată de-a lungul acestui tangentă.

Forța de lucru la deplasarea finală

Munca forței asupra deplasării finale este egală cu suma muncii acesteia pe secțiuni elementare.

Lucrul forței asupra deplasării finale M 1 M 0 este egal cu integrala de-a lungul acestei deplasări din munca elementară.

Lucrul forței asupra deplasării M 1 M 2 este reprezentat de aria figurii delimitată de axa absciselor, curba și ordonatele corespunzătoare punctelor M 1 și M 0.

Unitatea de măsură a forței de muncă și a energiei cinetice în SI 1 (J).

Teoreme de lucru al forțelor

Teorema 1... Lucrul forței rezultante la o anumită deplasare este egal cu suma algebrică a muncii forțelor constitutive la aceeași deplasare.

Teorema 2. Munca unei forțe constante asupra deplasării rezultate este egală cu suma algebrică a muncii acestei forțe asupra deplasărilor componente.

Putere

Puterea este o mărime care determină munca forței pe unitatea de timp.

Unitatea de măsură a puterii este 1W = 1 J/s.

Cazuri de determinare a muncii forţelor

Munca forțelor interne

Suma muncii forțelor interne ale unui corp rigid asupra oricărei deplasări ale acestuia este egală cu zero.

Munca gravitatiei

Lucru cu forța elastică

Lucrul cu forța de frecare

Lucrul forțelor aplicate unui corp în rotație

Lucrul elementar al forțelor aplicate unui corp rigid care se rotește în jurul unei axe fixe este egal cu produsul momentului principal al forțelor externe față de axa de rotație cu creșterea unghiului de rotație.

Rezistență la rostogolire

În zona de contact a cilindrului staționar și a planului, are loc o deformare locală a compresiei de contact, solicitarea este distribuită conform unei legi eliptice și linia de acțiune a rezultatului N a acestor tensiuni coincide cu linia de acțiune a sarcinii. forță asupra cilindrului Q. Când cilindrul se rostogolește, distribuția sarcinii devine asimetrică cu un maxim deplasat spre direcția de mișcare. Rezultatul N este deplasat cu valoarea k - brațul forței de frecare de rulare, care se mai numește și coeficient de frecare de rulare și are dimensiunea lungimii (cm)

Teorema privind modificarea energiei cinetice a unui punct material

Modificarea energiei cinetice a unui punct material la o parte din deplasarea sa este egală cu suma algebrică a robotului tuturor forțelor care acționează asupra punctului la aceeași deplasare.

Teorema privind modificarea energiei cinetice a unui sistem mecanic

Modificarea energiei cinetice a unui sistem mecanic la o anumită deplasare este egală cu suma algebrică a forțelor interne și externe ale robotului care acționează asupra punctelor materiale ale sistemului la aceeași deplasare.

Teorema privind modificarea energiei cinetice a unui corp rigid

Modificarea energiei cinetice a unui corp rigid (sistem neschimbat) la o anumită deplasare este egală cu suma forțelor externe ale robotului care acționează asupra punctelor sistemului la aceeași deplasare.

Eficienţă

Forțe care acționează în mecanisme

Forțele și perechile de forțe (momente) care sunt aplicate unui mecanism sau mașină pot fi împărțite în grupuri:

1. Forțe motrice și momente care efectuează un lucru pozitiv (aplicate la legăturile de antrenare, de exemplu, presiunea gazului pe un piston într-un motor cu ardere internă).

2. Forțe și momente de rezistență care efectuează muncă negativă:

• rezistență utilă (efectuează munca cerută de la mașină și sunt aplicate pe legăturile antrenate, de exemplu, rezistența sarcinii ridicate de mașină),
• forțe de rezistență (de exemplu, forțe de frecare, rezistență a aerului etc.).

3. Forțele de gravitație și forțele de elasticitate ale arcurilor (atât lucru pozitiv, cât și negativ, în timp ce lucrul pentru un ciclu complet este egal cu zero).

4. Forțe și momente aplicate corpului sau rafturii din exterior (reacția fundației etc.), care nu efectuează lucru.

5. Forțe de interacțiune între legături, care acționează în perechi cinematice.

6. Forțele de inerție ale legăturilor, cauzate de masa și mișcarea legăturilor cu accelerație, pot efectua muncă pozitivă, negativă și nu face muncă.

Munca forțelor în mecanisme

În starea constantă de funcționare a mașinii, energia sa cinetică nu se modifică, iar suma muncii forțelor motrice și a forțelor de rezistență aplicate acesteia este egală cu zero.

Munca depusă la punerea în mișcare a mașinii este cheltuită în depășirea rezistențelor utile și dăunătoare.

Eficiența mecanismelor

Eficiența mecanică în mișcare constantă este egală cu raportul dintre munca utilă a mașinii și munca cheltuită la punerea în mișcare a mașinii:

Elementele mașinii pot fi conectate în serie, paralel și mixte.

Eficiență în conexiune în serie

Cu o conexiune în serie de mecanisme, eficiența generală este mai mică cu cea mai scăzută eficiență a unui mecanism individual.

Eficiență cu conexiune paralelă

Cu conexiunea paralelă a mecanismelor, eficiența globală este mai mare decât cea mai mică și mai mică decât cea mai mare eficiență a unui mecanism individual.

Format: pdf

Limba: rusă, ucraineană

Un exemplu de calcul al unui angrenaj drept
Un exemplu de calcul al unui angrenaj drept. S-au efectuat alegerea materialului, calculul tensiunilor admisibile, calculul rezistenței la contact și la încovoiere.

Un exemplu de rezolvare a problemei de îndoire a unei grinzi
În exemplu, sunt construite diagrame ale forțelor tăietoare și ale momentelor încovoietoare, se găsește o secțiune periculoasă și se selectează o grindă în I. Problema analizează construcția diagramelor folosind dependențe diferențiale, se efectuează o analiză comparativă a diferitelor secțiuni transversale ale grinzii.

Un exemplu de rezolvare a problemei torsiunii arborelui
Sarcina este de a verifica rezistența unui arbore de oțel pentru un diametru, material și tensiuni admisibile date. În timpul rezolvării, sunt reprezentate diagrame ale cuplurilor, tensiunilor tăietoare și unghiurilor de torsiune. Greutatea proprie a arborelui nu este luată în considerare.

Un exemplu de rezolvare a problemei de tensiune-comprimare a unei bare
Sarcina este de a verifica rezistența unei bare de oțel la o anumită tensiune admisibilă. În cursul soluției, sunt reprezentate diagrame ale forțelor longitudinale, tensiunilor normale și deplasărilor. Greutatea proprie a barei nu este luată în considerare.

Aplicarea teoremei de conservare a energiei cinetice
Un exemplu de rezolvare a problemei privind aplicarea teoremei privind conservarea energiei cinetice a unui sistem mecanic

Energie se numește o mărime fizică scalară, care este o singură măsură a diferitelor forme de mișcare a materiei și o măsură a tranziției mișcării materiei de la o formă la alta.

Pentru a caracteriza diversele forme de mișcare a materiei se introduc tipuri adecvate de energie, de exemplu: mecanică, internă, energie electrostatică, interacțiuni intranucleare etc.

Energia se supune legii conservării, care este una dintre cele mai importante legi ale naturii.

Energia mecanică E caracterizează mișcarea și interacțiunea corpurilor și este o funcție a vitezelor și a aranjamentului reciproc al corpurilor. Este egală cu suma energiilor cinetice și potențiale.

Energie kinetică

Luați în considerare cazul când un corp cu masă m există o forță constantă \ (~ \ vec F \) (poate fi rezultanta mai multor forțe), iar vectorii forță \ (~ \ vec F \) și deplasările \ (~ \ vec s \) sunt direcționați de-a lungul unei drepte linie într-o singură direcție. În acest caz, munca forței poate fi definită ca A = F∙s... Modulul de forță conform celei de-a doua legi a lui Newton este F = m ∙ a, și modulul de deplasare s cu mișcare rectilinie uniform accelerată, este conectată cu modulele inițialei υ 1 si finala υ 2 viteze si acceleratii A expresia \ (~ s = \ frac (\ upsilon ^ 2_2 - \ upsilon ^ 2_1) (2a) \).

De aici, pentru muncă, primim

\ (~ A = F \ cdot s = m \ cdot a \ cdot \ frac (\ upsilon ^ 2_2 - \ upsilon ^ 2_1) (2a) = \ frac (m \ cdot \ upsilon ^ 2_2) (2) - \ frac (m \ cdot \ upsilon ^ 2_1) (2) \). (unu)

Se numește o mărime fizică egală cu jumătate din produsul masei unui corp cu pătratul vitezei sale energia cinetică a corpului.

Energia cinetică este indicată prin literă E k.

\ (~ E_k = \ frac (m \ cdot \ upsilon ^ 2) (2) \). (2)

Atunci egalitatea (1) poate fi scrisă după cum urmează:

\ (~ A = E_ (k2) - E_ (k1) \). (3)

Teorema energiei cinetice

munca forțelor rezultante aplicate corpului este egală cu modificarea energiei cinetice a corpului.

Deoarece modificarea energiei cinetice este egală cu munca forței (3), energia cinetică a corpului este exprimată în aceleași unități ca și lucrul, adică în jouli.

Dacă viteza iniţială de mişcare a unui corp cu o masă m este egal cu zero și corpul își crește viteza până la valoarea υ , atunci munca forței este egală cu valoarea finală a energiei cinetice a corpului:

\ (~ A = E_ (k2) - E_ (k1) = \ frac (m \ cdot \ upsilon ^ 2) (2) - 0 = \ frac (m \ cdot \ upsilon ^ 2) (2) \). (4)

Semnificația fizică a energiei cinetice

energia cinetică a unui corp care se mișcă cu o viteză υ arată ce lucru trebuie efectuat de o forță care acționează asupra unui corp în repaus pentru a-i conferi această viteză.

Energie potențială

Energie potențială Este energia de interacțiune a corpurilor.

Energia potențială a unui corp ridicat deasupra Pământului este energia de interacțiune dintre corp și Pământ prin forțele gravitaționale. Energia potențială a unui corp deformat elastic este energia de interacțiune a părților individuale ale corpului între ele prin forțe elastice.

Potenţial sunt numite putere, al cărui lucru depinde numai de poziția inițială și finală a unui punct sau corp material în mișcare și nu depinde de forma traiectoriei.

Cu o traiectorie închisă, munca forței potențiale este întotdeauna zero. Forțele potențiale includ forțele gravitaționale, forțele elastice, forțele electrostatice și unele altele.

Forțe al căror lucru depinde de forma traiectoriei se numesc nepotenţial... Când un punct sau un corp material se mișcă de-a lungul unei traiectorii închise, munca forței nepotențiale nu este zero.

Energia potențială de interacțiune a corpului cu Pământul

Găsirea muncii făcute de gravitație F t la deplasarea unui corp cu o masă m vertical în jos de la înălțime h 1 deasupra suprafeței Pământului până la o înălțime h 2 (fig. 1). Dacă diferența h 1 – h 2 este neglijabilă în comparație cu distanța până la centrul Pământului, apoi cu forța gravitațională F m în timpul mișcării corpului poate fi considerat constant și egal mg.

Deoarece deplasarea coincide în direcție cu vectorul gravitației, lucrul gravitației este

\ (~ A = F \ cdot s = m \ cdot g \ cdot (h_1 - h_2) \). (5)

Să luăm acum în considerare mișcarea unui corp de-a lungul unui plan înclinat. Când corpul se mișcă în jos pe un plan înclinat (Fig. 2), forța gravitației F t = m ∙ g lucrând

\ (~ A = m \ cdot g \ cdot s \ cdot \ cos \ alpha = m \ cdot g \ cdot h \), (6)

Unde h- înălțimea planului înclinat, s- modul de deplasare egal cu lungimea planului înclinat.

Mișcarea corpului dintr-un punct V exact CU de-a lungul oricărei traiectorii (Fig. 3) poate fi reprezentat mental ca fiind constând din deplasări de-a lungul secțiunilor de planuri înclinate cu diferite înălțimi h’, h'' etc. Lucru A gravitația tot drumul de la V v CU este egală cu suma lucrărilor pe secțiuni separate ale pistei:

\ (~ A = m \ cdot g \ cdot h "+ m \ cdot g \ cdot h" "+ \ ldots + m \ cdot g \ cdot h ^ n = m \ cdot g \ cdot (h" + h "" + \ ldots + h ^ n) = m \ cdot g \ cdot (h_1 - h_2) \), (7)

Unde h 1 și h 2 - înălțimi față de suprafața Pământului, la care sunt situate, respectiv, punctele Vși CU.

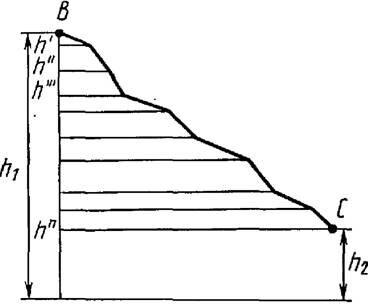
Egalitatea (7) arată că munca forței gravitaționale nu depinde de traiectoria corpului și este întotdeauna egală cu produsul dintre modulul forței gravitaționale cu diferența de înălțimi în pozițiile inițiale și finale.

Când vă deplasați în jos, munca gravitației este pozitivă; când vă deplasați în sus, este negativă. Lucrul gravitației pe o cale închisă este zero.

Egalitatea (7) poate fi reprezentată după cum urmează:

\ (~ A = - (m \ cdot g \ cdot h_2 - m \ cdot g \ cdot h_1) \). (opt)

Mărimea fizică egală cu produsul dintre masa corpului prin modulul de accelerație al gravitației și înălțimea la care corpul este ridicat deasupra suprafeței Pământului se numește energie potențială interacțiunea dintre organism și Pământ.

Lucrul gravitației la mișcarea unui corp cu masă m dintr-un punct situat la înălţime h 2, până la un punct situat la înălțime h 1 de la suprafața Pământului, de-a lungul oricărei traiectorii este egală cu modificarea energiei potențiale de interacțiune dintre corp și Pământ, luată cu semnul opus.

\ (~ A = - (E_ (p2) - E_ (p1)) \). (9)

Energia potențială este indicată prin literă E p.

Valoarea energiei potențiale a unui corp ridicat deasupra Pământului depinde de alegerea nivelului zero, adică de înălțimea la care energia potențială este considerată zero. De obicei, se presupune că energia potențială a unui corp de pe suprafața Pământului este zero.

Cu această alegere a nivelului zero, energia potențială E p unui corp la înălțime h deasupra suprafeței Pământului, este egal cu produsul masei m a corpului cu modulul de accelerație gravitațională g si distanta h de la suprafața Pământului:

\ (~ E_p = m \ cdot g \ cdot h \). (10)

Semnificația fizică a energiei potențiale de interacțiune a corpului cu Pământul

energia potențială a corpului, asupra căreia se acționează forța gravitației, este egală cu munca efectuată de forța gravitațională atunci când corpul se deplasează la nivelul zero.

Spre deosebire de energia cinetică a mișcării de translație, care poate avea doar valori pozitive, energia potențială a unui corp poate fi atât pozitivă, cât și negativă. Masa corpului m la altitudine h, Unde h < h 0 (h 0 - înălțime zero), are energie potențială negativă:

\ (~ E_p = -m \ cdot g \ cdot h \).

Energia potențială a interacțiunii gravitaționale

Energia potențială a interacțiunii gravitaționale a unui sistem de două puncte materiale cu mase mși M de la distanță r unul de celălalt, este egal cu

\ (~ E_p = G \ cdot \ frac (M \ cdot m) (r) \). (unsprezece)

Unde G Este constanta gravitațională și zero al energiei potențiale ( E p = 0) se adoptă la r = ∞.

Energia potențială a interacțiunii gravitaționale a unui corp cu masa m cu Pământul unde h- înălțimea corpului deasupra suprafeței Pământului, M e este masa Pământului, R e este raza Pământului, iar zero al energiei potențiale este ales la h = 0.

\ (~ E_e = G \ cdot \ frac (M_e \ cdot m \ cdot h) (R_e \ cdot (R_e + h)) \). (12)

În aceeași condiție pentru alegerea referinței zero, energia potențială a interacțiunii gravitaționale a unui corp cu masa m cu Pământ pentru înălțimi mici h (h « R e) egal

\ (~ E_p = m \ cdot g \ cdot h \),

unde \ (~ g = G \ cdot \ frac (M_e) (R ^ 2_e) \) este modulul de accelerație gravitațională lângă suprafața Pământului.

Energia potențială a unui corp deformat elastic

Să calculăm munca efectuată de forța elastică atunci când deformația (alungirea) arcului se modifică de la o valoare inițială X 1 până la valoarea finală X 2 (Fig. 4, b, c).

Forța elastică se modifică pe măsură ce arcul se deformează. Pentru a afla munca forței elastice, puteți lua valoarea medie a modulului forței (deoarece forța elastică depinde liniar de X) și înmulțiți cu modulul deplasării:

\ (~ A = F_ (upr-cp) \ cdot (x_1 - x_2) \), (13)

unde \ (~ F_ (upr-cp) = k \ cdot \ frac (x_1 - x_2) (2) \). De aici

\ (~ A = k \ cdot \ frac (x_1 - x_2) (2) \ cdot (x_1 - x_2) = k \ cdot \ frac (x ^ 2_1 - x ^ 2_2) (2) \) sau \ (~ A = - \ stânga (\ frac (k \ cdot x ^ 2_2) (2) - \ frac (k \ cdot x ^ 2_1) (2) \ dreapta) \). (14)

O mărime fizică egală cu jumătate din produsul rigidității unui corp prin pătratul deformării acestuia se numește energie potențială un corp deformat elastic:

\ (~ E_p = \ frac (k \ cdot x ^ 2) (2) \). (15)

Din formulele (14) și (15) rezultă că munca forței elastice este egală cu modificarea energiei potențiale a unui corp deformat elastic, luată cu semnul opus:

\ (~ A = - (E_ (p2) - E_ (p1)) \). (şaisprezece)

Dacă X 2 = 0 și X 1 = X, atunci, după cum se poate vedea din formulele (14) și (15),

\ (~ E_p = A \).

Semnificația fizică a energiei potențiale a unui corp deformat

energia potenţială a unui corp deformat elastic este egală cu munca efectuată de forţa elastică în timpul trecerii corpului la o stare în care deformaţia este nulă.

Energia potențială caracterizează corpurile care interacționează, iar energia cinetică caracterizează corpurile în mișcare. Atât energia potențială, cât și cea cinetică se modifică numai ca urmare a unei astfel de interacțiuni a corpurilor, în care forțele care acționează asupra corpurilor efectuează un alt lucru decât zero. Să luăm în considerare problema schimbărilor de energie în timpul interacțiunilor corpurilor care formează un sistem închis.

Sistem inchis Este un sistem care nu este afectat de forțele externe sau acțiunea acestor forțe este compensată... Dacă mai multe corpuri interacționează între ele numai prin forțe gravitaționale și forțe elastice și nicio forță exterioară nu acționează asupra lor, atunci pentru orice interacțiune a corpurilor, munca forțelor elastice sau forțelor gravitaționale este egală cu modificarea energiei potențiale a corpurilor, luate cu semnul opus:

\ (~ A = - (E_ (p2) - E_ (p1)) \). (17)

Conform teoremei energiei cinetice, munca acelorași forțe este egală cu modificarea energiei cinetice:

\ (~ A = E_ (k2) - E_ (k1) \). (optsprezece)

Dintr-o comparație a egalităților (17) și (18), se poate observa că modificarea energiei cinetice a corpurilor într-un sistem închis este egală în valoare absolută cu modificarea energiei potențiale a sistemului de corpuri și este opusă. la el în semn:

\ (~ E_ (k2) - E_ (k1) = - (E_ (p2) - E_ (p1)) \) sau \ (~ E_ (k1) + E_ (p1) = E_ (k2) + E_ (p2) \). (nouăsprezece)

Legea conservării energiei în procesele mecanice:

suma energiei cinetice și potențiale a corpurilor care alcătuiesc un sistem închis și interacționează între ele prin forțele gravitaționale și forțele elasticității, rămâne constantă.

Se numește suma energiei cinetice și potențiale a corpurilor energie mecanică deplină.

Iată cel mai simplu experiment. Să aruncăm o minge de oțel. După ce am informat viteza inițială υ pornire, îi vom oferi energie cinetică, din cauza căreia va începe să crească în sus. Acțiunea gravitației duce la scăderea vitezei mingii și, prin urmare, a energiei sale cinetice. Dar mingea se ridică din ce în ce mai sus și capătă din ce în ce mai multă energie potențială ( E p = m ∙ g ∙ h). Astfel, energia cinetică nu dispare fără urmă, ci este transformată în energie potențială.

În momentul atingerii punctului de vârf al traiectoriei ( υ = 0) mingea este complet lipsită de energie cinetică ( E k = 0), dar în același timp energia sa potențială devine maximă. Apoi mingea își schimbă direcția de mișcare și se mișcă în jos cu viteza crescândă. Acum are loc transformarea inversă a energiei potențiale în una cinetică.

Legea conservării energiei relevă sens fizic concepte muncă:

munca forțelor gravitaționale și a forțelor elastice, pe de o parte, este egală cu o creștere a energiei cinetice și, pe de altă parte, cu o scădere a energiei potențiale a corpurilor. În consecință, munca este egală cu energia convertită de la un tip la altul.

Legea privind schimbarea energiei mecanice

Dacă sistemul de corpuri care interacționează nu este închis, atunci energia sa mecanică nu este conservată. Modificarea energiei mecanice a unui astfel de sistem este egală cu munca forțelor externe:

\ (~ A_ (vn) = \ Delta E = E - E_0 \). (douăzeci)

Unde Eși E 0 - energiile mecanice totale ale sistemului în starea finală, respectiv inițială.

Un exemplu de astfel de sistem este un sistem în care forțele nepotențiale acționează împreună cu forțele potențiale. Forțele nepotențiale includ forțele de frecare. În cele mai multe cazuri, atunci când unghiul dintre forța de frecare F r corpul este π radian, munca forței de frecare este negativă și egală cu

\ (~ A_ (tr) = -F_ (tr) \ cdot s_ (12) \),

Unde s 12 - calea corpului între punctele 1 și 2.

Forțele de frecare în timpul mișcării sistemului îi reduc energia cinetică. Ca urmare a acestui fapt, energia mecanică a unui sistem închis neconservativ scade întotdeauna, transformându-se în energia formelor de mișcare nemecanice.

De exemplu, o mașină care se deplasează de-a lungul unei secțiuni orizontale a drumului, după ce a oprit motorul, parcurge o anumită distanță și se oprește sub influența forțelor de frecare. Energia cinetică a mișcării de translație a vehiculului a devenit zero, iar energia potențială nu a crescut. În timpul frânării vehiculului s-a produs încălzirea plăcuțelor de frână, a anvelopelor vehiculului și a asfaltului. În consecință, ca urmare a acțiunii forțelor de frecare, energia cinetică a mașinii nu a dispărut, ci s-a transformat în energia internă a mișcării termice a moleculelor.

Legea conservării și transformării energiei

în orice interacțiune fizică, energia este convertită dintr-o formă în alta.

Uneori unghiul dintre forța de frecare F tr și deplasarea elementară Δ r este zero și munca forței de frecare este pozitivă:

\ (~ A_ (tr) = F_ (tr) \ cdot s_ (12) \),

Exemplul 1... Să, forță externă F actioneaza asupra barei V care poate aluneca pe cărucior D(fig. 5). Dacă căruciorul se mișcă spre dreapta, atunci munca forței de frecare de alunecare F tr2 care acționează asupra căruciorului din partea laterală a barei este pozitivă:

Exemplul 2... Când roata rulează, forța sa de frecare de rulare este direcționată de-a lungul mișcării, deoarece punctul de contact al roții cu suprafața orizontală se mișcă în direcția opusă direcției de mișcare a roții, iar munca forței de frecare este pozitivă. (Fig. 6):

Literatură

1. O.F. Kabardin Fizica: Ref. materiale: manual. manual pentru elevi. - M .: Educaţie, 1991 .-- 367 p.
2. Kikoin I.K., Kikoin A.K. Fizica: manual. pentru 9 cl. miercuri shk. - M .: Pro-sveshenie, 1992 .-- 191 p.
3. Manual de fizică elementară: Manual. indemnizatie. În 3 volume / Ed. G.S. Landsberg: vol. 1. Mecanica. Căldură. Fizica moleculară. - M .: Fizmatlit, 2004 .-- 608 p.
4. Yavorskiy B.M., Seleznev Yu.A. Un ghid de referință pentru fizică pentru solicitanții universitari și autoeducație. - M .: Nauka, 1983 .-- 383 p.

Dacă luăm în considerare un punct al sistemului cu masă , având viteză , atunci pentru acest punct va exista

,

unde si - munca elementară a forțelor externe și interne care acționează asupra unui punct. Compunând astfel de ecuații pentru fiecare dintre punctele sistemului și adunându-le termen cu termen, obținem

,

. (2)

Egalitatea exprimă o teoremă privind modificarea energiei cinetice a unui sistem în formă diferențială.

Dacă expresia rezultată este legată de un interval de timp elementar în care s-a produs deplasarea considerată, putem obține o a doua formulare pentru forma diferențială a teoremei: derivata în timp a energiei cinetice a unui sistem mecanic este egală cu suma puterile tuturor forțelor externe () și interne (), adică

Formele diferențiale ale teoremei schimbării energiei cinetice pot fi folosite pentru a compune ecuații diferențiale ale mișcării, dar acest lucru se face destul de rar, deoarece există trucuri mai convenabile.

Avand integrate ambele laturi ale egalitatii (2) in limitele corespunzatoare deplasarii sistemului de la o pozitie initiala, unde energia cinetica este egala, pana la pozitia in care valoarea energiei cinetice devine egala , vom avea

Ecuația rezultată exprimă teorema privind modificarea energiei cinetice în forma finală: modificarea energiei cinetice a sistemului cu o parte din deplasarea sa este egală cu suma muncii asupra acestei deplasări a tuturor forțelor externe și interne aplicate sistemului.

Spre deosebire de teoremele anterioare, forțele interne nu sunt excluse în ecuații. Într-adevăr, dacă și sunt forțele de interacțiune dintre puncte și sistem (vezi Fig. 51), atunci. Dar, în același timp, punctul se poate deplasa spre, iar punctul spre. Lucrul fiecăreia dintre forțe va fi apoi pozitiv și cantitatea de muncă nu va fi zero. Un exemplu este fenomenul rollback. Forțele interne (forțe de presiune) care acționează atât asupra proiectilului, cât și asupra pieselor de rulare înapoi fac o activitate pozitivă aici. Suma acestor lucrări, care nu este egală cu zero, și schimbă energia cinetică a sistemului de la valoarea de la începutul fotografiei la valoarea de la sfârșit.

Un alt exemplu: două puncte legate printr-un arc. Când distanța dintre puncte se schimbă, forțele elastice aplicate punctelor vor face treaba. Dar dacă sistemul constă din corpuri absolut rigide, iar conexiunile dintre ele sunt neschimbabile, nu elastice, ideale, atunci munca forțelor interne va fi egală cu zero și pot fi ignorate și deloc afișate pe diagrama de proiectare.

Luați în considerare două cazuri speciale importante.

1) Sistem imuabil. Imuabil vom numi un sistem în care distanțele dintre punctele de aplicare a forțelor interne nu se modifică atunci când sistemul se mișcă. În special, un astfel de sistem este un corp absolut rigid sau un fir inextensibil.

Fig. 51

Fie două puncte și un sistem neschimbabil (Fig. 51) care acționează unul asupra celuilalt cu forțe și () au viteze și la un moment dat. Apoi pentru o perioadă de timp dt aceste puncte vor face mişcări elementare şi , dirijate de-a lungul vectorilor şi. Dar, deoarece segmentul este neschimbabil, atunci, conform binecunoscutei teoreme a cinematicii, proiecțiile vectorilor și , si, in consecinta, atat deplasarile cat si directia segmentului vor fi egale intre ele, i.e. ... Apoi, munca elementară a forțelor și va fi aceeași ca mărime și opusă ca semn și, în total, vor da zero. Acest rezultat este valabil pentru toate forțele interne pentru orice deplasare a sistemului.

Prin urmare, tragem concluzia că pentru un sistem neschimbabil, suma muncii tuturor forțelor interne este zero iar ecuațiile iau forma

2) Sistem perfect cuplat... Luați în considerare un sistem suprapus cu conexiuni care nu se schimbă în timp. Să împărțim toate forțele externe și interne care acționează asupra punctelor sistemului în activși reacții de legătură. Atunci

,

unde este opera elementară a celor care acţionează asupra k- al treilea punct al sistemului de forțe active externe și interne, a este lucrarea elementară a reacțiilor impuse în același punct de conexiuni externe și interne.

După cum puteți vedea, modificarea energiei cinetice a sistemului depinde de munca și forțele active și reacțiile legăturilor. Cu toate acestea, este posibil să se introducă conceptul de astfel de sisteme mecanice „ideale”, în care prezența legăturilor nu afectează modificarea energiei cinetice a sistemului în timpul mișcării sale. Pentru astfel de conexiuni, trebuie în mod evident îndeplinită următoarea condiție:

Dacă pentru conexiunile care nu se modifică în timp, suma muncii tuturor reacțiilor cu o deplasare elementară a sistemului este egală cu zero, atunci astfel de conexiuni se numesc perfect. Pentru un sistem mecanic, căruia i se impun doar constrângeri ideale care nu se modifică în timp, vom avea evident

Astfel, modificarea energiei cinetice a unui sistem cu legături ideale care nu se modifică în timp pentru nicio deplasare a acestuia este egală cu suma muncii asupra acestei deplasări aplicate sistemului de extern și intern. forte active.

Sistemul mecanic se numeste conservator(energia sa este, parcă, conservată, nu se modifică) dacă integrala energetică

sau (3)

Este legea conservării energiei mecanice: atunci când sistemul se mișcă într-un câmp potențial, energia sa mecanică (suma potențialului și cineticului) rămâne neschimbată, constantă tot timpul.

Un sistem mecanic va fi conservator dacă forțele care acționează asupra lui sunt potențiale, de exemplu, gravitația, forțele elastice. În sistemele mecanice conservatoare, folosind integrala energetică, se poate verifica corectitudinea ecuațiilor diferențiale ale mișcării. Dacă sistemul este conservator și condiția (3) nu este îndeplinită, atunci a fost făcută o eroare în formularea ecuațiilor de mișcare.

Integrala energetică poate fi folosită pentru a verifica corectitudinea ecuațiilor și în alt mod, fără a calcula derivata. Pentru a face acest lucru, după efectuarea integrării numerice a ecuațiilor de mișcare, calculați valoarea energiei mecanice totale pentru două momente diferite în timp, de exemplu, inițial și final. Dacă diferența de valori se dovedește a fi comparabilă cu erorile de calcul, aceasta va indica corectitudinea ecuațiilor utilizate.

Toate teoremele anterioare au făcut posibilă excluderea forțelor interne din ecuațiile de mișcare, dar toate forțele externe, inclusiv reacțiile necunoscute anterior ale conexiunilor externe, au rămas în ecuații. Valoarea practică a teoremei privind modificarea energiei cinetice este că, cu constrângeri ideale care nu se modifică în timp, ne va permite să excludem din ecuațiile mișcării toate reacții de legătură necunoscute anterior.