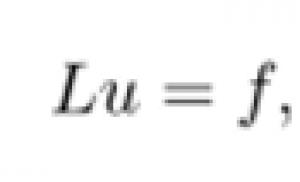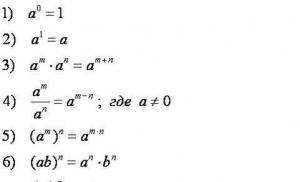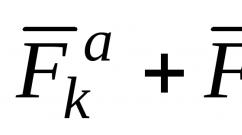Perbedaan skema: skema eksplisit dan implisit. Metode membangun skema perbedaan Menyelesaikan masalah campuran persamaan gelombang menggunakan metode grid

Skema perbedaan

Skema perbedaan- ini adalah sistem persamaan aljabar berhingga, yang dikorespondensikan dengan beberapa masalah diferensial yang berisi persamaan diferensial dan kondisi tambahan (misalnya, kondisi batas dan/atau distribusi awal). Dengan demikian, skema perbedaan digunakan untuk mereduksi suatu masalah diferensial, yang bersifat kontinu, menjadi sistem persamaan berhingga, yang penyelesaian numeriknya pada prinsipnya dapat dilakukan pada komputer. Persamaan aljabar yang dikorespondensikan dengan persamaan diferensial diperoleh dengan menggunakan metode selisih, yang membedakan teori skema selisih dengan metode numerik lainnya untuk menyelesaikan masalah diferensial (misalnya metode proyeksi, seperti metode Galerkin).

Penyelesaian skema selisih disebut penyelesaian perkiraan masalah diferensial.

Meskipun definisi formal tidak memberikan batasan yang signifikan pada jenis persamaan aljabar, dalam praktiknya masuk akal untuk hanya mempertimbangkan skema yang dalam beberapa hal sesuai dengan masalah diferensial. Konsep penting dalam teori skema perbedaan adalah konsep konvergensi, aproksimasi, stabilitas, dan konservatisme.

Perkiraan

Mereka mengatakan bahwa operator diferensial yang didefinisikan pada fungsi-fungsi yang didefinisikan dalam domain didekati pada kelas fungsi tertentu oleh operator perbedaan hingga yang didefinisikan pada fungsi-fungsi yang didefinisikan pada mesh tergantung pada langkah jika

Suatu perkiraan dikatakan berurutan jika

dimana adalah konstanta yang bergantung pada fungsi tertentu, tetapi tidak bergantung pada langkah. Norma yang digunakan di atas mungkin berbeda, dan konsep perkiraannya bergantung pada pilihannya. Analog diskrit dari norma kontinuitas seragam sering digunakan:

terkadang analogi diskrit dari norma integral digunakan.

Contoh. Perkiraan operator dengan operator beda hingga

pada interval terbatas mempunyai orde kedua pada kelas fungsi halus.

Masalah beda hingga mendekati masalah diferensial, dan perkiraannya mempunyai orde, jika persamaan diferensial itu sendiri dan kondisi batas (dan awal) didekati dengan operator beda hingga yang bersesuaian, dan perkiraannya mempunyai urutan.

Kondisi berani

Kondisi berani (dalam sastra Inggris) Kondisi Courant-Friedrichs-Levy , CFL) - kecepatan rambat gangguan dalam masalah perbedaan tidak boleh kurang dari pada masalah diferensial. Jika kondisi ini tidak terpenuhi, maka hasil skema selisih cenderung tidak menyelesaikan persamaan diferensial. Dengan kata lain, dalam satu langkah waktu, partikel tidak boleh “melewati” lebih dari satu sel.

Dalam kasus skema yang koefisiennya tidak bergantung pada penyelesaian persamaan diferensial, kondisi Courant mengikuti stabilitas.

Skema pada jaringan offset

Dalam skema ini, kisi-kisi tempat hasil diberikan dan datanya diimbangi satu sama lain. Misalnya, titik hasil berada di tengah-tengah antara titik data. Dalam beberapa kasus, hal ini memungkinkan penggunaan kondisi batas yang lebih sederhana.

Lihat juga

Tautan

• “Skema perbedaan” - Bab dalam buku wiki dengan topik “Skema perbedaan untuk persamaan hiperbolik”
• Demyanov A.Yu., Chizhikov D.V. Skema perbedaan monotonik hibrid implisit dengan akurasi tingkat kedua
• V.S.Ryabenkiy, A.F.Filippov. Tentang stabilitas persamaan perbedaan. - M.: Gostekhizdat, 1956.
• S.K.Godunov, V.S.Ryabenky. Pengantar teori skema perbedaan. - M.: Fizmatgiz, 1962.
• K.I.Babenko. Dasar-dasar analisis numerik. - M.: Sains, 1986.
• Berezin I.S., Zhidkov N.P. Metode perhitungan, - Edisi apa saja.
• Bakhvalov N.S., Zhidkov N.P., Kobelkov G.M. Metode numerik, - Edisi apa saja.
• G.I.Marchuk. Metode matematika komputasi. - M.: Sains, 1977.

Catatan

Yayasan Wikimedia. 2010.

Lihat apa itu “Skema Perbedaan” di kamus lain:

Sistem persamaan selisih yang mendekati persamaan diferensial dan kondisi tambahan (awal, batas, dll.). Perkiraan masalah diferensial awal R. s. ini adalah salah satu cara untuk memperkirakan diskritisasi masalah aslinya... Ensiklopedia Matematika

perbedaan skema elemen hingga- metode elemen hingga - [A.S. Goldberg. Kamus energi Inggris-Rusia. 2006] Topik energi secara umum Sinonim metode elemen hingga EN jadwal perbedaan volume hingga ...

Skema selisih adalah sistem persamaan aljabar berhingga, yang dikorespondensikan dengan masalah diferensial apa pun yang berisi persamaan diferensial dan kondisi tambahan (misalnya, kondisi batas dan/atau ... ... Wikipedia

skema perhitungan perbedaan hingga berdasarkan volume kontrol- (misalnya perpindahan panas dan massa, konduktivitas termal) [A.S. Goldberg. Kamus energi Inggris-Rusia. 2006] Topik energi secara umum EN jadwal perbedaan hingga berdasarkan volume kendali ... Panduan Penerjemah Teknis

Garis Besar: dokumen grafis; presentasi, gambar, penyajian sesuatu dalam istilah yang paling umum, disederhanakan (misalnya, diagram laporan); perangkat elektronik yang mengandung banyak komponen (rangkaian terpadu). Dokumen grafis... ... Wikipedia

Skema perbedaan dibangun berdasarkan masalah variasional yang berhubungan dengan masalah nilai batas persamaan diferensial. Ide pokok membangun R.v. Dengan. adalah dengan pilihan fungsi koordinat khusus dalam metode Ritz... ... Ensiklopedia Matematika

Metode numerik untuk menyelesaikan metode menyelesaikan persamaan giierbolpch. mengetik berdasarkan algoritma komputasi. Berbagai matematika model dalam banyak kasus mengarah pada persamaan diferensial hiperbolik. jenis. Persamaan tersebut memiliki aialit yang tepat... ... Ensiklopedia Matematika

Cabang matematika komputasi yang mempelajari metode penyelesaian perkiraan persamaan diferensial dengan menggantinya dengan persamaan beda hingga (skema selisih). R.s. t.mempelajari metode untuk membangun skema perbedaan,... ... Ensiklopedia Matematika

Metode numerik untuk menyelesaikan persamaan diferensial parsial adalah metode penyelesaian perkiraan, sehingga penyelesaian masalah diwakili oleh tabel angka. Solusi eksak (berupa rumus eksplisit, deret, dll) K. z. hanya dapat dibangun dalam keadaan langka... Ensiklopedia Matematika

Metode penyelesaian masalah dinamika gas berdasarkan algoritma komputasi. Mari kita perhatikan aspek utama teori metode numerik untuk menyelesaikan masalah dinamika gas, menuliskan persamaan dinamika gas dalam bentuk hukum kekekalan dalam persamaan inersia... ... Ensiklopedia Matematika buku elektronik

Contoh 1. Skema perbedaan persamaan Poisson tipe elips.

Mari kita pertimbangkan konstruksi skema perbedaan untuk masalah nilai batas pertama persamaan tersebut A kamu = f(x,y) pada suatu luas persegi panjang yang sisi-sisinya sejajar sumbu koordinat. Biarkan persegi panjang ini dihubungkan dengan grid seragam dengan langkah-langkah jam x Dan hai .

Masalah nilai batas

dapat ditulis dalam bentuk operator:

Perhatikan bahwa entri ini juga mencakup kondisi batas.

Mengganti operator diferensial dengan operator selisih, kita memperoleh persamaannya

yang mendekati persamaan diferensial asli dengan orde kedua 0(jam 2 + jam 2) akurasi dan beroperasi di semua titik internal wilayah.

Perbedaan analogi kondisi batas akan berbentuk

Perkiraan perbedaan persamaan diferensial bersama dengan analogi perbedaan kondisi batas membentuk skema perbedaan persamaan Poisson.

Dengan analogi masalah nilai batas, skema selisih dapat dituliskan dalam bentuk operator:

dimana dalam L/, persamaan selisih dan syarat batas selisih disertakan:

Persamaan selisih tersebut menghubungkan nilai fungsi grid pada lima titik pembentuk pola perbedaan untuk persamaan ini. Untuk kasus ini, pola ini disebut menyeberang. Kita dapat membayangkan pola lain untuk persamaan ini.

Kita akan memperoleh solusi perkiraan masalah nilai batas diferensial jika kita menentukan nilai fungsi grid di semua node internal domain. Untuk melakukan ini, perlu untuk bersama-sama menyelesaikan sistem persamaan linier aljabar, yang dimensinya sama dengan jumlah simpul internal suatu wilayah. Dalam hal ini, kita berbicara tentang skema perbedaan implisit. Nilai apa pun yang kami minati Uij dapat ditentukan hanya dari solusi seluruh masalah perbedaan.

Mengenai sistem persamaan, kami mencatat dua keadaan.

• 1. Sistem mempunyai dimensi yang sangat tinggi (M - 1) x (N- 1), dan metode tradisional untuk penyelesaian eksak (misalnya, metode Gauss) memerlukan penyelesaian sejumlah operasi aljabar yang sebanding dengan pangkat ketiga dari dimensi sistem.
• 2. Matriks sistem mempunyai banyak elemen nol (matriks lepas). Keadaan ini memungkinkan untuk mengembangkan metode ekonomis untuk solusi perkiraan.

Rumusan masalah perbedaan yang dipertimbangkan adalah tipikal persamaan elips. Dalam dinamika gas, ini adalah bentuk persamaan fungsi aliran atau potensial kecepatan. Pada bagian lain kita akan melihat metode yang efisien untuk menyelesaikan skema perbedaan tersebut.

Beras. 2.8.

PRI M 2. Skema perbedaan persamaan parabola paling sederhana (konduktivitas termal non-stasioner dalam batang dengan satuan panjang).

Pertimbangkan masalah berikut:

Perhatikan bahwa dalam kasus persamaan parabola kita mempunyai daerah terbuka. Ketika membangun skema perbedaan, muncul beberapa pilihan untuk menghubungkan turunan perbedaan dalam ruang dan waktu.

Mari kita integrasikan persamaan tersebut dalam satu langkah waktu:

Bergantung pada rumus kuadratur yang kita gunakan untuk menghitung integral di ruas kanan, kita akan memperoleh skema selisih yang berbeda (Gbr. 2.9).

Dengan menghubungkan turunan perbedaan waktu dengan turunan spasial yang ditentukan P-lapisan waktu, kita dapatkan

'skema perbedaan' yang eksplisit

Hal ini setara dengan perhitungan perkiraan integral pada ruas kanan (2.12), tetapi menggunakan metode persegi panjang kiri.

Beras. 2.9. Grid dan templat untuk persamaan panas: A - area dan jaringan; B- templat skema eksplisit; V- templat skema implisit; G- templat dari keluarga sirkuit enam titik; D- templat diagram

"melompati"

Rumus di atas juga berisi metode penyelesaian persamaan grid:

Nilai fungsi kisi pada lapisan waktu berikutnya

ditentukan melalui nilai gf yang diketahui sebelumnya. Bergerak secara berurutan berlapis-lapis dari kondisi awal milik mereka, 0) = kamu(x), solusinya dapat ditemukan di seluruh domain komputasi. Pola perbedaan untuk skema ini ditunjukkan pada Gambar. 2.9, B.

Memperkirakan integral melalui nilai integran pada lapisan P+1, kami menggunakan templat perbedaan seperti Gambar. 2.9, b, dan analogi selisih persamaan diferensial berbentuk

Untuk mencari nilai fungsi grid pada lapisan waktu berikutnya, dengan menggunakan skema selisih ini, perlu diselesaikan secara bersama-sama persamaan bentuk (2.14) sebanyak node internal yang terletak di P - Lapisan sementara ke-1-1. Dengan mempertimbangkan kondisi batas = / n+1, Mg Г +1 = m n+1, sistem memungkinkan kita untuk membangun solusi pada lapisan waktu berikutnya dengan nilai fungsi grid yang diketahui pada lapisan waktu sebelumnya. Dengan berpindah dari nilai awal berlapis-lapis, yang masing-masingnya perlu menyelesaikan sistem persamaan, dimungkinkan untuk membangun solusi perkiraan di seluruh domain.

Skema perbedaan yang dipertimbangkan adalah sebuah contoh skema perbedaan implisit, ini disebut skema melihat ke depan atau skema yang murni implisit.

Pola perbedaan enam poin menghasilkan serangkaian skema perbedaan, yang mana dua skema sebelumnya merupakan kasus khusus:

Pada sebuah = 0 kami memiliki skema eksplisit, dengan a = saya- implisit dengan muka, dengan A> 0 - implisit. Pada A - 0,5 kita memperoleh yang simetris, yang dikenal luas dalam praktik komputasi Diagram Crank Nicholson.

Skema di atas, tentu saja, tidak menghabiskan seluruh variasi skema perbedaan berdasarkan perkiraan perbedaan operator diferensial. Berikut adalah contoh skema perbedaan eksplisit berdasarkan pemusatan turunan waktu, skema yang menggunakan fungsi grid pada tiga lapisan waktu:

Pola perbedaan menangkap tiga lapisan waktu. Skema ini memiliki perkiraan urutan kedua baik dalam waktu maupun dalam variabel spasial dan bersifat eksplisit. Skema ini memiliki sejumlah kelemahan signifikan, yang sebagian besar dapat dihilangkan dengan penggantian Dan” dalam perkiraan turunan spasial dengan nilai rata-rata pada dua lapisan waktu:

Dengan demikian diperoleh skema tiga lapis yang eksplisit

ditelepon Skema Dufortpe-Frankel, dan tidak adanya nilai fungsi grid di node pusat menjelaskan nama “leapfrog”, yang terkadang digunakan untuk skema semacam ini.

Dengan menggunakan contoh, ditunjukkan bahwa untuk masalah nilai batas yang sama dimungkinkan untuk menulis beberapa skema perbedaan yang berbeda, yaitu. Peneliti memiliki pilihan yang cukup banyak. Kondisi apa yang harus dipenuhi oleh skema perbedaan agar solusi perbedaan sesuai dengan solusi masalah diferensial awal? Masalah ini akan dibahas pada bagian selanjutnya.

konfigurasi node, nilai-nilai fungsi grid yang menentukan bentuk persamaan perbedaan pada titik-titik grid internal (non-batas). Biasanya, dalam gambar dengan gambar templat, titik-titik yang terlibat dalam penghitungan turunan dihubungkan oleh garis.

Skema Courant-Isakson-Ries(KIR), yang terkadang juga dikaitkan dengan nama S.K. Godunov, ternyata ketika , . Urutan perkiraannya adalah. Skema KIR stabil secara kondisional, yaitu. ketika kondisi Courant terpenuhi . Mari kita sajikan persamaan perbedaan untuk skema Courant-Isakson-Ries pada titik internal domain komputasi:

Skema ini, disebut juga skema dengan perbedaan melawan arah angin (dalam literatur Inggris - melawan arah angin), dapat ditulis dalam bentuk

Keuntungannya adalah penghitungan area ketergantungan solusi yang lebih akurat. Jika kita memperkenalkan notasi

maka kedua skema tersebut dapat ditulis dalam bentuk berikut:

(bentuk aliran persamaan selisih);

(di sini istilah dengan perbedaan kedua disorot dengan jelas, yang memberikan stabilitas pada skema);

(persamaan dalam peningkatan terbatas).

Mari kita pertimbangkan juga metode koefisien tidak pasti untuk membuat skema perbedaan, sudut kanan orde ketelitian pertama untuk persamaan transpor

Skema tersebut dapat direpresentasikan dalam bentuk

Skema Courant-Isakson-Rees berkaitan erat dengan metode karakteristik numerik. Mari kita beri gambaran singkat tentang gagasan metode tersebut.

Dua skema terakhir yang diperoleh (dengan tanda kecepatan transfer yang berbeda) dapat diinterpretasikan sebagai berikut. Mari kita buat suatu karakteristik yang melewati simpul (t n + 1, x m), yang nilainya harus ditentukan, dan memotong lapisan t n di titik tersebut . Untuk lebih pastinya, kita asumsikan bahwa laju transfer c adalah positif.

Melakukan interpolasi linier antara node x m - 1 dan x m pada lapisan bawah tepat waktu, kita peroleh

Selanjutnya, kita pindahkan nilai u n (x") sepanjang karakteristik tanpa mengubah ke lapisan atas t n + 1, yaitu kita masukkan . Wajar jika menganggap nilai terakhir sebagai solusi perkiraan persamaan homogen transfer. Pada kasus ini

atau, berpindah dari nomor Courant lagi ke parameter grid,

itu. dengan menggunakan metode lain kita sampai pada skema “sudut kiri” yang sudah diketahui, stabil untuk . Bila titik potong karakteristik yang meninggalkan simpul (t n + 1, x m, dengan lapisan ke-n pada waktunya terletak di sebelah kiri simpul (t n, x m - 1). Maka, untuk mencari penyelesaiannya bukan lagi interpolasi, melainkan ekstrapolasi yang ternyata tidak stabil.

Ketidakstabilan skema "sudut kanan" untuk c > 0 juga terlihat jelas. Untuk membuktikan hal ini, seseorang dapat menggunakan fitur spektral atau kondisi Courant, Friedrichs dan Levy. Alasan serupa dapat dilakukan untuk kasus c< 0 и схемы "правый уголок".

Tidak stabil sirkuit empat titik ternyata kapan , urutan perkiraannya. Persamaan grid untuk skema selisih akan berbentuk sebagai berikut:

Skema Lax-Wendroff terjadi ketika . Urutan perkiraan skema Lax-Wendroff adalah . Skema ini stabil dalam kondisi Courant .

Skema ini dapat diperoleh baik dengan metode koefisien yang tidak dapat ditentukan, atau dengan memperhitungkan suku terdepan dari kesalahan perkiraan secara lebih akurat. Mari kita perhatikan proses derivasi skema Lax-Wendroff secara lebih rinci. Melakukan studi tentang skema perkiraan empat titik sebelumnya (dan studi ini cukup mendasar dan bertujuan untuk memperluas fungsi proyeksi ke grid solusi eksak dari masalah diferensial dalam deret Taylor), kita memperoleh yang utama jangka waktu kesalahannya

Saat menurunkan ekspresi untuk suku utama kesalahan aproksimasi, konsekuensi dari persamaan transpor diferensial asli digunakan

Yang diperoleh dengan membedakan persamaan asli (3.3) terlebih dahulu terhadap waktu t, kemudian terhadap koordinat x dan mengurangkan salah satu relasi yang dihasilkan dari relasi lainnya.

Selanjutnya, penggantian turunan kedua pada suku kedua di ruas kanan dengan ketelitian O(h 2), kita memperoleh skema selisih baru yang mendekati skema aslinya persamaan diferensial dengan presisi . Persamaan grid untuk skema Lax-Wendroff pada node internal grid komputasi adalah

Skema enam poin implisit terjadi pada q = 0; ketika urutan perkiraannya , pada .

Dengan menggunakan templat untuk setiap simpul internal di wilayah solusi, persamaan panas didekati

Dari sini kita menemukan:

Dengan menggunakan kondisi awal dan batas, nilai fungsi grid ditemukan di semua node pada tingkat waktu nol.

Kemudian menggunakan relasi

nilai fungsi ini ditemukan di semua node internal pada level waktu pertama, setelah itu kita menemukan nilai di node batas

Hasilnya, kami menemukan nilai fitur di semua node pada level pertama kali. Setelah ini, dengan menggunakan relasi ini kita menemukan semua nilai lainnya, dll.

Dalam skema selisih yang dipertimbangkan, nilai fungsi yang diinginkan pada tingkat waktu berikutnya ditemukan secara langsung, secara eksplisit menggunakan rumus

Oleh karena itu, skema selisih yang dipertimbangkan dengan menggunakan pola ini disebut skema perbedaan eksplisit . Akurasinya sangat tinggi.

Skema perbedaan ini mudah digunakan, namun memiliki kelemahan yang signifikan. Ternyata skema perbedaannya jelas mempunyai solusi yang stabil hanya jika itu, jika syaratnya terpenuhi :

Skema perbedaan eksplisit stabil secara kondisional . Jika kondisi tersebut tidak terpenuhi, maka kesalahan perhitungan kecil, misalnya terkait dengan pembulatan data komputer, menyebabkan perubahan tajam dalam solusi. Solusinya menjadi tidak dapat digunakan. Kondisi ini menerapkan pembatasan langkah waktu yang sangat ketat, yang mungkin tidak dapat diterima karena peningkatan waktu komputasi yang signifikan untuk menyelesaikan masalah ini.

Pertimbangkan skema perbedaan menggunakan pola yang berbeda

Metode 36

Skema perbedaan implisit untuk persamaan panas.

Mari kita substitusikan ke dalam persamaan konduksi panas:

Relasi ini ditulis untuk setiap node internal pada tingkat waktu dan dilengkapi dengan dua relasi yang menentukan nilai pada node batas. Hasilnya adalah sistem persamaan untuk menentukan nilai fungsi yang tidak diketahui pada tingkat waktu.

Skema penyelesaian masalah tersebut adalah sebagai berikut:

Dengan menggunakan kondisi awal dan kondisi batas, nilai fungsi ditemukan pada tingkat waktu nol. Kemudian, dengan menggunakan relasi dan kondisi batas tersebut, dibangun sistem persamaan aljabar linier untuk mencari nilai fungsi pada tingkat waktu pertama, setelah itu sistem dibangun kembali menggunakan relasi tersebut, dan ditemukan nilainya. pada tingkat kedua kalinya, dll.

Perbedaan dari skema eksplisit- nilai pada level waktu berikutnya tidak dihitung secara langsung menggunakan rumus yang sudah jadi, tetapi ditemukan dengan menyelesaikan sistem persamaan, yaitu. nilai-nilai yang tidak diketahui ditemukan secara implisit dengan menyelesaikan SLAE. Oleh karena itu, skema perbedaan disebut implisit. Berbeda dengan eksplisit, implisit benar-benar stabil.

Topik No.9

Masalah optimasi.

Masalah-masalah ini adalah salah satu masalah terpenting dalam matematika terapan. Maksudnya optimasi memilih opsi terbaik dari semua solusi yang mungkin untuk suatu masalah tertentu. Untuk itu perlu dirumuskan masalah yang dipecahkan secara matematis, memberikan makna kuantitatif pada konsep lebih baik atau lebih buruk. Biasanya, selama proses solusi, perlu untuk menemukan nilai parameter yang dioptimalkan. Parameter ini disebut desain. Dan jumlah parameter desain menentukan dimensi masalah.

Penilaian kuantitatif terhadap solusi dilakukan dengan menggunakan fungsi tertentu tergantung pada parameter desain. Fungsi ini disebut target . Dibangun sedemikian rupa sehingga nilai paling optimal sesuai dengan nilai maksimum (minimum).

- fungsi objektif.

Kasus paling sederhana adalah ketika fungsi tujuan bergantung pada satu parameter dan ditentukan oleh rumus eksplisit. Ada beberapa fungsi target.

Misalnya, ketika merancang sebuah pesawat terbang, penting untuk memastikan keandalan maksimum, bobot dan biaya minimum, dll. Jika demikian, masukkan sistem prioritas . Setiap fungsi tujuan diberi pengali target tertentu, sehingga menghasilkan fungsi tujuan yang digeneralisasi (fungsi trade-off).

Biasanya, solusi optimal dibatasi oleh sejumlah kondisi yang berkaitan dengan fungsi fisik dari masalah tersebut. Kondisi tersebut dapat berupa kesetaraan maupun kesenjangan

Teori dan metode penyelesaian masalah optimasi dengan adanya batasan menjadi bahan penelitian di salah satu cabang matematika terapan - pemrograman matematika.

Jika fungsi tujuan adalah linier terhadap parameter desain dan batasan yang dikenakan pada parameter juga linier, maka masalah pemrograman linier . Mari kita pertimbangkan metode untuk memecahkan masalah optimasi satu dimensi.

Diperlukan untuk mencari nilai di mana fungsi tujuan memiliki nilai maksimum. Jika fungsi tujuan ditentukan secara analitis dan ekspresi turunannya dapat ditemukan, maka solusi optimal akan dicapai pada ujung segmen atau pada titik di mana turunannya hilang. Ini adalah titik-titik kritis dan. Penting untuk menemukan nilai fungsi tujuan di semua titik kritis dan memilih nilai maksimum.

Secara umum, berbagai metode pencarian digunakan untuk mencari solusi. Akibatnya, segmen yang berisi solusi optimal menyempit.

Mari kita lihat beberapa metode pencarian. Mari kita asumsikan bahwa fungsi tujuan pada interval tersebut mempunyai satu maksimum. Dalam hal ini, membagi dengan titik nodal yang banyaknya adalah , fungsi tujuan dihitung pada titik nodal tersebut. Misalkan nilai maksimum fungsi tujuan berada pada titik simpul, maka kita dapat berasumsi bahwa solusi optimal terletak pada interval tersebut. Akibatnya, segmen yang berisi solusi optimal menjadi menyempit. Segmen baru yang dihasilkan dibagi lagi menjadi beberapa bagian, dan seterusnya. Dengan setiap partisi, segmen yang berisi solusi optimal dikurangi dengan satu faktor.

Mari kita asumsikan bahwa langkah-langkah penyempitan telah dilakukan. Kemudian ruas asal dikurangi satu faktor.

Artinya, kita melakukannya saat sedang berjalan (*)

Dalam hal ini, fungsi tujuan dihitung.

Diperlukan untuk mencari nilai sedemikian rupa sehingga diperoleh ekspresi (*) yang paling kecil

sejumlah perhitungan.

Metode 37

Metode setengah pembagian.

Mari pertimbangkan metode pencarian untuk . Disebut metode separuh, karena pada setiap langkah segmen yang mengandung solusi optimal dibelah dua.

Efisiensi pencarian dapat ditingkatkan dengan memilih secara khusus titik-titik di mana fungsi tujuan dihitung pada langkah penyempitan tertentu.

Metode 38

Metode bagian emas.

Salah satu cara yang efektif adalah metode rasio emas. Bagian emas suatu segmen adalah titik dimana kondisinya terpenuhi

Ada dua poin seperti itu: =0,382 +0,618

0,618 +0,382 .

Ruas tersebut dibagi dengan titik-titik dan kemudian ditemukan suatu titik yang fungsi tujuannya maksimum. Hasilnya, ditemukan segmen termodifikasi dengan panjang 0,618( - ).

Salah satu nilai bagian emas untuk segmen yang menyempit sudah diketahui, sehingga pada setiap langkah selanjutnya perlu menghitung fungsi tujuan hanya pada satu titik (titik kedua dari bagian emas).

Metode 39

Metode pendakian (penurunan) koordinat demi koordinat.

Mari kita beralih ke masalah optimasi dalam kasus di mana fungsi tujuan bergantung pada beberapa nilai parameter. Metode pencarian yang paling sederhana adalah metode pendakian (penurunan) koordinat demi koordinat.

Ada tiga metode untuk membangun skema perbedaan pada template tertentu:

· metode pendekatan perbedaan;

· metode integro-interpolasi;

· metode koefisien yang tidak dapat ditentukan.

metode perkiraan perbedaan Kita telah menggunakan (24), (26) saat menyusun skema. Menurut metode ini, setiap turunan yang termasuk dalam persamaan dan kondisi batas diganti dengan beberapa ekspresi perbedaan dengan mempertimbangkan simpul-simpul dari templat tertentu. Metode ini memudahkan pembuatan skema perbedaan dengan pendekatan orde pertama dan kedua, jika koefisien persamaan merupakan fungsi yang cukup halus. Sulit untuk menggeneralisasi pendekatan ini pada sejumlah kasus penting. Misalnya, jika koefisien persamaan terputus-putus, atau seharusnya menggunakan jaring non-persegi panjang dan non-seragam, ketidakpastian muncul dalam konstruksi skema perbedaan.

Menggunakan metode integro-interpolasi atau metode keseimbangan gunakan pertimbangan fisik tambahan, yang bermuara pada penyusunan persamaan kekekalan untuk besaran tertentu. Dalam metode ini, setelah memilih template, area dibagi menjadi beberapa sel. Persamaan diferensial diintegrasikan melalui sel dan, dengan menggunakan rumus analisis vektor, direduksi menjadi bentuk integral yang sesuai dengan hukum integral tertentu. Integral dihitung kira-kira menggunakan salah satu rumus kuadratur dan diperoleh skema selisih.

Mari kita sajikan persamaan konduktivitas termal dengan koefisien konduktivitas termal variabel dalam bentuk: . Untuk memperkirakannya, kami memilih templat yang ditunjukkan pada Gambar. 8, di mana sel yang sesuai disorot dengan garis putus-putus.

Mari kita lakukan integrasi pada sel:

dan perkirakan integral pertama dengan rumus rata-rata, dan integral kedua dengan rumus persegi panjang, lalu

Dalam ekspresi terakhir, kita mengganti turunannya dengan selisih hingga dan, dengan menganggap kisi-kisinya seragam, kita memperoleh skema selisih

Jika k= const, maka skema (35) bertepatan dengan skema implisit (24).

Gambar.8. Templat dan sel interpolasi integro
metode persamaan panas

Metode interpolasi integro paling berguna ketika koefisien persamaannya tidak mulus atau bahkan terputus-putus. Dalam hal ini, beralih ke hukum yang lebih umum - hukum integral - mengembalikan kita ke solusi umum yang lebih tepat.

Mari kita perhatikan contoh penggunaan skema perbedaan (35) untuk menghitung konduktivitas termal suatu medium yang terdiri dari tiga media dengan koefisien konduktivitas termal yang berbeda, yaitu.

(36)

Di mana k 1 , k 2 , k 3, secara umum, adalah bilangan non-negatif yang berbeda. Dalam hal ini, persamaan aslinya dapat ditulis sebagai:

(37)

Untuk menghitung menggunakan skema (35) dengan koefisien konduktivitas termal (36), kita asumsikan bahwa

dan di sebelah kiri X= 0 dan kanan X = A batas menurut (37), kita akan mempertahankan suhu nol, yaitu. Dan .

Listing_No.4 menunjukkan kode program yang menyelesaikan persamaan (36), (37) sesuai dengan skema selisih (35), (38).

Daftar_No.4

%Program untuk menyelesaikan persamaan panas

%(37) dengan koefisien kesenjangan

%konduktivitas termal (36)

global sebuah k1 k2 k3

%tentukan segmen integrasi dan

%tiga nilai koefisien konduktivitas termal

%di tiga area interval integrasi

sebuah=3; k1=0,1; k2=100; k3=10;

%menentukan langkah dalam ruang dan waktu

tau=0,05; h=0,05;

x=0:h:a; N=panjang(x);

%Membangun distribusi suhu awal

jika x(i)<=0.5*a

y(i)=((2*Tm)/a)*x(i);

jika x(i)>0,5*a

y(i)=((2*Tm)/a)*(a-x(i));

%gambar profil suhu awal

%garis merah tebal

plot(x,y,"Warna","merah","Lebar Garis",3);

%hitung koefisien sapuan A(n), B(n)

%C(n): A(n)y2(n+1)+B(n)y2(n)+C(n)y2(n-1)=y(n)

A(n)=-(tau/h^2)*k(x(n)+0,5*h);

B(n)=1+(tau/h^2)*...

(k(x(n)+0,5*t)+k(x(n)-0,5*t));

C(n)=-(tau/h^2)*k(x(n)-0,5*h);

%tentukan kondisi batas kiri

alfa(2)=0; beta(2)=0;

alfa(n+1)=-A(n)/(B(n)+C(n)*alfa(n));

beta(n+1)=(y(n)-C(n)*beta(n))/...

(B(n)+C(n)*alfa(n));

%atur kondisi batas yang tepat

untuk n=(N-1):-1:1

y(n)=alfa(n+1)*y(n+1)+beta(n+1);

%gambar profil suhu saat ini

% menentukan koefisien konduktivitas termal

global sebuah k1 k2 k3

jika (x>=0)&(x<=a/3)

jika (x>a/3)&(x<=(2*a)/3)

jika (x>(2*a)/3)&(x<=a)

Gambar 9 menunjukkan hasil kode program pada Listing_No.4. Profil suhu segitiga awal digambar dengan garis merah tebal. Panah vertikal pada grafik memisahkan area dengan koefisien konduktivitas termal yang berbeda. Menurut kode listing_no.4, koefisien konduktivitas termal berbeda satu sama lain sebanyak tiga kali lipat.

Gambar.9. Penyelesaian persamaan kalor (37) dengan diskontinu
koefisien konduktivitas termal (36)

Metode koefisien tak tentu adalah bahwa kombinasi solusi linier pada titik-titik templat tertentu diambil sebagai skema perbedaan. Koefisien kombinasi linier ditentukan dari kondisi orde maksimum dari sisa yang bersesuaian dalam hal T Dan H.

Jadi, untuk persamaan pada template pada Gambar 8 kita dapat menulis skema berikut dengan koefisien yang belum ditentukan

Menentukan sisa

Mari kita substitusikan (31) ke (40), lalu

(41)

Sebagian besar istilah dalam (41) hilang dalam kondisi tersebut

. (42)

Substitusikan (42) ke (39) kita peroleh skema selisih (24).

Metode koefisien tak tentu juga dapat diterapkan pada kasus-kasus yang lebih kompleks. Misalnya, untuk jaring segitiga, templatnya ditunjukkan pada Gambar 10, Anda bisa mendapatkan skema perbedaan berikut

Gambar 10. Templat jaring segitiga untuk persamaan perbedaan (43)

Mari kita pertimbangkan node tidak beraturan dari skema perbedaan, mis. kondisi batasnya. Untuk persamaan panas kamu = kamu xx simpul batas tidak beraturan N= 0 dan N = N. Jika masalah nilai batas pertama dipertimbangkan

maka mudah untuk menuliskan kondisi perbedaan yang sesuai

yang dilakukan secara akurat, karena sisa bagi mereka adalah nol.

Yang lebih kompleks adalah kasus masalah nilai batas kedua, ketika kondisi batas mengandung turunan terhadap X. Misalnya, ketika menentukan aliran panas pada tepinya, kondisi batasnya berbentuk sebagai berikut:

Turunan pada (44) dapat didekati dengan selisih hingga kanan (kiri):

Perbedaan persamaan selisih (45) mudah diperkirakan:

(46)

Jadi, menurut (46), ketidaksesuaian kondisi batas memiliki keakuratan urutan pertama H, sedangkan pada titik reguler urutan keakuratannya berada di urutan kedua H, yaitu. ketika memilih perkiraan kondisi batas menggunakan rumus (45), terjadi kehilangan akurasi.

Untuk meningkatkan keakuratan kondisi batas, pertimbangkan metode titik fiktif. Mari kita perkenalkan dua titik fiktif di luar segmen: , dan tuliskan dalam titik-titik N= 0 dan N = N skema perbedaan eksplisit (26), lalu

Kami memperkirakan kondisi batas kiri dan kanan menggunakan perbedaan pusat, yaitu.

Tidak termasuk titik fiktif dan nilai fungsi di dalamnya dari (47), (48), kami menemukan kondisi batas akurasi orde kedua di H:

(49)

Syarat batas (49) bersifat eksplisit, karena hanya berisi satu nilai pada lapisan berikutnya.

Selain metode titik fiktif, ada metode lain untuk mengurangi kesenjangan; metode ini lebih universal, namun kurang visual. Mari kita terurai kamu(T,X 1) di sekitarnya X 0 lalu

Menurut (44), , dan dari persamaan konduksi panas kita temukan . Mengganti perkiraan ini ke dalam ekspansi Taylor, kami menemukan

Dengan melakukan substitusi pada (50), kita memperoleh kondisi batas kiri (49).

Berdasarkan prosedur di atas, peningkatan akurasi dalam memperkirakan kondisi batas dapat dicapai.

Perkiraan

Biarlah luasnya diberikan G variabel X = (X 1 ,X 2 ,…,xp) dengan batas G dan masalah penyelesaian persamaan dengan kondisi batas yang benar diajukan:

Au(X) - F(X) = 0, X Î G; (51)

Ru(X) - M(X) = 0, X tentang G. (52)

Ayo masuk ke area tersebut G+ G kotak dengan langkah-langkah H, yang berisi node reguler (internal). w h dan node (perbatasan) tidak beraturan g h.

Mari kita masukkan (51), (52) ke analogi perbedaan yang sesuai

A h y h(X) - jh(X) = 0, X Î w h; (51¢)

R h y h(X) - c h(X) = 0, X Î g h. (52¢)

Kedekatan skema selisih (51¢), (52¢) dengan masalah awal (51), (52) ditentukan oleh nilai residu:

Rangkaian selisih (51¢), (52¢) perkiraan masalah (51), (52), kapan

perkiraan memiliki P pesanan ke- kapan

Mari kita beri beberapa komentar mengenai pilihan norma. Untuk mempermudah, kita akan mempertimbangkan kasus satu dimensi, yaitu. G = [A,B].

Anda dapat menggunakan Chebyshev atau norma lokal

,

atau Hilbert berarti persegi:

.

Seringkali dibangun terkait atau dikaitkan dengan suatu operator A standar energi. Misalnya,

Pilihan norma ditentukan oleh dua pertimbangan yang berlawanan. Di satu sisi, diinginkan adanya solusi perbedaan kamu mendekati solusi tepat dalam norma© terkuat. Misalnya, dalam masalah yang melibatkan penghancuran struktur, kecilnya deformasi tidak menjamin integritas struktur, tetapi kecilnya deformasi normal menjamin integritas struktur. Di sisi lain, semakin lemah normanya, semakin mudah untuk membangun skema perbedaan dan membuktikan konvergensinya.

Fungsi kamu h, jh, c h, termasuk dalam (51¢), (52¢), didefinisikan pada grid, jadi bagi mereka perlu untuk menentukan norma grid yang sesuai, dan . Biasanya mereka diperkenalkan agar masuk ke dalam norma yang dipilih, dan kapan H® 0. Ekspresi berikut dipilih sebagai analogi perbedaan dari norma Chebyshev dan Hilbert:

atau analog dekat.

Keberlanjutan

Yang kami maksud dengan stabilitas (ketidakstabilan) skema perbedaan adalah bahwa kesalahan kecil yang timbul selama proses perhitungan (atau diperkenalkan dengan input data) berkurang (meningkat) dalam perhitungan selanjutnya.

Mari kita perhatikan contoh skema perbedaan tidak stabil untuk masalah persamaan diferensial Cauchy kamu¢ = sebuah kamu. Mari kita pilih skema perbedaan keluarga satu parameter berikut:

. (53)

Menyelidiki pertumbuhan kesalahan dy n data awal persamaan (53). Karena persamaan (53) linier, kesalahannya dy n memenuhi persamaan yang sama (53). Mari kita pelajari jenis kesalahan khusus dy n = aku n. Mari kita substitusikan representasi ini ke (53).

Penyelesaian persamaan kuadrat (54) di H® 0 memberikan estimasi akar berikut ini

Dari pendugaan akar-akar pada (55) maka untuk S < ½ второй корень |aku 2 | > 1, yaitu dalam satu langkah kesalahannya meningkat beberapa kali lipat. Mari kita periksa.

Listing_No.5 menunjukkan kode program yang menggambarkan perhitungan untuk kondisi tidak stabil S= skema 0,25 (53) dan menurut skema stabil di S= 0,75. Gangguan kecil dipilih pada data awal. Selanjutnya dilakukan serangkaian perhitungan dengan nilai grid step yang semakin menurun H. Gambar 11 menunjukkan grafik akhir ketergantungan nilai gangguan pada data awal di ujung kanan segmen integrasi tergantung pada langkah grid. Terlihat jelas betapa perbedaan perhitungan skema tidak stabil dan stabil satu sama lain. Dengan menggunakan program ini Anda dapat memverifikasi nilai ambang batas parameter S= 0,5: pada S < 0,5 схема неустойчива, при S³ 0,5 - stabil.

Daftar_No.5

% Program perhitungan untuk skema tidak stabil di

%sigma=0,25 dan menurut skema stabil pada sigma=0,75

%membersihkan ruang kerja

%tentukan konstanta persamaan u"=alpha*u

%tentukan nilai sigma=0,25; 0,75

sigm=0,25:0,5:0,75;

untuk s=1:panjang(sigm)

%menentukan nilai awal langkah grid

x=0:j:1; N=panjang(x);

%menentukan gangguan pada data awal

hari(1)=1e-6; hari(2)=1e-6;

%kita melakukan perhitungan gangguan awal

% data di ujung kanan segmen integrasi

dy(n+1)=(2+(alfa*h-1)/sigma)*dy(n)+...

(1/sigma-1)*dy(n-1);

%ingat gangguan di ujung kanan dan

%jarak kisi

deltay(i)=dy(N);

%gambarlah grafik ketergantungan gangguan pada

% batas kanan dari langkah grid

plot(langkah,delta);

Gambar 11. Grafik ketergantungan gangguan bila dihitung menurut
diagram (53) pada batas kanan langkah grid H

Skema perbedaan(51¢), (52¢) stabil, jika penyelesaian sistem persamaan beda secara kontinyu bergantung pada data masukan J, C dan ketergantungan ini seragam terhadap langkah jaringan. Mari kita perjelas ketergantungan yang berkelanjutan. Artinya bagi siapa pun e> 0 ada seperti itu D(e), independen dari H, Apa

, (56)

Jika skema selisih (51¢), (52¢) linier, maka solusi selisih bergantung linier pada data masukan. Dalam hal ini kita dapat berasumsi demikian D(e) = e/(M + M 1), dimana M, M 1 - beberapa besaran non-negatif yang tidak bergantung pada H. Akibatnya, kondisi stabilitas skema beda linier dapat ditulis sebagai:

Ketergantungan berkelanjutan dari solusi perbedaan J ditelepon stabilitas di sisi kanan, dan dari C - stabilitas menurut data batas.

Kedepannya akan kami pertimbangkan skema perbedaan dua lapis, yaitu. skema seperti itu yang berisi satu lapisan yang diketahui dan satu lapisan baru yang tidak diketahui.

Skema perbedaan dua lapis disebut stabil secara seragam berdasarkan data awal, jika saat memilih data awal dari lapisan mana pun T * (T 0 £ T * < T) skema perbedaannya stabil terhadap mereka, dan stabilitasnya seragam terhadapnya T*. Untuk skema linier, kondisi kestabilan seragam dapat dituliskan dalam bentuk

dimana konstanta K tidak bergantung pada T* Dan H, - solusi skema perbedaan Ah y = J dengan data awal dan dengan sisi kanan yang sama.

Tanda yang cukup untuk stabilitas seragam. Untuk kestabilan yang seragam menurut data awal, cukup untuk semua M dilakukan

Bukti. Kondisi (60) artinya jika terjadi kesalahan pada beberapa lapisan mati, maka saat berpindah ke lapisan berikutnya norma gangguan || mati|| meningkat paling banyak (1 + t) £ e C t sekali. Menurut (59), ketika berpindah dari lapisan T* per lapisan T diperlukan M = (T - T *)/T langkah waktu, yaitu kesalahannya bertambah tidak lebih dari . Sebagai hasilnya, kita punya

yang menurut definisi pada (59) berarti kestabilan seragam menurut data awal.

Dalil. Biarkan skema perbedaan dua lapis Ah y = J stabil secara seragam terhadap data awal dan sedemikian rupa sehingga jika ada dua solusi yang berbeda A h y k = jk sama pada beberapa lapisan, mis. , maka lapisan berikutnya memenuhi relasi tersebut

Di mana A= konstanta. Kemudian skema selisihnya stabil di sisi kanan.

Bukti. Selain solusinya kamu Mari kita perhatikan solusi yang berhubungan dengan ruas kanan yang terganggu. Berikut ini kita akan berasumsi bahwa. Hal ini dapat diasumsikan, karena Stabilitas di sisi kanan dipelajari.