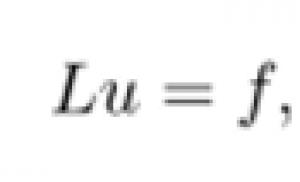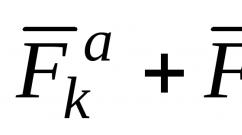Seri fungsional. Deret Fungsional, Daerah Konvergensi, Konvergensi Seragam, Tanda Weierstrass, Sifat-sifat Deret Fungsi yang Konvergen Seragam, Konvergensi Seragam Deret Fungsi dan Sifat-sifatnya

Daerah Konvergensi Deret fungsional adalah deret yang anggota-anggotanya merupakan fungsi/didefinisikan pada himpunan E tertentu pada sumbu bilangan. Misalnya suku-suku suatu deret didefinisikan pada suatu interval, dan suku-suku suatu deret didefinisikan pada suatu interval. Suatu deret fungsional (1) dikatakan konvergen di titik Ho€E jika konvergen SERI FUNGSIONAL Daerah konvergen Seragam Konvergensi Tes Weierstrass Sifat-sifat deret fungsional konvergen seragam Deret numerik Jika deret (1) konvergen di setiap titik x himpunan D C E dan divergen di setiap titik yang bukan himpunan D, maka deret tersebut dikatakan konvergen di himpunan tersebut D, dan D disebut daerah konvergensi deret tersebut. Suatu deret (1) dikatakan konvergen mutlak pada himpunan D jika deret tersebut konvergen pada himpunan tersebut.Dalam kasus konvergensi suatu deret (1) pada himpunan D, jumlah S-nya merupakan suatu fungsi yang terdefinisi pada D. Daerah konvergensi beberapa deret fungsional dapat dicari dengan menggunakan kriteria cukup yang diketahui yang ditetapkan untuk deret dengan suku positif, misalnya uji Dapambert, uji Cauchy. Contoh 1. Tentukan daerah konvergensi deret M Karena deret bilangan konvergen pada p > 1 dan divergen pada p ^ 1, maka dengan asumsi p - Igx, kita memperoleh deret ini. yang akan konvergen di Igx > T yaitu. jika x > 10, dan menyimpang ketika Igx ^ 1, mis. pada 0< х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > Baris 0 divergen, karena A =. Divergensi deret di x = 0 terlihat jelas. Contoh 3. Tentukan daerah konvergensi suatu deret Suku-suku deret tertentu terdefinisi dan kontinu pada himpunan. Menggunakan kriteria Kosh dan, kami menemukan apa pun. Akibatnya, deret tersebut divergen untuk semua nilai x. Mari kita nyatakan dengan Sn(x) jumlah parsial ke-n dari deret fungsional (1). Jika deret ini konvergen pada himpunan D dan jumlahnya sama dengan 5(g), maka deret tersebut dapat dinyatakan dalam bentuk dimana adalah jumlah deret yang konvergen pada himpunan D yang disebut sisa ke-n deret fungsional ( 1). Untuk semua nilai x € D relasinya dan karenanya berlaku. yaitu, sisa Rn(x) suatu deret konvergen cenderung nol sebesar n oo, berapa pun x 6 D. Konvergensi seragam Di antara semua deret fungsional yang konvergen, yang disebut deret konvergen seragam memainkan peranan penting. Misalkan diberikan suatu deret fungsi yang konvergen pada himpunan D yang jumlahnya sama dengan S(x). Mari kita ambil Definisi jumlah parsial ke-n. Deret Fungsional SERI FUNGSIONAL Daerah asal konvergensi Konvergensi seragam Uji Weierstrass Sifat-sifat deret fungsional konvergen seragam dikatakan konvergen seragam pada himpunan PS1) jika untuk sembarang bilangan e > O terdapat bilangan Γ > O sehingga pertidaksamaan berlaku untuk semua bilangan n > N dan untuk semua x dari himpunan fI. Komentar. Di sini bilangan N sama untuk semua x € Yu, yaitu. tidak bergantung pada z, tetapi bergantung pada pilihan bilangan e, maka kita tulis N = N(e). Konvergensi seragam deret fungsi £ /n(®) terhadap fungsi S(x) pada himpunan ft sering dinotasikan sebagai berikut: Definisi konvergensi seragam deret /n(x) pada himpunan ft dapat ditulis lebih singkat menggunakan simbol logika: Mari kita jelaskan secara geometris pengertian rentang fungsi konvergensi seragam. Mari kita ambil segmen [a, 6] sebagai himpunan ft dan buat grafik fungsinya. Pertidaksamaan |, yang berlaku untuk bilangan n > N dan untuk semua a; G [a, b], dapat dituliskan dalam bentuk berikut, Pertidaksamaan yang diperoleh menunjukkan bahwa grafik seluruh fungsi y = 5n(x) dengan bilangan n > N seluruhnya berada dalam pita £ yang dibatasi oleh kurva y = S(x) - e dan y = 5(g) + e (Gbr. 1). Contoh 1 konvergen seragam pada interval Deret ini bertanda bolak-balik, memenuhi syarat kriteria Leibniz untuk sembarang x € [-1,1] dan, oleh karena itu, konvergen pada interval (-1,1). Misalkan S(x ) adalah jumlahnya, dan Sn (x) adalah jumlah parsialnya yang ke-n. Sisa deret yang nilai absolutnya tidak melebihi nilai absolut suku pertamanya: dan karena Mari kita ambil sembarang e, maka pertidaksamaan | akan terpenuhi jika. Dari sini kita menemukan bahwa n > \. Jika kita mengambil suatu bilangan (di sini [a] melambangkan bilangan bulat terbesar tidak melebihi a), maka pertidaksamaan | e akan berlaku untuk semua nomor n > N dan untuk semua x € [-1,1). Artinya deret ini konvergen seragam pada interval [-1,1). I. Tidak semua deret fungsi yang konvergen pada himpunan D konvergen seragam pada Contoh 2. Mari kita tunjukkan bahwa deret tersebut konvergen pada suatu interval, tetapi tidak seragam. 4 Mari kita hitung jumlah parsial ke-n £„(*) dari deret tersebut. Kita mempunyai Dimana deret ini konvergen pada ruas tersebut dan jumlahnya jika Nilai mutlak selisih S(x) - 5„(x) (sisa deret tersebut) adalah sama. Mari kita ambil nomor e sedemikian rupa. Misalkan Kita menyelesaikan pertidaksamaan terhadap n. Kita mempunyai, dari mana (karena, dan bila dibagi dengan Inx, tanda pertidaksamaan berubah menjadi kebalikannya). Ketimpangan akan terpenuhi ketika. Oleh karena itu, terdapat suatu bilangan N(e) yang tidak bergantung pada x sehingga pertidaksamaan terpenuhi untuk setiap) untuk semua x dari ruas tersebut sekaligus. , tidak ada. Jika kita mengganti ruas 0 dengan ruas yang lebih kecil, di mana, maka pada ruas terakhir deret ini akan konvergen secara seragam ke fungsi S0. Faktanya, untuk, dan karena itu untuk semua x sekaligus §3. Uji Weierstrass Uji yang cukup untuk konvergensi seragam suatu deret fungsional diberikan oleh teorema Weierstrass. Teorema 1 (uji Weierstrass). Misalkan untuk semua x dari himpunan Q suku-suku deret fungsional yang nilai absolutnya tidak melebihi suku-suku yang bersesuaian dari deret bilangan konvergen P = 1 dengan suku-suku positif, yaitu untuk semua x € Q. Maka deret fungsional (1 ) pada himpunan P konvergen secara mutlak dan seragam. Dan Tek karena, menurut kondisi teorema, suku-suku deret (1) memenuhi kondisi (3) pada seluruh himpunan Q, maka sebagai perbandingan deret 2 \fn(x)\ konvergen untuk sembarang x € I, dan , akibatnya deret (1) konvergen mutlak di P. Mari kita buktikan konvergensi seragam deret (1). Misalkan Sn(x) dan an masing-masing menyatakan jumlah parsial dari deret (1) dan (2). Kita ambil sembarang bilangan (yang kecil sembarang) e > 0. Kemudian dari konvergensi deret bilangan (2) mengikuti adanya bilangan N = N(e) sehingga, oleh karena itu, -e untuk semua bilangan n > N (e) dan untuk semua xbP , mis. deret (1) konvergen seragam pada himpunan P. Catatan. Deret bilangan (2) sering disebut mayor, atau mayor, untuk deret fungsional (1). Contoh 1. Periksa deret tersebut untuk mengetahui kekonvergenan seragam.Pertidaksamaan berlaku untuk semua deret tersebut. dan untuk semua orang. Deret bilangan tersebut konvergen. Berdasarkan kriteria Weierstrass, deret fungsional yang dipertimbangkan konvergen secara mutlak dan seragam pada seluruh sumbu. Contoh 2. Periksa kekonvergenan seragam dari deret tersebut Suku-suku deret tersebut terdefinisi dan kontinu pada interval [-2,2|. Karena pada interval [-2,2) untuk sembarang bilangan asli n, maka pertidaksamaan berlaku. Karena deret bilangan konvergen, maka menurut kriteria Weierstrass, deret fungsional asli konvergen secara mutlak dan seragam pada segmen tersebut. Komentar. Deret fungsional (1) dapat konvergen secara seragam pada himpunan Piv jika tidak ada deret mayor numerik (2), yaitu kriteria Weierstrass hanya merupakan kriteria yang cukup untuk konvergensi seragam, tetapi tidak diperlukan. Contoh. Seperti yang ditunjukkan di atas (contoh), deret tersebut konvergen secara seragam pada segmen 1-1,1]. Namun untuk itu tidak ada deret bilangan konvergen mayor (2). Faktanya, untuk semua n alami dan untuk semua x € [-1,1) pertidaksamaan terpenuhi dan kesetaraan tercapai ketika. Oleh karena itu, anggota-anggota deret mayor yang diinginkan (2) tentu harus memenuhi syarat tetapi deret bilangan SERI FUNGSIONAL Luas konvergensi Konvergensi seragam Uji Weierstrass Sifat-sifat deret fungsional yang konvergen seragam divergen. Artinya rangkaian £op juga akan berbeda. Sifat-sifat Deret Fungsional Konvergen Seragam Deret fungsi konvergen seragam mempunyai sejumlah sifat penting. Teorema 2. Jika semua suku suatu deret yang konvergen seragam pada interval [a, b] dikalikan dengan fungsi yang sama d(x) yang dibatasi pada [a, 6], maka deret fungsional yang dihasilkan akan konvergen seragam. Misalkan pada interval [a, b\ deret £ fn(x) konvergen seragam ke fungsi 5(x), dan fungsi d(x) dibatasi, yaitu terdapat konstanta C > 0 sehingga menurut definisi konvergensi seragam deret tersebut untuk sembarang bilangan e > 0 terdapat bilangan N sehingga untuk semua n > N dan untuk semua x € [a, b], pertidaksamaan terpenuhi jika 5n(ar) adalah jumlah parsial dari deret tersebut seri yang sedang dipertimbangkan. Oleh karena itu, kami akan menyediakannya untuk semua orang. deret tersebut konvergen seragam pada [a, b| ke fungsi Teorema 3. Misalkan semua suku fn(x) dari deret fungsional kontinu dan deret tersebut konvergen seragam pada interval [a, b\. Maka jumlah S(x) deret tersebut kontinu pada interval tersebut. M Mari kita ambil dua titik sembarang ig + Ax pada ruas [o, b]. Karena deret ini konvergen seragam pada interval [a, b], maka untuk sembarang bilangan e > O terdapat bilangan N = N(e) sehingga untuk semua i > N pertidaksamaan terpenuhi dimana 5„(g) adalah jumlah parsial deret fn(x). Jumlah parsial 5n(x) ini kontinu pada interval [a, 6] sebagai jumlah dari sejumlah fungsi berhingga fn(x) kontinu pada [a, 6]. Oleh karena itu, untuk bilangan tetap no > N(e) dan bilangan tertentu e, terdapat bilangan 6 = 6(e) > 0 sehingga untuk kenaikan Ax yang memenuhi kondisi |, pertidaksamaan akan berlaku: Kenaikan AS dari jumlah S(x) dapat direpresentasikan dalam bentuk berikut: dimana. Dengan memperhitungkan pertidaksamaan (1) dan (2), untuk pertambahan Ax yang memenuhi syarat |, kita peroleh Artinya jumlah Enam) kontinu di titik x. Karena x adalah titik sembarang pada ruas [a, 6], maka 5(x) kontinu di |a, 6|. Komentar. Suatu deret fungsional yang suku-sukunya kontinu pada interval [a, 6), tetapi konvergen tidak beraturan pada (a, 6], dapat mempunyai fungsi diskontinyu sebagai penjumlahan.Contoh 1. Perhatikan deret fungsional pada interval |0,1 ). Mari kita hitung jumlah parsialnya, sehingga segmen tersebut terputus-putus, meskipun suku-suku deret tersebut kontinu pada segmen tersebut. Berdasarkan teorema yang telah terbukti, deret ini tidak konvergen seragam pada intervalnya. Contoh 2. Perhatikan deret Seperti yang ditunjukkan di atas, deret ini konvergen di , deret tersebut akan konvergen secara seragam menurut uji Weierstrass, karena 1 dan deret bilangan tersebut konvergen. Oleh karena itu, untuk sembarang x > 1, jumlah deret tersebut kontinu. Komentar. Fungsi tersebut disebut fungsi Riemann (fungsi ini berperan besar dalam teori bilangan). Teorema 4 (tentang integrasi suku demi suku dari suatu deret fungsional). Misalkan semua suku fn(x) dari deret tersebut kontinu dan deret tersebut konvergen secara seragam pada interval [a, b] ke fungsi S(x). Maka persamaannya berlaku: Karena kontinuitas fungsi f„(x) dan konvergensi seragam deret ini pada interval [a, 6], jumlah 5(x) kontinu dan, oleh karena itu, dapat diintegralkan pada . Mari kita perhatikan perbedaannya Dari konvergensi seragam deret pada [o, b] maka untuk sembarang e > 0 terdapat bilangan N(e) > 0 sehingga untuk semua bilangan n > N(e) dan untuk semua bilangan x € [a, 6] pertidaksamaan terpenuhi Jika deret fn(0 tidak konvergen seragam, maka secara umum deret tersebut tidak dapat diintegrasikan suku demi suku, yaitu Teorema 5 (diferensiasi suku demi suku suatu deret fungsional) Misalkan semua suku pada deret konvergen 00 mempunyai turunan kontinu dan deret yang terdiri dari turunan-turunan tersebut konvergen beraturan pada interval [a,b], maka pada titik mana pun persamaannya benar, yaitu deret ini dapat dibedakan sukunya dengan suku M Mari kita ambil dua titik mana saja, maka, berdasarkan Teorema 4, kita peroleh Fungsi o-(x) kontinu sebagai jumlah dari serangkaian fungsi kontinu yang konvergen seragam. Oleh karena itu, dengan membedakan persamaan kita peroleh Latihan Temukan area konvergensi deret fungsional ini: Dengan menggunakan uji Weierstrass, buktikan konvergensi seragam deret fungsional ini pada interval yang ditunjukkan:

Rentang fungsional disebut ekspresi tertulis formal

kamu1 (X) + kamu 2 (X) + kamu 3 (X) + ... + kamu N( X) + ... , (1)

Di mana kamu1 (X), kamu 2 (X), kamu 3 (X), ..., kamu N( X), ... - urutan fungsi dari variabel bebas X.

Notasi singkat deret fungsional dengan sigma: .

Contoh deret fungsional antara lain :

(2)

(3)

Memberikan variabel independen X beberapa nilai X0 dan mensubstitusikannya ke dalam deret fungsional (1), kita memperoleh deret numerik

kamu1 (X 0 ) + kamu 2 (X 0 ) + kamu 3 (X 0 ) + ... + kamu N( X 0 ) + ...

Jika deret bilangan yang dihasilkan konvergen, maka deret fungsional (1) dikatakan konvergen X = X0 ; jika divergen maka yang dikatakan deret (1) divergen pada X = X0 .

Contoh 1. Selidiki kekonvergenan suatu deret fungsional(2) pada nilai X= 1 dan X = - 1 .
Larutan. Pada X= 1 kita mendapatkan deret angka

yang konvergen menurut kriteria Leibniz. Pada X= - 1 kita mendapatkan deret angka

,

yang divergen sebagai hasil kali deret harmonik divergen sebesar – 1. Jadi, deret (2) konvergen di X= 1 dan divergen di X = - 1 .

Jika pemeriksaan konvergensi deret fungsional (1) dilakukan terhadap semua nilai variabel bebas dari domain definisi anggotanya, maka titik-titik domain tersebut akan dibagi menjadi dua himpunan: untuk nilai-nilai X, diambil salah satunya, deret (1) konvergen, dan deret lainnya divergen.

Himpunan nilai variabel bebas di mana deret fungsional bertemu disebut nya daerah konvergensi .

Contoh 2. Temukan luas konvergensi deret fungsional

Larutan. Suku-suku deret tersebut didefinisikan pada seluruh garis bilangan dan membentuk barisan geometri yang penyebutnya Q= dosa X. Oleh karena itu deret tersebut konvergen jika

dan menyimpang jika

(nilai tidak mungkin). Tapi untuk nilai-nilai dan untuk nilai-nilai lainnya X. Oleh karena itu, deret tersebut konvergen untuk semua nilai X, kecuali . Daerah konvergensinya adalah seluruh garis bilangan, kecuali titik-titik tersebut.

Contoh 3. Temukan luas konvergensi deret fungsional

Larutan. Suku-suku deret tersebut membentuk barisan geometri dengan penyebutnya Q=dalam X. Oleh karena itu, deret tersebut konvergen jika , atau , dari mana . Ini adalah wilayah konvergensi deret ini.

Contoh 4. Selidiki kekonvergenan suatu deret fungsional

Larutan. Mari kita ambil nilai arbitrer. Dengan nilai ini kita mendapatkan deret angka

(*)

Mari kita cari limit suku persekutuannya

Akibatnya, deret (*) menyimpang untuk dipilih secara sewenang-wenang, yaitu. pada nilai berapa pun X. Daerah konvergensinya merupakan himpunan kosong.

Konvergensi seragam suatu deret fungsional dan sifat-sifatnya

Mari beralih ke konsepnya konvergensi seragam deret fungsional . Membiarkan S(X) adalah jumlah deret ini, dan SN( X) - jumlah N anggota pertama dari seri ini. Rentang fungsional kamu1 (X) + kamu 2 (X) + kamu 3 (X) + ... + kamu N( X) + ... disebut konvergen seragam pada interval [ A, B] , jika untuk bilangan kecil apa pun ε > 0 ada nomor seperti itu N itu di depan semua orang N ≥ N ketimpangan akan terpenuhi

|S(X) − S N( X)| < ε

untuk siapa pun X dari segmen [ A, B] .

Sifat-sifat di atas dapat diilustrasikan secara geometris sebagai berikut.

Perhatikan grafik fungsinya kamu = S(X) . Mari kita buat strip dengan lebar 2 di sekeliling kurva ini ε N, yaitu, kita akan membuat kurva kamu = S(X) + ε N Dan kamu = S(X) − ε N(pada gambar di bawah warnanya hijau).

Lalu untuk apa pun ε N grafik suatu fungsi SN( X) akan terletak seluruhnya pada jalur yang ditinjau. Strip yang sama akan berisi grafik dari semua jumlah parsial berikutnya.

Deret fungsional konvergen apa pun yang tidak mempunyai sifat seperti dijelaskan di atas adalah deret fungsional konvergen tak beraturan.

Mari kita pertimbangkan properti lain dari deret fungsional yang konvergen seragam:

jumlah deret fungsi kontinu yang konvergen seragam pada interval tertentu [ A, B] , terdapat fungsi kontinu pada interval ini.

Contoh 5. Tentukan apakah jumlah suatu deret fungsional kontinu

Larutan. Mari kita cari jumlahnya N anggota pertama dari seri ini:

Jika X> 0, lalu

,

Jika X < 0 , то

Jika X= 0, maka

Dan maka dari itu .

Penelitian kami menunjukkan bahwa jumlah deret ini merupakan fungsi diskontinu. Grafiknya ditunjukkan pada gambar di bawah ini.

Uji Weierstrass untuk konvergensi seragam deret fungsional

Kami mendekati kriteria Weierstrass melalui konsep mayorizabilitas deret fungsional . Rentang fungsional

kamu1 (X) + kamu 2 (X) + kamu 3 (X) + ... + kamu N( X) + ...

Lukhov Yu.P. Catatan kuliah tentang matematika tingkat tinggi. Kuliah No.42 5

Kuliah 42

SUBJEK: Seri fungsional

Rencana.

1. Seri fungsional. Wilayah konvergensi.
2. Konvergensi seragam. Tanda Weierstrass.
3. Sifat-sifat deret konvergen beraturan: kontinuitas jumlah deret, integrasi dan diferensiasi suku demi suku.
4. Seri kekuatan. teorema Habel. Daerah konvergensi deret pangkat. Radius konvergensi.
5. Sifat dasar deret pangkat: konvergensi seragam, kontinuitas, dan diferensiasi jumlah yang tak terhingga. Integrasi istilah demi istilah dan diferensiasi rangkaian kekuasaan.

Seri fungsional. Wilayah konvergensi

Definisi 40.1. Jumlah fungsi yang tak terbatas

kamu 1 (x) + kamu 2 (x) +…+ kamu n (x) +…, (40.1)

dimana u n (x) = f (x, n), disebut rentang fungsional.

Jika Anda menentukan nilai numerik tertentu X , deret (40.1) akan berubah menjadi deret angka, dan bergantung pada pilihan nilainya X deret tersebut dapat konvergen atau divergen. Hanya deret konvergen yang memiliki nilai praktis, sehingga penting untuk menentukan nilai tersebut X , yang deret fungsionalnya menjadi deret bilangan konvergen.

Definisi 40.2. Beragam arti X , jika disubstitusikan ke dalam deret fungsional (40.1), diperoleh deret numerik konvergen, disebutdaerah konvergensirentang fungsional.

Definisi 40.3. Fungsi s(x), didefinisikan di daerah konvergensi deret tersebut, yang untuk setiap nilai X dari daerah konvergensi sama dengan jumlah deret numerik bersesuaian yang diperoleh dari (40.1) untuk nilai tertentu x dipanggil jumlah deret fungsional.

Contoh. Mari kita cari daerah konvergensi dan jumlah deret fungsionalnya

1 + x + x² +…+ x n +…

Kapan | X | ≥ 1 oleh karena itu deret bilangan yang bersesuaian berbeda. Jika

| X | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

Oleh karena itu, jangkauan konvergensi deret tersebut adalah interval (-1, 1), dan jumlahnya memiliki bentuk yang ditunjukkan.

Komentar . Sama seperti deret bilangan, Anda dapat memperkenalkan konsep jumlah parsial deret fungsional:

s n = 1 + x + x² +…+ x n

dan sisa deretnya: r n = s s n .

Konvergensi seragam suatu deret fungsional

Mari kita definisikan dulu konsep konvergensi seragam suatu barisan bilangan.

Definisi 40.4. Urutan fungsional fn(x) dipanggil konvergen secara seragam ke fungsi tersebut f di himpunan X jika dan

Catatan 1. Konvergensi biasa suatu barisan fungsional dan konvergensi seragam akan dilambangkan dengan .

Catatan 2 . Mari kita perhatikan sekali lagi perbedaan mendasar antara konvergensi seragam dan konvergensi biasa: dalam kasus konvergensi biasa, untuk nilai ε yang dipilih, untuk masing-masing nilai terdapat nomormu N, untuk itu di n>N ketimpangan berlaku:

Dalam hal ini, mungkin saja untuk ε tertentu adalah bilangan umum N, memastikan terpenuhinya kesenjangan ini bagi siapa pun X , mustahil. Dalam kasus konvergensi seragam, bilangan tersebut N, umum untuk semua x, ada.

Sekarang mari kita definisikan konsep konvergensi seragam suatu deret fungsional. Karena setiap deret bersesuaian dengan barisan jumlah parsialnya, konvergensi seragam deret tersebut ditentukan melalui konvergensi seragam barisan ini:

Definisi 40.5. Deret fungsional disebutkonvergen seragam di himpunan X, jika di X barisan jumlah parsialnya konvergen secara seragam.

Tanda Weierstrass

Teorema 40.1. Jika suatu deret bilangan konvergen untuk semua orang dan semua orang n = 1, 2,... pertidaksamaan terpenuhi kemudian deret-deret tersebut konvergen secara mutlak dan seragam pada himpunan tersebut X.

Bukti.

Untuk setiap ε > 0 detik ada nomor seperti itu N, itulah alasannya

Untuk sisa rn seri perkiraannya adil

Oleh karena itu, deret tersebut konvergen secara seragam.

Komentar. Prosedur pemilihan deret bilangan yang memenuhi syarat Teorema 40.1 biasa disebut mayoritasisasi , dan seri ini sendiri jurusan untuk rentang fungsional tertentu.

Contoh. Untuk jurusan seri fungsional untuk nilai berapa pun X adalah deret konvergen yang bertanda positif. Oleh karena itu, deret aslinya konvergen seragam menjadi (-∞, +∞).

Sifat-sifat deret konvergen seragam

Teorema 40.2. Jika fungsi kamu n (x) kontinu di dan deret tersebut konvergen seragam ke X, maka jumlahnya s (x) juga kontinu pada suatu titik x 0 .

Bukti.

Mari kita pilih ε > 0. Oleh karena itu, ada bilangan tersebut n 0 itu

- jumlah dari sejumlah fungsi kontinu yang terbatas, jadikontinu pada suatu titik x 0 . Oleh karena itu, terdapat δ > 0 sehingga Kemudian kita mendapatkan:

Artinya, fungsi s(x) kontinu di x = x 0.

Teorema 40.3. Biarkan fungsinya u n (x) kontinu pada interval [ a, b ] dan deret tersebut konvergen secara seragam pada segmen ini. Kemudian deret tersebut juga konvergen seragam ke [ a , b ] dan (40.2)

(yaitu, berdasarkan ketentuan teorema, deret tersebut dapat diintegrasikan suku demi suku).

Bukti.

Menurut Teorema 40.2 fungsinya s(x) = kontinu di [a, b ] dan, oleh karena itu, dapat diintegralkan di atasnya, yaitu integral di sisi kiri persamaan (40.2) ada. Mari kita tunjukkan bahwa deret tersebut konvergen seragam terhadap fungsinya

Mari kita tunjukkan

Maka untuk setiap ε ada nomor seperti itu N , yang untuk n > N

Artinya deret tersebut konvergen seragam, dan jumlahnya sama dengan σ ( x) = .

Teorema tersebut telah terbukti.

Teorema 40.4. Biarkan fungsinya u n (x) terdiferensiasi secara kontinyu pada interval [ a, b ] dan serangkaian turunannya:

(40.3)

menyatu secara seragam di [ a, b ]. Kemudian, jika suatu deret konvergen paling sedikit di satu titik, maka deret tersebut konvergen seragam di seluruh [ a , b ], jumlahnya s (x )= adalah fungsi terdiferensiasi kontinyu dan

(rangkaian tersebut dapat dibedakan suku demi suku).

Bukti.

Mari kita definisikan fungsinya σ( X ) Bagaimana. Berdasarkan Teorema 40.3, deret (40.3) dapat diintegrasikan suku demi suku:

Deret di sisi kanan persamaan ini konvergen seragam menjadi [ a, b ] menurut Teorema 40.3. Namun menurut syarat teorema, deret bilangan konvergen, oleh karena itu deret tersebut juga konvergen beraturan. Maka Fungsi σ( T ) adalah jumlah deret fungsi kontinu yang konvergen seragam pada [ a, b ] dan karena itu kontinu. Maka fungsinya dapat terdiferensiasi secara kontinyu pada [ a, b ], dan itulah yang perlu dibuktikan.

Definisi 41.1. Seri kekuatan disebut deret fungsional dari bentuk tersebut

(41.1)

Komentar. Menggunakan pengganti x x 0 = t deret (41.1) dapat direduksi menjadi bentuk, oleh karena itu cukup membuktikan semua sifat deret pangkat untuk deret berbentuk

(41.2)

Teorema 41.1 (Teorema 1 Habel).Jika deret pangkat (41.2) konvergen di x = x 0, maka untuk sembarang x: | x |< | x 0 | deret (41.2) konvergen mutlak. Jika deret (41.2) divergen di x = x 0, maka itu menyimpang untuk apa pun x: | x | > | x 0 |.

Bukti.

Jika deret tersebut konvergen maka terdapat konstanta c > 0:

Akibatnya, dan deret untuk | x |<| x 0 | konvergen karena merupakan jumlah barisan geometri yang menurun tak terhingga. Artinya deret di | x |<| x 0 | benar-benar cocok.

Jika diketahui deret (41.2) divergen di x = x 0 , maka tidak dapat konvergen di | x | > | x 0 | , karena dari apa yang telah dibuktikan sebelumnya maka akan konvergen pada suatu titik x 0 .

Jadi, jika Anda menemukan angka terbesar x 0 > 0 sehingga (41.2) konvergen x = x 0, maka daerah konvergensi deret tersebut, sebagai berikut dari teorema Abel, adalah interval (- x 0, x 0 ), mungkin mencakup salah satu atau kedua batas.

Definisi 41.2. Bilangan R ≥ 0 disebut radius konvergensideret pangkat (41.2), jika deret ini konvergen dan divergen. Interval (- R, R) disebut interval konvergensi seri (41.2).

Contoh.

1. Untuk mempelajari konvergensi mutlak suatu deret, kita menerapkan uji d'Alembert: . Oleh karena itu, deret tersebut konvergen hanya jika X = 0, dan jari-jari konvergensinya adalah 0: R = 0.
2. Dengan menggunakan uji d'Alembert yang sama, kita dapat menunjukkan bahwa deret tersebut konvergen untuk sembarang x, itu
3. Untuk deret yang menggunakan kriteria d'Alembert diperoleh:

Oleh karena itu, untuk 1< X < 1 ряд сходится, при

X< -1 и x > 1 menyimpang. Pada X = 1 kita memperoleh deret harmonik yang diketahui divergen, dan kapan X = -1 deret konvergen secara kondisional menurut kriteria Leibniz. Jadi, jari-jari konvergensi deret yang ditinjau R = 1, dan interval konvergensinya adalah [-1, 1).

Rumus untuk menentukan jari-jari konvergensi suatu deret pangkat.

1. rumus d'Alembert.

Mari kita perhatikan suatu deret pangkat dan menerapkan kriteria d'Alembert padanya: agar deret tersebut konvergen, diperlukan hal tersebut.Jika ada, maka daerah konvergensi ditentukan oleh pertidaksamaan, yaitu

- (41.3)

• rumus d'Alembertuntuk menghitung radius konvergensi.

1. Rumus Cauchy-Hadamard.

Dengan menggunakan uji radikal Cauchy dan penalaran dengan cara yang sama, kita menemukan bahwa kita dapat mendefinisikan daerah konvergensi suatu deret pangkat sebagai himpunan solusi terhadap pertidaksamaan, dengan adanya limit tersebut, dan, oleh karena itu, mencari rumus lain. untuk radius konvergensi:

(41.4)

• Rumus Cauchy-Hadamard.

Sifat-sifat deret pangkat.

Teorema 41.2 (Teorema ke-2 Habel). Jika R radius konvergensi deret (41.2) dan deret ini konvergen di x = R , maka konvergen seragam pada interval (- R, R).

Bukti.

Deret positif konvergen menurut Teorema 41.1. Akibatnya, deret (41.2) konvergen secara seragam pada interval [-ρ, ρ] menurut Teorema 40.1. Dari pilihan ρ maka interval konvergensi seragam (- R, R ), itulah yang perlu dibuktikan.

Akibat wajar 1 . Pada setiap segmen yang seluruhnya berada dalam interval konvergensi, jumlah deret (41.2) merupakan fungsi kontinu.

Bukti.

Suku-suku deret (41.2) merupakan fungsi kontinu, dan deret tersebut konvergen secara seragam pada interval yang ditinjau. Maka kontinuitas penjumlahannya mengikuti Teorema 40.2.

Akibat wajar 2. Jika limit integrasi α, β terletak pada interval konvergensi deret pangkat, maka integral jumlah deret tersebut sama dengan jumlah integral suku-suku deret tersebut:

(41.5)

Bukti pernyataan ini mengikuti Teorema 40.3.

Teorema 41.3. Jika deret (41.2) mempunyai interval konvergensi (- R, R), lalu deretnya

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +…+ na n x n- 1 +…, (41.6)

diperoleh dengan diferensiasi suku demi suku deret (41.2) mempunyai interval konvergensi yang sama (- R, R). Di mana

φ΄(x) = s΄ (x) untuk | x |< R , (41.7)

yaitu, dalam interval konvergensi, turunan dari jumlah suatu deret pangkat sama dengan jumlah deret yang diperoleh dari diferensiasi suku demi sukunya.

Bukti.

Mari kita pilih ρ: 0< ρ < R и ζ: ρ < ζ < R . Maka deret tersebut konvergen, yaitu Jika| x | ≤ ρ, lalu

Dengan demikian, suku-suku deret (41.6) memiliki nilai absolut yang lebih kecil dibandingkan suku-suku deret bertanda positif, yang konvergen menurut kriteria D’Alembert:

yaitu, merupakan jurusan untuk deret (41.6) karena Oleh karena itu, deret (41.6) konvergen secara seragam pada [-ρ, ρ]. Oleh karena itu, menurut Teorema 40.4, persamaan (41.7) benar. Dari pilihan ρ maka deret (41.6) konvergen pada sembarang titik dalam interval (- R, R).

Mari kita buktikan bahwa di luar interval ini deret (41.6) divergen. Memang benar, jika itu berkumpul di x 1 > R , kemudian, mengintegrasikannya suku demi suku pada interval (0, x 2 ), R< x 2 < x 1 , kita akan mendapatkan deret (41.2) yang konvergen di suatu titik x 2 , yang bertentangan dengan kondisi teorema. Jadi, teorema tersebut terbukti sepenuhnya.

Komentar . Deret (41.6), pada gilirannya, dapat dibedakan suku demi suku dan operasi ini dapat dilakukan sebanyak yang diinginkan.

Kesimpulan: jika deret pangkat konvergen pada interval (- R, R ), maka jumlahnya adalah suatu fungsi yang memiliki turunan sembarang ordo di dalam interval konvergensi, yang masing-masing merupakan jumlah dari suatu deret yang diperoleh dari deret aslinya dengan menggunakan diferensiasi suku demi suku sebanyak beberapa kali; Selain itu, interval konvergensi untuk serangkaian turunan orde apa pun adalah (- R, R).

Departemen Informatika dan Matematika Tinggi KSPU

Topik 2. Seri fungsional. Seri kekuatan

2.1. Seri fungsional

Sejauh ini kita telah membahas deret yang anggotanya berupa bilangan. Sekarang mari kita beralih ke pembahasan deret yang anggota-anggotanya adalah fungsi.

Rentang fungsional disebut baris

yang anggotanya merupakan fungsi dari argumen yang sama yang didefinisikan pada himpunan E yang sama.

Misalnya,

1.
;

2.
;

Jika kita memberikan argumennya X beberapa nilai numerik
,
, maka kita mendapatkan seri nomornya

yang dapat konvergen (konvergen secara mutlak) atau divergen.

Jika di
deret bilangan yang dihasilkan konvergen, lalu titik
ditelepontitik konvergensi rentang fungsional. Himpunan semua titik konvergensi disebutdaerah konvergensi rentang fungsional. Mari kita tunjukkan wilayah konvergensi X, jelas sekali,
.

Jika untuk deret bilangan bertanda positif yang diajukan pertanyaan: “Apakah deret tersebut konvergen atau divergen?”, untuk deret bolak-balik pertanyaannya adalah: “Apakah deret tersebut konvergen, bersyarat atau mutlak, atau divergen?”, maka untuk deret fungsional, pertanyaannya adalah: pertanyaan utamanya adalah: “Konvergen (konvergen secara mutlak) pada hal apa X?».

Rentang fungsional
menetapkan hukum yang sesuai dengan setiap nilai argumen
,
, diberi nomor yang sama dengan jumlah seri nomor tersebut
. Jadi, di lokasi syuting X fungsi ditentukan
, yang disebut jumlah deret fungsional.

Contoh 16.

Temukan area konvergensi deret fungsional

.

Larutan.

Membiarkan X adalah bilangan tetap, maka deret tersebut dapat dianggap sebagai deret bilangan yang bertanda positif bila
dan bergantian di
.

Mari kita buat rangkaian nilai absolut dari suku-suku rangkaian ini:

yaitu untuk nilai apa pun X batas ini kurang dari satu, yang berarti deret ini konvergen, dan mutlak (karena kita mempelajari deret nilai absolut suku-suku deret tersebut) pada seluruh sumbu numerik.

Jadi, daerah konvergensi mutlaknya adalah himpunan
.

Contoh 17.

Temukan area konvergensi deret fungsional
.

Larutan.

Membiarkan X– nomor tetap,
, maka deret tersebut dapat dianggap sebagai deret bilangan yang bertanda positif kapan
dan bergantian di
.

Mari kita perhatikan rangkaian nilai absolut suku-suku rangkaian ini:

dan terapkan uji D'Alembert padanya.

Berdasarkan uji DAlembert, suatu deret konvergen jika nilai limitnya kurang dari satu, yaitu. deret ini akan konvergen jika
.

Menyelesaikan pertidaksamaan ini, kita memperoleh:


.

Jadi, ketika , deret yang terdiri dari nilai absolut suku-suku deret tersebut konvergen, yang berarti deret aslinya konvergen secara mutlak, dan ketika
seri ini menyimpang.

Pada
deret tersebut dapat konvergen atau divergen, karena untuk nilai-nilai tersebut X nilai batasnya sama dengan kesatuan. Oleh karena itu, kami juga memeriksa konvergensi sejumlah titik
Dan
.

Mengganti di baris ini
, kita mendapatkan rangkaian angka
, yang diketahui merupakan deret divergen harmonis yang artinya titik
– titik divergensi suatu deret tertentu.

Pada
kita mendapatkan rangkaian bilangan bergantian

yang diketahui konvergen secara kondisional (lihat contoh 15), yang artinya titik
– titik konvergensi bersyarat dari deret tersebut.

Jadi, daerah konvergensi deret tersebut adalah , dan deret tersebut konvergen mutlak di .

Rentang fungsional

diteleponmenjadi mayoritas di suatu daerah variasi x, jika terdapat deret konvergen yang bertanda positif

,

bahwa untuk semua x dari wilayah ini kondisinya terpenuhi
pada
. Baris
diteleponjurusan.

Dengan kata lain, suatu deret didominasi jika masing-masing sukunya tidak lebih besar nilai absolutnya daripada suku-suku yang bersesuaian dari beberapa deret positif yang konvergen.

Misalnya saja sebuah serial

dapat diambil alih oleh siapa pun X, karena untuk semua orang X hubungan itu berlaku

pada
,

dan satu baris , seperti diketahui, bersifat konvergen.

DalilWeierstrass

Suatu deret yang mayoritas pada suatu wilayah tertentu konvergen secara mutlak pada wilayah tersebut.

Mari kita perhatikan, misalnya, deret fungsional
. Seri ini menjadi jurusan ketika
, sejak kapan
anggota deret tersebut tidak melebihi anggota deret positif yang bersesuaian . Akibatnya, menurut teorema Weierstrass, deret fungsional yang dianggap konvergen secara mutlak
.

2.2. Seri kekuatan. teorema Habel. Daerah konvergensi deret pangkat

Di antara berbagai deret fungsional, yang paling penting dari sudut pandang penerapan praktis adalah deret pangkat dan deret trigonometri. Mari kita lihat seri ini lebih detail.

Seri kekuatan sedikit demi sedikit
disebut deret fungsional dari bentuk tersebut

Di mana – beberapa nomor tetap,
– angka yang disebut koefisien seri.

Pada
kita mendapatkan rangkaian kekuatan dalam kekuatan X, yang memiliki bentuk

.

Untuk mempermudah, kita akan mempertimbangkan deret pangkat dalam pangkat X, karena dari rangkaian seperti itu mudah untuk memperoleh rangkaian pangkat
, sebagai gantinya X ekspresi
.

Kesederhanaan dan pentingnya kelas deret pangkat terutama disebabkan oleh fakta bahwa jumlah parsial dari suatu deret pangkat

adalah polinomial - fungsi yang propertinya dipelajari dengan baik dan nilainya mudah dihitung hanya dengan menggunakan operasi aritmatika.

Karena deret pangkat adalah kasus khusus dari deret fungsional, maka daerah konvergensinya juga perlu dicari. Berbeda dengan daerah konvergensi suatu deret fungsi sembarang yang dapat berupa himpunan dalam bentuk apa pun, daerah konvergensi suatu deret pangkat mempunyai bentuk yang pasti sepenuhnya. Teorema berikut menjelaskan hal ini.

DalilHabel.

Jika rangkaian pangkat
menyatu pada nilai tertentu
, maka ia konvergen secara mutlak untuk semua nilai x yang memenuhi kondisi tersebut
. Jika suatu deret pangkat menyimpang pada nilai tertentu
, kemudian menyimpang untuk nilai yang memenuhi kondisi tersebut
.

Dari teorema Abel berikut ini Semua titik konvergensi deret pangkat dalam pangkat X terletak dari titik asal koordinat tidak lebih jauh dari titik divergensi mana pun. Jelasnya, titik konvergensi mengisi celah tertentu yang berpusat di titik asal. teorema daerah konvergensi suatu deret pangkat adalah valid.

Dalil.

Untuk seri daya apa pun
ada nomorR (R>0)sedemikian rupa sehingga untuk semua x yang terletak di dalam interval
, deret tersebut konvergen secara mutlak dan untuk semua x yang terletak di luar interval
, rangkaiannya menyimpang.

NomorRditeleponradius konvergensi deret pangkat, dan interval
– interval konvergensi deret pangkat dalam pangkat x.

Perhatikan bahwa teorema tersebut tidak menjelaskan apa pun tentang konvergensi deret di ujung interval konvergensi, yaitu. di poin
. Pada titik-titik ini, deret pangkat yang berbeda berperilaku berbeda: deret tersebut dapat konvergen (secara absolut atau bersyarat), atau dapat menyimpang. Oleh karena itu, konvergensi deret pada titik-titik ini harus diperiksa secara langsung berdasarkan definisi.

Dalam kasus khusus, jari-jari konvergensi suatu deret bisa sama dengan nol atau tak terhingga. Jika
, lalu deret pangkat dalam pangkat X berkumpul pada satu titik saja
; jika
, maka deret pangkat konvergen pada seluruh sumbu bilangan.

Mari kita sekali lagi memperhatikan fakta bahwa rangkaian pangkat
sedikit demi sedikit
dapat direduksi menjadi deret pangkat
menggunakan penggantian
. Jika baris
menyatu di
, yaitu. Untuk
, lalu setelah substitusi terbalik kita dapatkan

 atau
.

Jadi, interval konvergensi deret pangkat
seperti
. Titik ditelepon pusat konvergensi. Untuk kejelasan, biasanya interval konvergensi digambarkan pada sumbu numerik (Gambar 1)

Jadi, daerah konvergensi terdiri dari interval konvergensi yang titik-titiknya dapat ditambahkan
, jika deret tersebut konvergen di titik-titik tersebut. Interval konvergensi dapat dicari dengan menerapkan langsung uji DAlembert atau uji radikal Cauchy pada suatu deret yang terdiri dari nilai absolut anggota deret tertentu.

Contoh 18.

Temukan luas konvergensi deret tersebut
.

Larutan.

Seri ini merupakan seri kekuatan dalam kekuatan X, yaitu.
. Mari kita perhatikan suatu deret yang terdiri dari nilai absolut anggota deret tersebut dan menggunakan tanda DAlembert.

Deret tersebut akan konvergen jika nilai limitnya kurang dari 1, yaitu.

, Di mana
.

Jadi, interval konvergensi deret ini
, radius konvergensi
.

Kami menyelidiki konvergensi deret di ujung interval, di titik-titik
. Mengganti nilai ke dalam seri ini
, kami mendapatkan serinya

.

Oleh karena itu, deret yang dihasilkan merupakan deret divergen harmonik pada intinya
deretnya divergen yang artinya suatu titik
tidak termasuk dalam wilayah konvergensi.

Pada
kami mendapatkan seri bergantian

,

yang konvergen bersyarat (contoh 15), itulah intinya
– titik konvergensi (bersyarat).

Jadi, daerah konvergensi deret tersebut
, dan pada intinya
Deret tersebut konvergen secara kondisional, dan pada titik lain konvergen secara mutlak.

Alasan yang digunakan untuk menyelesaikan contoh dapat bersifat umum.

Pertimbangkan deret pangkat

Mari kita menyusun deret nilai absolut anggota deret tersebut dan menerapkan tanda D'Alembert padanya.

Jika ada limit (berhingga atau tak terhingga), maka menurut syarat konvergensi kriteria D'Alembert, deret tersebut akan konvergen jika

,

,

.

Oleh karena itu, dari definisi interval dan jari-jari konvergensi, kita peroleh

Dengan menggunakan uji radikal Cauchy dan alasan serupa, kita dapat memperoleh rumus lain untuk mencari jari-jari konvergensi

Contoh 19

Larutan.

Seri ini merupakan seri kekuatan dalam kekuatan X. Untuk mencari interval konvergensi, kita menghitung jari-jari konvergensi menggunakan rumus di atas. Untuk deret tertentu, rumus koefisien numerik berbentuk

, Kemudian

Karena itu,

Karena R = , maka deret tersebut konvergen (dan mutlak) untuk semua nilai X, itu. wilayah konvergensi X (–; +).

Perhatikan bahwa daerah konvergensi dapat dicari tanpa menggunakan rumus, tetapi dengan menerapkan kriteria Alembert secara langsung:

Karena nilai limitnya tidak bergantung pada X dan kurang dari 1, maka deret tersebut konvergen untuk semua nilai X, itu. pada X(-;+).

Contoh 20

Temukan luas konvergensi deret tersebut

1!(X+5)+2!(X + 5) 2 +3!(X + 5) 3 +... + P!(X + 5) P +...

Larutan .

x+ 5), itu. pusat konvergensi X 0 = - 5. Koefisien numerik deret tersebut A P = n!.

Mari kita cari jari-jari konvergensi deret tersebut

.

Jadi, interval konvergensi terdiri dari satu titik - pusat interval konvergensi x = - 5.

Contoh 21

Temukan luas konvergensi deret tersebut
.

Larutan.

Deret ini merupakan deret pangkat dalam pangkat ( X–2), itu.

pusat konvergensi X 0 = 2. Perhatikan bahwa deret tersebut bertanda positif untuk setiap bilangan tetap X, sejak ekspresi ( X- 2) dipangkatkan 2 P. Mari kita terapkan uji Cauchy radikal pada rangkaian tersebut.

Deret tersebut akan konvergen jika nilai limitnya kurang dari 1, yaitu.

,
,
,

Artinya radius konvergensi
, maka integral konvergensi

,
.

Jadi, deret tersebut konvergen mutlak pada X
. Perhatikan bahwa integral konvergensi adalah simetris terhadap pusat konvergensi X HAI = 2.

Mari kita pelajari kekonvergenan deret pada ujung-ujung interval konvergensi.

Percaya
, kita memperoleh deret numerik dengan tanda positif

Mari kita gunakan kriteria konvergensi yang diperlukan:

oleh karena itu, deret bilangannya menyimpang, dan intinya
adalah titik divergensi. Perhatikan bahwa saat menghitung batasnya, kami menggunakan batas luar biasa kedua.

Percaya
, kita mendapatkan rangkaian angka yang sama (cek sendiri!), yang artinya titik
juga tidak termasuk dalam interval konvergensi.

Jadi, daerah konvergensi mutlak deret ini X
.

2.3. Sifat-sifat deret pangkat konvergen

Kita tahu bahwa jumlah terbatas dari fungsi kontinu adalah kontinu; jumlah fungsi yang terdiferensiasi dapat terdiferensiasi, dan turunan dari jumlah tersebut sama dengan jumlah turunannya; jumlah akhir dapat diintegrasikan suku demi suku.

Ternyata untuk “jumlah tak terhingga” dari fungsi—deret fungsi—propertinya tidak berlaku dalam kasus umum.

Misalnya, perhatikan deret fungsional

Jelas bahwa semua anggota deret tersebut merupakan fungsi kontinu. Mari kita cari daerah konvergensi deret ini dan jumlahnya. Untuk melakukan ini, kita mencari jumlah parsial dari deret tersebut

maka jumlah deretnya

Jadi jumlahnya S(X) suatu deret tertentu, sebagai limit suatu barisan jumlah parsial, ada dan berhingga X (-1;1), Artinya interval tersebut merupakan daerah konvergensi deret tersebut. Selain itu, jumlahnya adalah fungsi diskontinyu, karena

Jadi, contoh ini menunjukkan bahwa dalam kasus umum, sifat-sifat jumlah berhingga tidak memiliki analogi dengan jumlah tak terhingga - deret. Namun, untuk kasus khusus deret fungsional - deret pangkat - sifat-sifat penjumlahannya mirip dengan sifat-sifat jumlah berhingga.

– mungkin kompleksnya tidak akan terlalu rumit;) Dan judul artikel ini juga tidak jujur ​​​​- seri yang akan dibahas hari ini bukannya rumit, melainkan “rare earth”. Namun, bahkan siswa paruh waktu pun tidak kebal dari hal tersebut, dan oleh karena itu pelajaran tambahan ini harus ditanggapi dengan sangat serius. Lagi pula, setelah menyelesaikannya, Anda akan mampu menghadapi hampir semua "binatang buas"!

Mari kita mulai dengan genre klasik:

Contoh 1

Pertama, perhatikan bahwa ini BUKAN rangkaian pangkat (Saya mengingatkan Anda seperti apa). Dan kedua, di sini nilainya langsung menarik perhatian, yang jelas-jelas tidak bisa dimasukkan ke dalam daerah konvergensi deret tersebut. Dan ini sudah merupakan keberhasilan kecil dari penelitian ini!

Tapi tetap saja, bagaimana cara mencapai kesuksesan besar? Saya segera menyenangkan Anda - rangkaian seperti itu dapat diselesaikan dengan cara yang persis sama kekuatan– berdasarkan tanda d’Alembert atau tanda radikal Cauchy!

Larutan: nilainya tidak berada dalam rentang konvergensi deret tersebut. Ini adalah fakta penting dan harus diperhatikan!

Algoritma dasar berfungsi sebagai standar. Dengan menggunakan kriteria d'Alembert, kita mencari interval konvergensi deret tersebut:

Deret tersebut konvergen di . Mari kita pindahkan modul ke atas:

Mari kita segera periksa poin “buruknya”: nilainya tidak termasuk dalam rentang konvergensi deret tersebut.

Mari kita periksa konvergensi deret tersebut pada ujung “dalam” interval:
jika kemudian
jika kemudian

Kedua deret bilangan tersebut berbeda karena tanda konvergensi yang diperlukan.

Menjawab: daerah konvergensi:

Mari kita lakukan sedikit pemeriksaan analitis. Mari kita substitusikan beberapa nilai dari interval kanan ke dalam deret fungsional, misalnya:
– menyatu tanda d'Alembert.

Dalam hal mengganti nilai dari interval kiri, deret konvergen juga diperoleh:
jika kemudian .

Dan terakhir, jika , maka rangkaiannya – benar-benar berbeda.

Beberapa contoh sederhana untuk pemanasan:

Contoh 2

Temukan area konvergensi deret fungsional

Contoh 3

Temukan area konvergensi deret fungsional

Bersikaplah sangat baik dalam menangani hal-hal yang “baru” modul– itu akan terjadi 100.500 kali hari ini!

Solusi dan jawaban singkat di akhir pelajaran.

Algoritme yang digunakan tampaknya bersifat universal dan bebas masalah, namun kenyataannya tidak demikian - bagi banyak rangkaian fungsional, algoritma tersebut sering kali “tergelincir” dan bahkan mengarah pada kesimpulan yang salah. (Saya juga akan mempertimbangkan contoh-contoh seperti itu).

Kekasaran sudah dimulai pada tingkat interpretasi hasil: pertimbangkan, misalnya, rangkaian. Di sini, dalam batas yang kita dapatkan (periksa sendiri), dan secara teori Anda perlu memberikan jawaban bahwa deret tersebut konvergen pada satu titik. Namun, intinya “dimainkan”, artinya “sabar” kita tersebar kemana-mana!

Dan untuk sebuah seri, solusi Cauchy yang “jelas” tidak memberikan apa pun sama sekali:
– untuk nilai “x” APAPUN.

Dan timbul pertanyaan, apa yang harus dilakukan? Kami menggunakan metode yang akan menjadi bagian utama pelajaran! Dapat dirumuskan sebagai berikut:

Analisis langsung deret bilangan untuk berbagai nilai

Faktanya, kita sudah mulai melakukan hal ini pada Contoh 1. Pertama, kita memeriksa “X” tertentu dan deret bilangan yang sesuai. Itu meminta untuk mengambil nilai:
– deret bilangan yang dihasilkan divergen.

Dan ini langsung memunculkan pemikiran: bagaimana jika hal yang sama terjadi di tempat lain?
Mari kita periksa tanda penting dari kekonvergenan suatu deret Untuk sewenang-wenang arti:

Intinya diperhitungkan di atas, untuk semua orang “X” Kami akan mengaturnya sebagai standar batas indah kedua:

Kesimpulan: deret tersebut divergen sepanjang seluruh garis bilangan

Dan solusi ini adalah pilihan yang paling bisa diterapkan!

Dalam praktiknya, deret fungsional sering kali harus dibandingkan deret harmonik umum :

Contoh 4

Larutan: pertama-tama, mari kita berurusan dengan domain definisi: dalam hal ini, ekspresi radikal harus benar-benar positif, dan, sebagai tambahan, semua suku dalam deret tersebut harus ada, mulai dari suku ke-1. Oleh karena itu:
. Dengan nilai-nilai ini, diperoleh deret konvergen bersyarat:
dll.

Tanda “x” lainnya tidak cocok, jadi, misalnya, ketika kita mendapatkan kasus ilegal dimana dua suku pertama dari deret tersebut tidak ada.

Semuanya baik-baik saja, semuanya jelas, tetapi masih ada satu pertanyaan penting lagi - bagaimana cara memformalkan keputusan dengan benar? Saya mengusulkan skema yang dalam bahasa sehari-hari dapat disebut "menerjemahkan panah" ke deret angka:

Mari kita pertimbangkan sewenang-wenang arti dan mempelajari konvergensi deret bilangan. Rutin tanda Leibniz:

1) Deret ini bergantian.

2) – ketentuan penurunan modulus deret. Setiap anggota deret berikutnya memiliki modulo yang lebih kecil dari yang sebelumnya: , yang berarti penurunannya bersifat monoton.

Kesimpulan: deret tersebut konvergen menurut kriteria Leibniz. Seperti yang telah disebutkan, konvergensi di sini bersyarat - karena deretnya – menyimpang.

Begitu saja - rapi dan benar! Karena dibalik “alpha” kami dengan cerdik menyembunyikan semua rangkaian angka yang diperbolehkan.

Menjawab: deret fungsional ada dan konvergen secara kondisional di .

Contoh serupa untuk solusi independen:

Contoh 5

Selidiki konvergensi deret fungsional

Contoh perkiraan tugas akhir di akhir pembelajaran.

Sekian untuk “hipotesis kerja” Anda! – deret fungsional konvergen pada interval tersebut!

2) Dengan interval simetris semuanya transparan, pertimbangkan sewenang-wenang nilai dan kita mendapatkan: – deret bilangan yang benar-benar konvergen.

3) Dan terakhir, “tengah”. Di sini juga, akan lebih mudah untuk menyoroti dua celah.

Kami sedang mempertimbangkan sewenang-wenang nilai dari interval dan kita mendapatkan deret angka:

! Sekali lagi - jika itu sulit , gantikan nomor tertentu, misalnya. Namun... Anda menginginkan kesulitan =)

Selesai untuk semua nilai "en" , Cara:
- jadi, menurut perbandingan deret tersebut menyatu dengan perkembangan yang semakin menurun.

Untuk semua nilai “x” dari interval yang kita peroleh – deret bilangan yang benar-benar konvergen.

Semua “X” telah dieksplorasi, tidak ada lagi “X”!

Menjawab: rentang konvergensi deret tersebut:

Saya harus mengatakan, hasil yang tidak terduga! Dan perlu juga ditambahkan bahwa penggunaan tanda d'Alembert atau Cauchy di sini pasti menyesatkan!

Penilaian langsung adalah “aerobatik” analisis matematis, tetapi hal ini tentu saja memerlukan pengalaman, dan dalam beberapa kasus bahkan intuisi.

Atau mungkin seseorang akan menemukan cara yang lebih mudah? Menulis! Omong-omong, ada preseden - beberapa kali pembaca mengusulkan solusi yang lebih rasional, dan saya dengan senang hati menerbitkannya.

Selamat mendarat :)

Contoh 11

Temukan area konvergensi deret fungsional

Solusi versi saya sangat mirip.

Hardcore tambahan dapat ditemukan di Bagian VI (Baris) Koleksi Kuznetsov (Soal 11-13). Ada solusi siap pakai di Internet, tapi di sini saya membutuhkan Anda memperingatkan– banyak di antaranya tidak lengkap, salah, atau bahkan salah total. Dan omong-omong, inilah salah satu alasan mengapa artikel ini lahir.

Mari kita rangkum ketiga pembelajaran tersebut dan sistematiskan alat kita. Jadi:

Untuk mencari interval konvergensi suatu deret fungsi, Anda dapat menggunakan:

1) Tanda D'Alembert atau tanda Cauchy. Dan jika barisnya tidak tenang– kami menunjukkan peningkatan kehati-hatian saat menganalisis hasil yang diperoleh dengan substitusi langsung berbagai nilai.

2) Uji Weierstrass untuk konvergensi seragam. Jangan lupa!

3) Perbandingan dengan deret bilangan standar- aturan dalam kasus umum.

Kemudian periksa ujung interval yang ditemukan (jika diperlukan) dan kita memperoleh daerah konvergensi deret tersebut.

Sekarang Anda memiliki persenjataan yang cukup serius yang memungkinkan Anda mengatasi hampir semua tugas tematik.

Aku harap kamu berhasil!

Solusi dan jawaban:

Contoh 2: Larutan: nilainya tidak berada dalam rentang konvergensi deret tersebut.
Kami menggunakan tanda d'Alembert:


Deret tersebut konvergen di:

Jadi, interval konvergensi deret fungsional: .
Mari kita selidiki konvergensi deret tersebut pada titik-titik akhir:
jika kemudian ;
jika kemudian .
Kedua deret bilangan tersebut berbeda karena kriteria konvergensi yang diperlukan tidak terpenuhi.

Menjawab : daerah konvergensi: