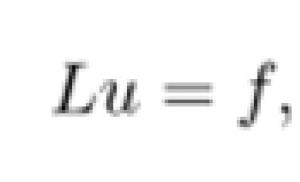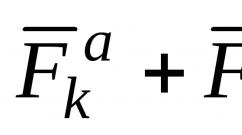Serii funcționale. Serii funcționale, regiunea de convergență, convergența uniformă, semnul Weierstrass, proprietățile serii funcționale uniform convergente, Convergența uniformă a unei serii funcționale și proprietățile acesteia

Aria de convergență O serie funcțională este o serie ai cărei membri sunt funcții / definite pe o anumită mulțime E a axei numerelor. De exemplu, termenii unei serii sunt definiți pe un interval, iar termenii unei serii sunt definiți pe un interval.Se spune că o serie funcțională (1) converge în punctul Ho € E dacă converge SERIE FUNCȚIONALĂ Regiunea de convergență Uniformă testul Weierstrass de convergență Proprietăți ale seriei funcționale uniform convergente seria numerică Dacă seria (1) converge în fiecare punct x al mulțimii D C E și diverge în fiecare punct care nu aparține mulțimii D, atunci se spune că seria converge către mulțimea D , iar D se numește regiunea de convergență a seriei. Se spune că o serie (1) este absolut convergentă pe o mulțime D dacă seria converge către această mulțime. În cazul convergenței unei serii (1) pe o mulțime D, suma sa S va fi o funcție definită pe D. Regiunea de convergență a unor serii funcționale poate fi găsită folosind criterii suficiente cunoscute stabilite pentru seriile cu termeni pozitivi, de exemplu, testul Dapambert, testul Cauchy. Exemplul 1. Aflați regiunea de convergență a seriei M Deoarece seria numerică converge pentru p > 1 și diverge pentru p ^ 1, atunci, presupunând p - Igx, obținem această serie. care va converge la Igx > T i.e. dacă x > 10 și diverge când Igx ^ 1, adică. la 0< х ^ 10. Таким образом, областью сходимости ряда является луч Пример 2. Найти область сходимости ряда 4 Рассмотрим ряд Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем пе При ех < 1. т.е. при, этот ряд будет сходиться. Следовательно, заданный ряд сходится абсолютно на интервале При х > Rândul 0 diverge, deoarece A =. Divergența seriei la x = 0 este evidentă. Exemplul 3. Aflați regiunea de convergență a seriei.Termenii seriei date sunt definiți și continui pe mulțime. Folosind criteriul Kosh și, găsim pentru orice. În consecință, seria diverge pentru toate valorile lui x. Să notăm cu Sn(x) a n-a sumă parțială a seriei funcționale (1). Dacă această serie converge către mulțimea D și suma ei este egală cu 5(g), atunci ea poate fi reprezentată sub forma în care este suma seriei convergentă către mulțimea D care se numește al n-lea rest al seriei funcționale ( 1). Pentru toate valorile lui x € D relația și, prin urmare, este valabilă. adică restul Rn(x) al unei serii convergente tinde spre zero ca n oo, oricare ar fi x 6 D. Convergenţă uniformă Dintre toate seriile funcţionale convergente, aşa-numitele serii uniform convergente joacă un rol important. Să fie dată o serie de funcții convergentă pe o mulțime D a cărei sumă este egală cu S(x). Să luăm a n-a sa sumă parțială Definiție. Serii funcționale SERIE FUNCȚIONALE Domeniu de convergență Convergență uniformă Testul Weierstrass Proprietățile serii funcționale uniform convergente se spune că sunt uniform convergente pe mulțimea PS1) dacă pentru orice număr e > O există un număr Γ > O astfel încât inegalitatea să fie valabilă pentru toate numerele n > N și pentru tot x din mulțimea fI. Cometariu. Aici numărul N este același pentru toate x € Yu, adică. nu depinde de z, ci depinde de alegerea numărului e, deci scriem N = N(e). Convergența uniformă a seriei funcționale £ /n(®) la funcția S(x) pe mulțimea ft se notează adesea astfel: Definiția convergenței uniforme a seriei /n(x) pe mulțimea ft poate fi scrisă mai pe scurt folosind simboluri logice: Să explicăm geometric sensul intervalului funcțional de convergență uniformă. Să luăm segmentul [a, 6] ca mulțime ft și să construim grafice ale funcțiilor. Inegalitatea |, care este valabilă pentru numerele n > N și pentru toate a; G [a, b], se poate scrie sub forma următoare.Inegalitățile obținute arată că graficele tuturor funcțiilor y = 5n(x) cu numere n > N vor fi cuprinse în întregime în banda £ limitată de curbele y = S(x) - e și y = 5(g) + e (Fig. 1). Exemplul 1 converge uniform asupra intervalului Această serie este alternativă în semn, satisface condițiile criteriului Leibniz pentru orice x € [-1,1] și, prin urmare, converge către intervalul (-1,1).Fie S(x ) fie suma sa, iar Sn (x) este suma sa parțială a n-a. Restul seriei în valoare absolută nu depășește valoarea absolută a primului său termen: și întrucât Să luăm orice e. Atunci inegalitatea | va fi satisfăcută dacă. De aici găsim că n > \. Dacă luăm un număr (aici [a] reprezintă cel mai mare număr întreg care nu depășește a), atunci inegalitatea | e va fi valabil pentru toate numerele n > N și pentru toate x € [-1,1). Aceasta înseamnă că această serie converge uniform pe intervalul [-1,1). I. Nu orice serie funcțională convergentă pe o mulțime D este uniform convergentă pe Exemplul 2. Să arătăm că seria converge pe un interval, dar nu uniform. 4 Să calculăm a n-a sumă parțială £„(*) a seriei. Avem Unde converge această serie spre segment și suma sa dacă Valoarea absolută a diferenței S(x) - 5„(x) (restul seriei) este egală. Să luăm un număr e astfel încât. Să rezolvăm inegalitatea față de n. Avem, de unde (deoarece și la împărțirea la Inx, semnul inegalității se schimbă în opus). Inegalitatea va fi satisfăcută când. Prin urmare, există un astfel de număr N(e) independent de x încât inegalitatea este satisfăcută pentru fiecare) pentru tot x din segment deodată. , nu exista. Dacă înlocuim segmentul 0 cu un segment mai mic, unde, atunci pe acesta din urmă această serie va converge uniform către funcția S0. De fapt, pentru, și deci pentru pentru toți x deodată §3. Testul lui Weierstrass Un test suficient pentru convergența uniformă a unei serii funcționale este dat de teorema lui Weierstrass. Teorema 1 (testul Weierstrass). Fie pentru toți x din mulțimea Q termenii seriei funcționale în valoare absolută să nu depășească membrii corespunzători ai seriei numerice convergente P = 1 cu termeni pozitivi, adică pentru toți x € Q. Atunci seria funcțională (1 ) pe mulţimea P converge absolut şi uniform . Și Tek deoarece, conform condițiilor teoremei, termenii seriei (1) îndeplinesc condiția (3) pe întreaga mulțime Q, atunci prin comparație seria 2 \fn(x)\ converge pentru orice x € I, și , în consecință, seria (1) converge către P în mod absolut. Să demonstrăm convergența uniformă a seriei (1). Fie Sn(x) și an sumele parțiale ale seriei (1) și respectiv (2). Avem Luați orice număr (arbitrar mic) e > 0. Apoi din convergența seriei de numere (2) rezultă existența unui număr N = N(e) astfel încât, deci, -e pentru toate numerele n > N (e) și pentru toate xbP , i.e. seria (1) converge uniform asupra multimii P. Observatie. Seria de numere (2) este adesea numită majorizantă, sau majorantă, pentru seria funcțională (1). Exemplul 1. Examinați seria pentru convergență uniformă.Inegalitatea este valabilă pentru toate. și pentru toată lumea. Seria de numere converge. În virtutea criteriului Weierstrass, seria funcțională luată în considerare converge absolut și uniform pe întreaga axă. Exemplul 2. Examinați seria pentru convergență uniformă.Termenii seriei sunt definiți și continui pe intervalul [-2,2|. Deoarece pe intervalul [-2,2) pentru orice număr natural n, atunci Astfel, inegalitatea este valabilă pentru. Deoarece seria de numere converge, atunci, conform criteriului lui Weierstrass, seria funcțională originală converge absolut și uniform pe segment. Cometariu. Seria funcțională (1) poate converge uniform asupra mulțimii Piv în cazul în care nu există o serie majorantă numerică (2), adică criteriul Weierstrass este doar un criteriu suficient pentru convergența uniformă, dar nu este necesar. Exemplu. După cum sa arătat mai sus (exemplu), seria converge uniform pe segmentul 1-1,1]. Cu toate acestea, pentru el nu există o serie de numere majorante convergente (2). De fapt, pentru tot n natural și pentru toți x € [-1,1) inegalitatea este satisfăcută și egalitatea este atinsă atunci când. Prin urmare, membrii seriei majorante dorite (2) trebuie să îndeplinească cu siguranță condiția, dar seria numerică SERIE FUNCȚIONALĂ Aria de convergență Convergență uniformă Testul Weierstrass Proprietățile seriei funcționale uniform convergente diverge. Aceasta înseamnă că și seria £op va diverge. Proprietățile serii funcționale uniform convergente Seriile funcționale uniform convergente au o serie de proprietăți importante. Teorema 2. Dacă toți termenii unei serii care converg uniform pe intervalul [a, b] sunt înmulțiți cu aceeași funcție d(x) mărginită la [a, 6], atunci seria funcțională rezultată va converge uniform pe. Fie pe intervalul [a, b\ seria £ fn(x) să convergă uniform către funcția 5(x), iar funcția d(x) să fie mărginită, adică există o constantă C > 0 astfel încât După definiție de convergență uniformă a seriei pentru orice număr e > 0 există un număr N astfel încât pentru toți n > N și pentru toți x € [a, b] inegalitatea va fi satisfăcută unde 5n(ar) este suma parțială a seria luată în considerare. Prin urmare, îl vom avea pentru toată lumea. seria converge uniform pe [a, b| la funcţia Teorema 3. Fie continuu toţi termenii fn(x) ai seriei funcţionale şi seria convergând uniform pe intervalul [a, b\. Atunci suma S(x) a seriei este continuă pe acest interval. M Să luăm două puncte arbitrare ig + Ax pe segmentul [o, b]. Deoarece această serie converge uniform pe intervalul [a, b], atunci pentru orice număr e > O există un număr N = N(e) astfel încât pentru tot i > N inegalitățile sunt satisfăcute unde 5„(g) sunt sume parțiale ale seriei fn (x). Aceste sume parțiale 5n(x) sunt continue pe intervalul [a, 6] ca sume ale unui număr finit de funcții fn(x) continue pe [a, 6]. Așadar, pentru un număr fix nu > N(e) și un număr dat e, există un număr 6 = 6(e) > 0 astfel încât pentru incrementul Ax care îndeplinește condiția |, inegalitatea se va menține: incrementul AS de suma S(x) poate fi reprezentată sub următoarea formă: unde. Ținând cont de inegalitățile (1) și (2), pentru incrementele Ax care îndeplinesc condiția |, obținem Aceasta înseamnă că suma șase) este continuă în punctul x. Deoarece x este un punct arbitrar al segmentului [a, 6], atunci 5(x) este continuu pe |a, 6|. Cometariu. O serie funcțională ai cărei termeni sunt continui pe intervalul [a, 6), dar care converge inegal pe (a, 6], poate avea o funcție discontinuă ca sumă. Exemplul 1. Să considerăm o serie funcțională pe intervalul |0,1 ). Să calculăm suma sa parțială a n-a. Prin urmare, este discontinuă pe segment, deși termenii seriei sunt continui pe acesta. În virtutea teoremei dovedite, această serie nu este uniform convergentă pe interval. Exemplul 2. Luați în considerare seria După cum se arată mai sus, această serie converge la, seria va converge uniform conform testului lui Weierstrass, deoarece 1 și seria de numere converg. În consecință, pentru orice x > 1 suma acestei serii este continuă. Cometariu. Funcția se numește funcție Riemann (această funcție joacă un rol important în teoria numerelor). Teorema 4 (cu privire la integrarea termen cu termen a unei serii funcționale). Fie toți termenii fn(x) ai seriei continui și seria converge uniform pe intervalul [a, b] către funcția S(x). Atunci egalitatea este valabilă: Datorită continuității funcțiilor f„(x) și a convergenței uniforme a acestei serii pe intervalul [a, 6], suma sa 5(x) este continuă și, deci, integrabilă pe . Să considerăm diferența Din convergența uniformă a seriei pe [o, b] rezultă că pentru orice e > 0 există un număr N(e) > 0 astfel încât pentru toate numerele n > N(e) și pentru toate x € [a, 6] inegalitatea va fi satisfăcută Dacă seria fn(0 nu este uniform convergentă, atunci, în general, nu poate fi integrată termen cu termen, adică Teorema 5 (la diferențierea termen cu termen a unei serii funcționale) Fie ca toți termenii seriei convergente 00 au derivate continue și seria compusă din aceste derivate, converge uniform pe intervalul [a, b] Atunci în orice moment egalitatea este adevărată, adică această serie poate fi diferențiată termen prin termen.M Să luăm oricare două puncte.Atunci, în virtutea teoremei 4, vom avea Funcția o-(x) este continuă ca suma unei serii uniform convergente de funcții continue.De aceea, diferențiind egalitatea obținem Exerciții Aflați ariile de convergență ale acestor serii funcționale: Folosind testul Weierstrass, demonstrați convergența uniformă a acestor serii funcționale pe intervalele indicate:

Gama funcțională se numește expresie scrisă formal

u1 (X) + u 2 (X) + u 3 (X) + ... + u n( X) + ... , (1)

Unde u1 (X), u 2 (X), u 3 (X), ..., u n( X), ... - succesiunea de funcţii din variabila independentă X.

Notarea prescurtată a unei serii funcționale cu sigma: .

Exemple de serii funcționale includ :

(2)

(3)

Dând variabila independentă X ceva valoare X0 iar substituind-o in seria functionala (1), obtinem seria numerica

u1 (X 0 ) + u 2 (X 0 ) + u 3 (X 0 ) + ... + u n( X 0 ) + ...

Dacă seria numerică rezultată converge, atunci seria funcțională (1) se spune că converge pentru X = X0 ; dacă diverge, ceea ce se spune este că seria (1) diverge la X = X0 .

Exemplul 1. Investigați convergența unei serii funcționale(2) la valori X= 1 și X = - 1 .
Soluţie. La X= 1 obținem o serie de numere

care converge după criteriul lui Leibniz. La X= - 1 obținem o serie de numere

,

care diverge ca produsul unei serii armonice divergente cu – 1. Deci, seria (2) converge la X= 1 și diverge la X = - 1 .

Dacă o astfel de verificare a convergenței seriei funcționale (1) este efectuată cu privire la toate valorile variabilei independente din domeniul de definire a membrilor săi, atunci punctele acestui domeniu vor fi împărțite în două seturi: pentru valori X, luată într-una dintre ele, seria (1) converge, iar în cealaltă diverge.

Setul de valori ale variabilei independente la care converge seria funcțională se numește ei zona de convergenta .

Exemplul 2. Găsiți aria de convergență a seriei funcționale

Soluţie. Termenii seriei sunt definiți pe întreaga linie numerică și formează o progresie geometrică cu un numitor q= păcat X. Prin urmare seria converge dacă

şi diverge dacă

(valori nu sunt posibile). Dar pentru valori și pentru alte valori X. Prin urmare, seria converge pentru toate valorile X, cu exceptia . Regiunea de convergență este întreaga dreaptă numerică, cu excepția acestor puncte.

Exemplul 3. Găsiți aria de convergență a seriei funcționale

Soluţie. Termenii seriei formează o progresie geometrică cu numitorul q=ln X. Prin urmare, seria converge dacă , sau , de unde . Aceasta este regiunea de convergență a acestei serii.

Exemplul 4. Investigați convergența unei serii funcționale

Soluţie. Să luăm o valoare arbitrară. Cu această valoare obținem o serie de numere

(*)

Să găsim limita termenului său comun

În consecință, seria (*) diverge pentru un ales arbitrar, adică. la orice valoare X. Regiunea sa de convergență este mulțimea goală.

Convergența uniformă a unei serii funcționale și proprietățile acesteia

Să trecem la concept convergenţa uniformă a seriei funcţionale . Lăsa s(X) este suma acestei serii și sn( X) - suma n primii membri ai acestei serii. Gama funcțională u1 (X) + u 2 (X) + u 3 (X) + ... + u n( X) + ... se numeste uniform convergent pe intervalul [ A, b] , dacă pentru orice număr arbitrar mic ε > 0 există un astfel de număr N că în fața tuturor n ≥ N inegalitatea va fi îndeplinită

|s(X) − s n( X)| < ε

pentru oricine X din segmentul [ A, b] .

Proprietatea de mai sus poate fi ilustrată geometric după cum urmează.

Luați în considerare graficul funcției y = s(X) . Să construim o bandă de lățime 2 în jurul acestei curbe ε n, adică vom construi curbe y = s(X) + ε nȘi y = s(X) − ε n(in poza de mai jos sunt verzi).

Apoi pentru orice ε n graficul unei funcții sn( X) va fi în întregime în banda luată în considerare. Aceeași bandă va conține grafice ale tuturor sumelor parțiale ulterioare.

Orice serie funcțională convergentă care nu are caracteristica descrisă mai sus este convergentă neuniform.

Să luăm în considerare o altă proprietate a serii funcționale uniform convergente:

suma unei serii de funcții continue care converg uniform într-un anumit interval [ A, b] , există o funcție continuă pe acest interval.

Exemplul 5. Determinați dacă suma unei serii funcționale este continuă

Soluţie. Să găsim suma n primii membri ai acestei serii:

Dacă X> 0, atunci

,

Dacă X < 0 , то

Dacă X= 0, atunci

Prin urmare .

Cercetările noastre au arătat că suma acestei serii este o funcție discontinuă. Graficul său este prezentat în figura de mai jos.

Testul Weierstrass pentru convergența uniformă a seriilor funcționale

Abordăm criteriul Weierstrass prin intermediul conceptului majorizarea seriei funcţionale . Gama funcțională

u1 (X) + u 2 (X) + u 3 (X) + ... + u n( X) + ...

Luhov Yu.P. Note de curs despre matematica superioară. Prelegerea nr. 42 5

Cursul 42

SUBIECT: Serii funcționale

Plan.

1. Serii funcționale. Regiunea de convergență.
2. Convergență uniformă. semn Weierstrass.
3. Proprietățile seriei uniform convergente: continuitatea sumei seriei, integrarea și diferențierea termen cu termen.
4. Serie de puteri. teorema lui Abel. Regiunea de convergență a seriei de puteri. Raza de convergență.
5. Proprietățile de bază ale seriei de puteri: convergența uniformă, continuitatea și diferențiabilitatea infinită a sumei. Integrarea și diferențierea termen cu termen a serii de puteri.

Serii funcționale. Regiunea de convergență

Definiția 40.1. Număr infinit de funcții

u 1 (x) + u 2 (x) +…+ u n (x) +…, (40.1)

unde u n (x) = f (x, n), se numește gamă funcțională.

Dacă specificați o anumită valoare numerică X , seria (40.1) se va transforma într-o serie de numere, iar în funcție de alegerea valorii X o astfel de serie poate converge sau diverge. Numai seriile convergente au valoare practică, deci este important să se determine acele valori X , la care seria funcțională devine o serie numerică convergentă.

Definiția 40.2. Sensuri multiple X , la substituirea lor in seria functionala (40.1) se obtine o serie numerica convergenta, se numestezona de convergentagamă funcțională.

Definiția 40.3. Funcția s(x), definite în regiunea de convergenţă a seriei, care pentru fiecare valoare X din regiunea de convergență este egală cu suma seriei numerice corespunzătoare obținute din (40.1) pentru o valoare dată x este numit suma seriei funcționale.

Exemplu. Să găsim regiunea de convergență și suma seriei funcționale

1 + x + x² +…+ x n +…

Când | X | ≥ 1, prin urmare, seria de numere corespunzătoare diverge. Dacă

| X | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:

În consecință, domeniul de convergență al seriei este intervalul (-1, 1), iar suma acestuia are forma indicată.

cometariu . La fel ca și pentru seria de numere, puteți introduce conceptul de sumă parțială a unei serii funcționale:

s n = 1 + x + x² +…+ x n

iar restul seriei: r n = s s n .

Convergența uniformă a unei serii funcționale

Să definim mai întâi conceptul de convergență uniformă a unei secvențe de numere.

Definiția 40.4. Secvență funcțională se numește fn(x). convergând uniform către funcţie f pe multimea X daca si

Nota 1. Vom nota convergența obișnuită a unei secvențe funcționale și convergența uniformă cu .

Nota 2 . Să remarcăm încă o dată diferența fundamentală dintre convergența uniformă și convergența obișnuită: în cazul convergenței obișnuite, pentru o valoare aleasă a lui ε, pentru fiecare există numărul tău N, pentru care la n>N inegalitatea este valabilă:

În acest caz, se poate dovedi că pentru un ε dat numărul general N, asigurând îndeplinirea acestei inegalităţi pentru oricare X , imposibil. În cazul convergenței uniforme, un astfel de număr N, comun tuturor x, există.

Să definim acum conceptul de convergență uniformă a unei serii funcționale. Deoarece fiecare serie corespunde unei secvențe a sumelor sale parțiale, convergența uniformă a seriei este determinată prin convergența uniformă a acestei secvențe:

Definiția 40.5. Seria funcțională se numeșteuniform convergente pe setul X, dacă pe X succesiunea sumelor sale parțiale converge uniform.

semn Weierstrass

Teorema 40.1. Dacă o serie de numere converge atât pentru toată lumea, cât și pentru toată lumea n = 1, 2,... inegalitatea este satisfăcută atunci seria converge absolut și uniform pe mulțime X.

Dovada.

Pentru orice ε > 0 s există un astfel de număr N, motiv pentru care

Pentru resturile r n serie estimarea este corectă

Prin urmare, seria converge uniform.

Cometariu. Procedura de selectare a unei serii de numere care îndeplinește condițiile teoremei 40.1 este de obicei numită majorare , și această serie în sine majorante pentru un interval funcțional dat.

Exemplu. Pentru o serie funcțională majorant pentru orice valoare X este o serie convergentă cu semn pozitiv. Prin urmare, seria originală converge uniform către (-∞, +∞).

Proprietățile serii uniform convergente

Teorema 40.2. Dacă funcțiile u n (x) sunt continue la și seria converge uniform către X, atunci suma sa s (x) este, de asemenea, continuă într-un punct x 0 .

Dovada.

Să alegem ε > 0. Atunci, deci, există un astfel de număr n 0 că

- suma unui număr finit de funcții continue, decicontinuu la un punct x 0 . Prin urmare, există un δ > 0 astfel încât Atunci obținem:

Adică, funcția s (x) este continuă la x = x 0.

Teorema 40.3. Fie funcțiile u n (x) continuu pe intervalul [ a, b ] iar seria converge uniform pe acest segment. Apoi seria converge uniform spre [ a , b ] și (40.2)

(adica in conditiile teoremei seria poate fi integrata termen cu termen).

Dovada.

Prin teorema 40.2 funcţia s(x) = continuu pe [a, b ] și, prin urmare, este integrabil pe ea, adică integrala din partea stângă a egalității (40.2) există. Să arătăm că seria converge uniform către funcție

Să notăm

Atunci pentru orice ε există un astfel de număr N, care pentru n > N

Aceasta înseamnă că seria converge uniform, iar suma sa este egală cu σ ( x) = .

Teorema a fost demonstrată.

Teorema 40.4. Fie funcțiile u n (x) sunt diferențiabile continuu pe intervalul [ a, b ] și o serie compusă din derivatele lor:

(40.3)

converge uniform spre [ a, b ]. Atunci, dacă o serie converge cel puțin într-un punct, atunci converge uniform în [ a , b ], suma sa s (x )= este o funcţie continuu diferenţiabilă şi

(seria poate fi diferenţiată termen cu termen).

Dovada.

Să definim funcția σ( X ) Cum. Prin teorema 40.3, seria (40.3) poate fi integrată termen cu termen:

Seria din partea dreaptă a acestei egalități converge uniform către [ a, b ] prin teorema 40.3. Dar, conform condițiilor teoremei, seria de numere converge, prin urmare, și seria converge uniform. Atunci funcția σ( t ) este suma unei serii uniform convergente de funcții continue pe [ a, b ] și, prin urmare, este ea însăși continuă. Atunci funcția este diferențiabilă continuu pe [ a, b ], iar asta trebuia demonstrat.

Definiția 41.1. Serie de puteri se numește o serie funcțională a formei

(41.1)

Cometariu. Folosind înlocuire x x 0 = t seria (41.1) poate fi redusă la forma, de aceea este suficient să se demonstreze toate proprietățile seriei de puteri pentru serii de formă

(41.2)

Teorema 41.1 (Teorema I a lui Abel).Dacă seria de puteri (41.2) converge la x = x 0, atunci pentru orice x: | x |< | x 0 | seria (41.2) converge absolut. Dacă seria (41.2) diverge la x = x 0, apoi diverge pentru oricare x: | x | > | x 0 |.

Dovada.

Dacă seria converge, atunci există o constantă c > 0:

În consecință, și seria pentru | x |<| x 0 | converge deoarece este suma unei progresii geometrice infinit descrescătoare. Aceasta înseamnă că seria de la | x |<| x 0 | se potriveste absolut.

Dacă se știe că seria (41.2) diverge la x = x 0 , atunci nu poate converge la | x | > | x 0 | , întrucât din cele dovedite anterior ar rezulta că converge la punct x 0 .

Astfel, dacă găsiți cel mai mare număr x 0 > 0 astfel încât (41.2) converge pentru x = x 0, atunci regiunea de convergență a acestei serii, după cum reiese din teorema lui Abel, va fi intervalul (- x 0, x 0 ), eventual incluzând una sau ambele granițe.

Definiția 41.2. Se numește numărul R ≥ 0 raza de convergentaserie de puteri (41.2), dacă această serie converge și diverge. Interval (- R, R) se numește interval de convergenta seria (41.2).

Exemple.

1. Pentru a studia convergența absolută a unei serii, aplicăm testul d’Alembert: . Prin urmare, seria converge numai atunci când X = 0, iar raza sa de convergență este 0: R = 0.
2. Folosind același test d'Alembert, putem arăta că seria converge pentru oricare x, adică
3. Pentru o serie care folosește criteriul lui d'Alembert obținem:

Prin urmare, pentru 1< X < 1 ряд сходится, при

X< -1 и x > 1 diverge. La X = 1 obținem o serie armonică, care, după cum se știe, diverge și când X = -1 serie converge conditionat dupa criteriul Leibniz. Astfel, raza de convergență a seriei luate în considerare R = 1, iar intervalul de convergență este [-1, 1).

Formule pentru determinarea razei de convergență a unei serii de puteri.

1. formula lui d'Alembert.

Să considerăm o serie de puteri și să-i aplicăm criteriul lui d'Alembert: pentru ca seria să converge, este necesar ca. Dacă există, atunci regiunea de convergență este determinată de inegalitate, adică

- (41.3)

• formula lui d'Alembertpentru a calcula raza de convergență.

1. Formula Cauchy-Hadamard.

Folosind testul radical Cauchy și raționând în mod similar, constatăm că putem defini regiunea de convergență a unei serii de puteri ca un set de soluții ale inegalității, sub rezerva existenței acestei limite și, în consecință, găsim o altă formulă. pentru raza de convergență:

(41.4)

• Formula Cauchy-Hadamard.

Proprietățile seriei de putere.

Teorema 41.2 (a 2-a teoremă a lui Abel). Daca R raza de convergență a seriei (41.2) și această serie converge la x = R , apoi converge uniform pe intervalul (- R, R).

Dovada.

O serie pozitivă converge prin teorema 41.1. În consecință, seria (41.2) converge uniform în intervalul [-ρ, ρ] prin Teorema 40.1. Din alegerea lui ρ rezultă că intervalul de convergență uniformă (- R, R ), ceea ce trebuia dovedit.

Corolarul 1 . Pe orice segment care se află în întregime în intervalul de convergență, suma seriei (41.2) este o funcție continuă.

Dovada.

Termenii seriei (41.2) sunt funcții continue, iar seria converge uniform asupra intervalului luat în considerare. Apoi continuitatea sumei sale rezultă din teorema 40.2.

Corolarul 2. Dacă limitele integrării α, β se află în intervalul de convergență al seriei de puteri, atunci integrala sumei seriei este egală cu suma integralelor termenilor seriei:

(41.5)

Dovada acestei afirmații rezultă din teorema 40.3.

Teorema 41.3. Dacă seria (41.2) are un interval de convergență (- R, R), apoi seria

φ (x) = a 1 + 2 a 2 x + 3 a 3 x ² +…+ na n x n- 1 +…, (41.6)

obţinut prin diferenţierea termen cu termen a seriei (41.2) are acelaşi interval de convergenţă (- R, R). în care

φ΄(x) = s΄ (x) pentru | x |< R , (41.7)

adică în intervalul de convergenţă, derivata sumei unei serii de puteri este egală cu suma seriei obţinută prin diferenţierea ei termen cu termen.

Dovada.

Să alegem ρ: 0< ρ < R и ζ: ρ < ζ < R . Atunci seria converge, deci, adică Dacă| x | ≤ ρ, atunci

Unde Astfel, termenii seriei (41.6) sunt mai mici în valoare absolută decât termenii seriei cu semn pozitiv, care converge după criteriul lui D’Alembert:

adică este majorant pentru seria (41.6) pentru Prin urmare, seria (41.6) converge uniform pe [-ρ, ρ]. Prin urmare, prin teorema 40.4, egalitatea (41.7) este adevărată. Din alegerea lui ρ rezultă că seria (41.6) converge în orice punct interior al intervalului (- R, R).

Să demonstrăm că în afara acestui interval seria (41.6) diverge. Într-adevăr, dacă ar converge la x 1 > R , apoi, integrându-l termen cu termen pe intervalul (0, x2), R< x 2 < x 1 , am obține că seria (41.2) converge în punctul x 2 , ceea ce contrazice condițiile teoremei. Deci, teorema este complet demonstrată.

cometariu . Seria (41.6), la rândul ei, poate fi diferențiată termen cu termen și această operație poate fi efectuată de câte ori se dorește.

Concluzie: dacă seria de puteri converge pe intervalul (- R, R ), atunci suma ei este o funcție care are derivate de orice ordin în interiorul intervalului de convergență, fiecare dintre acestea fiind suma unei serii obținute din cea originală folosind diferențierea termen cu termen de numărul corespunzător de ori; Mai mult, intervalul de convergență pentru o serie de derivate de orice ordin este (- R, R).

Departamentul de Informatică și Matematică Superioară KSPU

Tema 2. Serii funcționale. Serie de puteri

2.1. Serii funcționale

Până acum am luat în considerare seriale ai căror membri erau numere. Să trecem acum la studiul seriilor ai căror membri sunt funcții.

Gama funcțională numită rând

ai căror membri sunt funcții ale aceluiași argument definit pe aceeași mulțime E.

De exemplu,

1.
;

2.
;

Dacă dăm argumentul X o anumită valoare numerică
,
, apoi obținem seria de numere

care poate converge (converge absolut) sau diverge.

Eu gras
seria de numere rezultată converge, apoi punctul
numitpunct de convergență gamă funcțională. Se numește mulțimea tuturor punctelor de convergențăzona de convergenta gamă funcțională. Să notăm regiunea de convergență X, evident,
.

Dacă pentru seriile numerice cu semn pozitiv se pune întrebarea: „Converge sau diverge seria?”, pentru serii alternante se pune întrebarea: „Converge, condiționat sau absolut, sau diverge?”, atunci pentru o serie funcțională se pune întrebarea: întrebarea principală este: „Converge (converge absolut) la ce X?».

Gama funcțională
stabileşte o lege conform căreia fiecare valoare a argumentului
,
, i se atribuie un număr egal cu suma seriei de numere
. Astfel, pe platou X este specificată funcția
, Care e numit suma seriei funcționale.

Exemplul 16.

Găsiți aria de convergență a seriei funcționale

.

Soluţie.

Lăsa X este un număr fix, atunci această serie poate fi considerată ca o serie de numere cu semn pozitiv când
şi alternând la
.

Să facem o serie de valori absolute ale termenilor acestei serii:

adică pentru orice valoare X această limită este mai mică de unu, ceea ce înseamnă că această serie converge și absolut (deoarece am studiat o serie de valori absolute ale termenilor seriei) pe întreaga axă numerică.

Astfel, regiunea de convergență absolută este mulțimea
.

Exemplul 17.

Găsiți aria de convergență a seriei funcționale
.

Soluţie.

Lăsa X– număr fix,
, atunci această serie poate fi considerată ca o serie de numere cu semn pozitiv când
şi alternând la
.

Să luăm în considerare o serie de valori absolute ale termenilor acestei serii:

și aplică-i testul lui D'Alembert.

Conform testului lui DAlembert, o serie converge dacă valoarea limită este mai mică de unu, adică. această serie va converge dacă
.

Rezolvând această inegalitate, obținem:


.

Astfel, atunci când , seria compusă din valorile absolute ale termenilor acestei serii converge, ceea ce înseamnă că seria inițială converge absolut, iar când
această serie diverge.

La
seria poate converge sau diverge, deoarece pentru aceste valori X valoarea limită este egală cu unitatea. Prin urmare, examinăm suplimentar convergența unui număr de puncte
Și
.

Înlocuind în acest rând
, obținem o serie de numere
, despre care se știe că este o serie divergentă armonică, ceea ce înseamnă punctul
– punctul de divergență al unei serii date.

La
obținem o serie de numere alternativă

despre care se știe că converge condiționat (vezi exemplul 15), ceea ce înseamnă punctul
– punctul de convergență condiționată a seriei.

Astfel, regiunea de convergență a acestei serii este , iar seria converge absolut la .

Gama funcțională

numitmajorat într-o regiune de variație a lui x, dacă există o astfel de serie convergentă de semn pozitiv

,

că pentru toți x din această regiune condiția este îndeplinită
la
. Rând
numitmajorante.

Cu alte cuvinte, o serie este dominată dacă fiecare dintre termenii săi nu este mai mare în valoare absolută decât termenul corespunzător al unei serii pozitive convergente.

De exemplu, o serie

este majorizabil pentru orice X, pentru că pentru toată lumea X relatia tine

la
,

și un rând , după cum se știe, este convergent.

TeoremaWeierstrass

O serie care este majorată într-o anumită regiune converge absolut în acea regiune.

Să luăm în considerare, de exemplu, seria funcțională
. Această serie este majorată când
, de cand
membrii seriei nu depășesc membrii corespunzători ai seriei pozitive . În consecință, conform teoremei Weierstrass, seria funcțională considerată converge absolut pentru
.

2.2. Serie de puteri. teorema lui Abel. Regiunea de convergență a seriei de puteri

Dintre varietatea de serii funcționale, cele mai importante din punct de vedere al aplicării practice sunt seriile de putere și trigonometrice. Să ne uităm la aceste serii mai detaliat.

Serie de puteri treptat
se numește o serie funcțională a formei

Unde – un număr fix,
– numere numite coeficienți de serie.

La
obținem o serie de puteri în puteri X, care are forma

.

Pentru simplitate, vom lua în considerare seriile de putere în puteri X, întrucât dintr-o astfel de serie se obține ușor o serie în puteri
, înlocuind în schimb X expresie
.

Simplitatea și importanța clasei de serie de puteri se datorează în primul rând faptului că suma parțială a unei serii de puteri

este un polinom - o funcție ale cărei proprietăți sunt bine studiate și ale cărei valori sunt ușor de calculat folosind numai operații aritmetice.

Deoarece seriile de putere sunt un caz special al unei serii funcționale, este, de asemenea, necesar să se găsească regiunea de convergență pentru ele. Spre deosebire de domeniul de convergență al unei serii funcționale arbitrare, care poate fi o mulțime de orice formă, domeniul de convergență al unei serii de puteri are o formă complet definită. Următoarea teoremă vorbește despre asta.

TeoremaAbel.

Dacă seria de putere
converge la o anumită valoare
, apoi converge, absolut, pentru toate valorile lui x care satisfac condiția
. Dacă o serie de puteri diverge la o anumită valoare
, apoi diverge pentru valori care satisfac condiția
.

Din teorema lui Abel rezultă că Toate punctele de convergenţă ale serii de puteri în puteri X situat de la originea coordonatelor nu mai departe decât oricare dintre punctele de divergență. Evident, punctele de convergență umplu un anumit gol centrat la origine. este valabilă teorema asupra regiunii de convergenţă a unei serii de puteri.

Teorema.

Pentru orice serie de putere
există un numărR (R>0)astfel încât pentru toate x situate în interiorul intervalului
, seria converge absolut și pentru toate x situate în afara intervalului
, seria diverge.

NumărRnumitraza de convergenta seria de putere și intervalul
– interval de convergenta serie de puteri în puteri ale lui x.

Rețineți că teorema nu spune nimic despre convergența seriei la capetele intervalului de convergență, i.e. la puncte
. În aceste puncte, diferitele serii de putere se comportă diferit: seria poate converge (absolut sau condiționat) sau poate diverge. Prin urmare, convergența seriei în aceste puncte ar trebui verificată direct prin definiție.

În cazuri speciale, raza de convergență a unei serii poate fi egală cu zero sau infinit. Dacă
, apoi seria de puteri în puteri X converge doar într-un singur punct
; dacă
, apoi seria de puteri converge pe întreaga axă a numerelor.

Să acordăm încă o dată atenție faptului că seria de putere
treptat
poate fi redusă la o serie de puteri
folosind înlocuirea
. Dacă rândul
converge la
, adică Pentru
, apoi după înlocuirea inversă obținem

 sau
.

Astfel, intervalul de convergență al seriei de puteri
se pare ca
. Punct numit centru de convergenţă. Pentru claritate, este obișnuit să se descrie intervalul de convergență pe axa numerică (Figura 1)

Astfel, regiunea de convergență constă dintr-un interval de convergență la care se pot adăuga puncte
, dacă seria converge în aceste puncte. Intervalul de convergență poate fi găsit prin aplicarea directă a testului lui DAlembert sau a testului radical al lui Cauchy la o serie compusă din valorile absolute ale membrilor unei serii date.

Exemplul 18.

Găsiți aria de convergență a seriei
.

Soluţie.

Această serie este o serie de puteri în puteri X, adică
. Să considerăm o serie alcătuită din valorile absolute ale membrilor acestei serii și să folosim semnul lui DAlembert.

Seria va converge dacă valoarea limită este mai mică de 1, adică.

, Unde
.

Astfel, intervalul de convergență al acestei serii
, raza de convergență
.

Investigam convergenta seriei la capetele intervalului, la puncte
. Înlocuirea valorii în această serie
, primim seria

.

Seria rezultată este o serie divergentă armonică, prin urmare, la punct
seria diverge, ceea ce înseamnă un punct
nu este inclusă în regiunea de convergenţă.

La
obținem o serie alternativă

,

care este convergent condiționat (exemplul 15), de aici punctul
– punct de convergenţă (condiţional).

Astfel, regiunea de convergență a seriei
, iar la punct
Seria converge condiționat, iar în alte puncte converge absolut.

Raționamentului folosit pentru rezolvarea exemplului i se poate da un caracter general.

Luați în considerare seria de putere

Să compilam o serie de valori absolute ale membrilor seriei și să aplicăm criteriul lui D'Alembert.

Dacă există o limită (finită sau infinită), atunci conform condiției de convergență a criteriului lui D'Alembert, seria va converge dacă

,

,

.

Prin urmare, din definiția intervalului și a razei de convergență, avem

Folosind testul radical Cauchy și raționând în mod similar, putem obține o altă formulă pentru găsirea razei de convergență

Exemplul 19

Soluţie.

Seria este o serie de puteri în puteri X. Pentru a găsi intervalul de convergență, calculăm raza de convergență folosind formula de mai sus. Pentru o serie dată, formula coeficientului numeric are forma

, Apoi

Prin urmare,

Deoarece R = , atunci seria converge (și absolut) pentru toate valorile X, acestea. regiune de convergenţă X (–; +).

Rețineți că ar fi posibil să găsiți regiunea de convergență fără a folosi formule, dar prin aplicarea directă a criteriului lui Alembert:

Deoarece valoarea limitei nu depinde de Xși mai puțin de 1, atunci seria converge pentru toate valorile X, acestea. la X(-;+).

Exemplul 20

Găsiți aria de convergență a seriei

1!(X+5)+2!(X + 5) 2 +3!(X + 5) 3 +... + P!(X + 5) P +...

Soluţie .

x + 5), acestea. centru de convergenţă X 0 = - 5. Coeficientul numeric al seriei A P = n!.

Să găsim raza de convergență a seriei

.

Astfel, intervalul de convergență este format dintr-un punct - centrul intervalului de convergență x = - 5.

Exemplul 21

Găsiți aria de convergență a seriei
.

Soluţie.

Această serie este o serie de puteri în puteri ( X–2), acestea.

centru de convergenţă X 0 = 2. Rețineți că seria este semn pozitiv pentru orice fix X, deoarece expresia ( X- 2) ridicat la puterea de 2 P. Să aplicăm testul radical Cauchy la serie.

Seria va converge dacă valoarea limită este mai mică de 1, adică.

,
,
,

Aceasta înseamnă că raza de convergență
, apoi integrala de convergență

,
.

Astfel, seria converge absolut la X
. Rețineți că integrala de convergență este simetrică față de centrul de convergență X O = 2.

Să studiem convergența seriei la capetele intervalului de convergență.

crezând
, obținem o serie numerică cu semn pozitiv

Să folosim criteriul necesar pentru convergență:

prin urmare, seria de numere diverge, iar punctul
este punctul de divergenta. Rețineți că atunci când am calculat limita, am folosit a doua limită remarcabilă.

crezând
, obținem aceeași serie de numere (verificați-l singur!), ceea ce înseamnă punct
de asemenea, nu este inclusă în intervalul de convergență.

Deci, regiunea de convergență absolută a acestei serii X
.

2.3. Proprietățile serii de puteri convergente

Știm că o sumă finită de funcții continue este continuă; suma funcțiilor diferențiabile este diferențiabilă, iar derivata sumei este egală cu suma derivatelor; suma finală poate fi integrată termen cu termen.

Rezultă că pentru „sume infinite” de funcții — serii de funcții — proprietățile nu sunt valabile în cazul general.

De exemplu, luați în considerare seria funcțională

Este evident că toți termenii seriei sunt funcții continue. Să găsim regiunea de convergență a acestei serii și suma ei. Pentru a face acest lucru, găsim sumele parțiale ale seriei

apoi suma seriei

Deci suma S(X) dintr-o serie dată, ca limită a unei secvențe de sume parțiale, există și este finită pentru X (-1;1), Aceasta înseamnă că acest interval este regiunea de convergență a seriei. Mai mult, suma sa este o funcție discontinuă, deoarece

Deci, acest exemplu arată că în cazul general proprietățile sumelor finite nu au analog pentru sume infinite - serie. Totuși, pentru un caz special de serie funcțională - seria de puteri - proprietățile sumei sunt similare cu proprietățile sumelor finite.

– poate că complexul nu se va dovedi atât de complex;) Și titlul acestui articol este, de asemenea, necinstit - serialele despre care vor fi discutate astăzi nu sunt, mai degrabă, complexe, ci „pământ rar”. Cu toate acestea, chiar și studenții cu fracțiune de normă nu sunt imuni de ei și, prin urmare, această lecție aparent suplimentară ar trebui luată cu cea mai mare seriozitate. La urma urmei, după ce ai rezolvat-o, vei putea face față aproape oricărei „fiare”!

Să începem cu clasicii genului:

Exemplul 1

În primul rând, rețineți că aceasta NU este o serie de putere (Îți reamintesc că arată ca). Și, în al doilea rând, aici atrage imediat atenția valoarea, care evident nu poate fi inclusă în regiunea de convergență a seriei. Și acesta este deja un mic succes al studiului!

Dar totuși, cum să obții un mare succes? Mă grăbesc să vă mulțumesc - astfel de serii pot fi rezolvate exact în același mod ca și putere– bazat pe semnul lui d’Alembert sau semnul radical Cauchy!

Soluţie: valoarea nu este în intervalul de convergență al seriei. Acesta este un fapt semnificativ și trebuie remarcat!

Algoritmul de bază funcționează ca standard. Folosind criteriul lui d'Alembert, găsim intervalul de convergență al seriei:

Seria converge la . Să mutăm modulul în sus:

Să verificăm imediat punctul „rău”: valoarea nu este inclusă în domeniul de convergență al seriei.

Să investigăm convergența seriei la capetele „interioare” ale intervalelor:
daca atunci
daca atunci

Ambele serii de numere diferă deoarece semn necesar de convergenţă.

Răspuns: zona de convergență:

Să facem o mică verificare analitică. Să înlocuim o valoare din intervalul corect în seria funcțională, de exemplu:
– converge spre semnul lui d'Alembert.

În cazul înlocuirii valorilor din intervalul stâng, se obțin și serii convergente:
daca atunci .

Și în sfârșit, dacă , atunci seria – chiar diverge.

Câteva exemple simple de încălzit:

Exemplul 2

Găsiți aria de convergență a seriei funcționale

Exemplul 3

Găsiți aria de convergență a seriei funcționale

Fii deosebit de bun la a face față „noilor” modul– se va întâmpla de 100.500 de ori astăzi!

Scurte soluții și răspunsuri la sfârșitul lecției.

Algoritmii utilizați par a fi universali și lipsiți de probleme, dar de fapt nu este cazul - pentru multe serii funcționale, adesea „alunecă” și chiar conduc la concluzii eronate (Voi lua în considerare și astfel de exemple).

Asperitățile încep deja la nivelul interpretării rezultatelor: luați în considerare, de exemplu, seria. Aici, în limita pe care o ajungem (verificați singur), iar în teorie trebuie să dai răspunsul că seria converge într-un singur punct. Cu toate acestea, punctul este „jucat”, ceea ce înseamnă că „pacientul” nostru diverge peste tot!

Și pentru o serie, soluția „evidentă” Cauchy nu oferă absolut nimic:
– pentru ORICE valoare a lui „x”.

Și apare întrebarea, ce să faci? Folosim metoda căreia îi va fi dedicată partea principală a lecției! Poate fi formulat astfel:

Analiza directă a seriilor de numere pentru diferite valori

De fapt, am început deja să facem acest lucru în Exemplul 1. Mai întâi, examinăm un „X” specific și seria de numere corespunzătoare. Rog să luăm valoarea:
– seria numerică rezultată diverge.

Și acest lucru provoacă imediat gândul: ce se întâmplă dacă același lucru se întâmplă în alte puncte?
Sa verificam un semn necesar de convergenţă a unei serii Pentru arbitrar sensuri:

Punctul este luat în considerare mai sus, pentru toți ceilalți „X” Vom aranja ca standard a doua limită minunată:

Concluzie: seria diverge de-a lungul întregii drepte numerice

Și această soluție este cea mai viabilă opțiune!

În practică, seria funcțională trebuie adesea comparată cu serii armonice generalizate :

Exemplul 4

Soluţie: în primul rând, să ne ocupăm de domeniul definirii: în acest caz, expresia radicală trebuie să fie strict pozitivă, iar, în plus, toți termenii seriei trebuie să existe, începând de la 1. Din aceasta rezultă că:
. Cu aceste valori se obțin serii convergente condiționat:
etc.

Alte „x” nu sunt potrivite, deci, de exemplu, atunci când obținem un caz ilegal în care primii doi termeni ai seriei nu există.

Totul este bine, totul este clar, dar rămâne încă o întrebare importantă - cum să oficializezi corect decizia? Propun o schemă care poate fi numită colocvial „săgeți de traducere” în seria de numere:

Sa luam in considerare arbitrar sens și studiază convergența seriei de numere. Rutină semnul lui Leibniz:

1) Această serie este alternativă.

2) – termenii seriei scad în modul. Fiecare membru următor al seriei este mai puțin modulo decât cel anterior: , ceea ce înseamnă că scăderea este monotonă.

Concluzie: seria converge după criteriul lui Leibniz. După cum sa menționat deja, convergența aici este condiționată - din motivul că seria – diverge.

Exact așa - îngrijit și corect! Pentru că în spatele „alfa” am ascuns în mod inteligent toate seriile de numere permise.

Răspuns: seria funcţională există şi converge condiţionat la .

Un exemplu similar pentru o soluție independentă:

Exemplul 5

Investigați convergența unei serii funcționale

O mostră aproximativă a temei finale la sfârșitul lecției.

Atât pentru „ipoteza ta de lucru”! – seria funcţională converge asupra intervalului!

2) Cu un interval simetric totul este transparent, luați în considerare arbitrar valori și obținem: – serie de numere absolut convergente.

3) Și în sfârșit, „mijlocul”. Și aici este convenabil să evidențiem două lacune.

Luăm în considerare arbitrar valoare din interval și obținem o serie de numere:

! Din nou - dacă este dificil , înlocuiți un anumit număr, de exemplu . Totuși... ai vrut dificultăți =)

Efectuat pentru toate valorile „en” , Mijloace:
- astfel, conform comparaţie seria converge împreună cu o progresie infinit descrescătoare.

Pentru toate valorile lui „x” din intervalul pe care îl obținem – serie de numere absolut convergente.

Toate „X-urile” au fost explorate, nu mai există „X”-uri!

Răspuns: intervalul de convergență al seriei:

Trebuie să spun, un rezultat neașteptat! Și mai trebuie adăugat că folosirea semnelor lui d'Alembert sau Cauchy aici va fi cu siguranță înșelătoare!

Evaluarea directă este „acrobația” analizei matematice, dar aceasta, desigur, necesită experiență și, în unele cazuri, chiar intuiție.

Sau poate cineva va găsi o cale mai ușoară? Scrie! Apropo, există precedente - de mai multe ori cititorii au propus soluții mai raționale și le-am publicat cu plăcere.

O aterizare reusita :)

Exemplul 11

Găsiți aria de convergență a seriei funcționale

Versiunea mea a soluției este foarte apropiată.

Hardcore suplimentar poate fi găsit în Secțiunea VI (Rânduri) Colecția lui Kuznețov (Problemele 11-13). Există soluții gata făcute pe Internet, dar aici am nevoie de tine a avertiza– multe dintre ele sunt incomplete, incorecte sau chiar complet eronate. Și, apropo, acesta a fost unul dintre motivele pentru care s-a născut acest articol.

Să rezumăm cele trei lecții și să ne sistematizăm instrumentele. Asa de:

Pentru a găsi intervalul (intervalele) de convergență a unei serii de funcții, puteți utiliza:

1) semnul lui D'Alembert sau semnul lui Cauchy. Și dacă rândul nu este potolit– dăm dovadă de prudență sporită atunci când analizăm rezultatul obținut prin substituirea directă a diferitelor valori.

2) Testul Weierstrass pentru convergență uniformă. Nu uita!

3) Comparație cu seria numerică standard– reguli în cazul general.

Apoi examinați capetele intervalelor găsite (daca este nevoie)și obținem regiunea de convergență a seriei.

Acum aveți la dispoziție un arsenal destul de serios, care vă va permite să faceți față aproape oricărei sarcini tematice.

Vă doresc succes!

Solutii si raspunsuri:

Exemplul 2: Soluţie: valoarea nu este în intervalul de convergență al seriei.
Folosim semnul lui d'Alembert:


Seria converge la:

Astfel, intervalele de convergență ale seriei funcționale: .
Să investigăm convergența seriei la punctele finale:
daca atunci ;
daca atunci .
Ambele serii de numere diverg, deoarece nu este îndeplinit criteriul de convergenţă necesar.

Răspuns : zona de convergență: