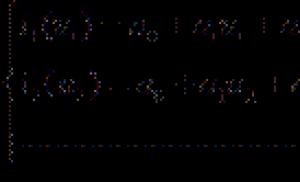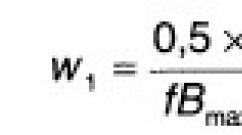Perkiraan sifat-sifat unsur nonlinier. Deskripsi diagram rangkaian Deskripsi diagram rangkaian

Seringkali diperlukan ekspresi analitik untuk karakteristik arus-tegangan elemen nonlinier. Ekspresi ini hanya dapat mewakili secara kasar karakteristik arus-tegangan, karena hukum fisika yang mengatur hubungan antara tegangan dan arus pada perangkat nonlinier tidak dinyatakan secara analitis.

Tugas perkiraan representasi analitis suatu fungsi, ditentukan secara grafis atau dengan tabel nilai, dalam batas perubahan tertentu dalam argumennya (variabel bebas) disebut perkiraan. Dalam hal ini, pertama, pilihan dibuat terhadap fungsi perkiraan, yaitu fungsi yang dengannya ketergantungan tertentu direpresentasikan secara perkiraan, dan, kedua, pilihan kriteria untuk menilai “kedekatan” ketergantungan ini dan fungsi yang mendekatinya.

Paling sering, polinomial aljabar, beberapa fungsi rasional pecahan, eksponensial dan transendental, atau sekumpulan fungsi linier (segmen garis lurus) digunakan sebagai fungsi perkiraan.

Kita asumsikan bahwa karakteristik arus-tegangan dari elemen nonlinier Saya= menyenangkan (kamu) ditentukan secara grafis, yaitu ditentukan pada setiap titik interval kamu min≤Dan≤Umaks, dan merupakan fungsi kontinu bernilai tunggal dari variabel tersebut Dan. Maka masalah representasi analitik dari karakteristik arus-tegangan dapat dianggap sebagai masalah perkiraan fungsi tertentu ξ(x) dengan fungsi perkiraan yang dipilih F(X).

Tentang kedekatannya F(X) dan perkiraan ξ( X)fungsi atau, dengan kata lain, kesalahan perkiraan, biasanya dinilai dari nilai absolut terbesar dari selisih antara fungsi-fungsi ini dalam interval perkiraan A≤ X≤ B, yaitu dalam ukuran

Δ=maks‌‌│ F(X)- ξ( X)│

Seringkali, nilai kuadrat rata-rata dari selisih antara fungsi-fungsi tertentu dalam interval perkiraan dipilih sebagai kriteria kedekatan.

Terkadang, di bawah kedekatan dua fungsi f( X) dan ξ( X) memahami kebetulan pada suatu titik tertentu

x = Ho fungsi itu sendiri dan P+ 1 turunannya.

Cara paling umum untuk memperkirakan fungsi analitik ke fungsi tertentu adalah interpolasi(metode titik-titik yang dipilih), ketika mereka mencapai kebetulan fungsi f( X) dan ξ( X) di titik-titik yang dipilih (di interpolasi) X k , k= 0, 1, 2, ..., P.

Kesalahan aproksimasi dapat dicapai semakin kecil, semakin besar jumlah parameter bervariasi yang termasuk dalam fungsi aproksimasi, yaitu, misalnya, semakin tinggi derajat polinomial aproksimasi atau semakin besar jumlah segmen lurus yang dikandung oleh aproksimasi fungsi patah linier. . Pada saat yang sama, tentu saja, volume perhitungan meningkat, baik dalam memecahkan masalah perkiraan dan dalam analisis selanjutnya dari rangkaian nonlinier. Kesederhanaan analisis ini, bersama dengan ciri-ciri fungsi aproksimasi dalam interval aproksimasi, menjadi salah satu kriteria terpenting saat memilih jenis fungsi aproksimasi.

Dalam masalah perkiraan karakteristik tegangan arus perangkat elektronik dan semikonduktor, sebagai suatu peraturan, tidak perlu mengupayakan keakuratan reproduksi yang tinggi karena penyebaran karakteristik perangkat yang signifikan dari sampel ke sampel dan pengaruh destabilisasi yang signifikan. faktor-faktornya, misalnya suhu pada perangkat semikonduktor. Dalam kebanyakan kasus, cukup dengan “dengan benar” mereproduksi sifat rata-rata ketergantungan secara keseluruhan Saya= F(kamu)dalam jangkauan operasinya. Untuk dapat menghitung secara analitis rangkaian dengan elemen nonlinier, diperlukan ekspresi matematika untuk karakteristik elemen. Karakteristik ini sendiri biasanya bersifat eksperimental, yaitu. diperoleh sebagai hasil pengukuran elemen-elemen yang sesuai, dan kemudian data referensi (tipikal) dibentuk atas dasar ini. Prosedur untuk mendeskripsikan secara matematis suatu fungsi tertentu dalam matematika disebut pendekatan fungsi ini. Ada beberapa jenis perkiraan: berdasarkan titik yang dipilih, menurut Taylor, menurut Chebyshev, dll. Pada akhirnya, perlu diperoleh ekspresi matematika yang memenuhi fungsi perkiraan awal dengan persyaratan tertentu yang ditentukan.

Mari kita pertimbangkan metode paling sederhana: metode interpolasi titik atau simpul yang dipilih dengan polinomial pangkat.

Penting untuk menentukan koefisien polinomial. Untuk tujuan ini, pilih (n+1) titik pada fungsi tertentu dan sistem persamaan dikompilasi:

Dari sistem ini koefisien-koefisiennya ditemukan a 0, a 1, a 2, …, dan n.

Pada titik yang dipilih, fungsi perkiraan akan bertepatan dengan fungsi aslinya, pada titik lain akan berbeda (sangat atau tidak - tergantung pada polinomial pangkat).

Anda dapat menggunakan polinomial eksponensial:

Metode kedua: Metode perkiraan Taylor . Dalam hal ini, satu titik dipilih di mana fungsi aslinya akan bertepatan dengan fungsi perkiraannya, tetapi kondisi tambahan ditetapkan bahwa turunannya juga bertepatan pada titik ini.

Perkiraan Butterworth: polinomial paling sederhana dipilih:

Dalam hal ini, Anda dapat menentukan deviasi maksimum ε di ujung rentang.

Perkiraan Chebyshev: adalah hukum pangkat, di mana kecocokan terjadi pada beberapa titik dan deviasi maksimum fungsi perkiraan dari fungsi aslinya diminimalkan. Dalam teori pendekatan fungsi terbukti bahwa deviasi terbesar pada nilai absolut adalah polinomial F(X)derajat P dari fungsi kontinu ξ( X) akan menjadi kemungkinan minimum jika, dalam interval pendekatan A≤ X≤ B perbedaan

F( X) - ξ( X) tidak kurang dari n + 2 waktu yang dibutuhkan berturut-turut maksimum maksimumnya F(X) - ξ( X) = L> 0 dan terkecil F(X) - ξ( X) = -L nilai (kriteria Chebyshev).

Dalam banyak masalah terapan, pendekatan polinomial menggunakan kriteria kedekatan kuadrat rata-rata digunakan, ketika parameter dari fungsi perkiraan F(X) dipilih dari kondisi putaran ke minimum dalam interval perkiraan A≤ X≤ B kuadrat deviasi fungsi F(X) dari fungsi kontinu tertentu ξ( X), yaitu dari kondisi:

Λ= 1/b-a∫ a [ F(X)- ξ( X)] 2 dx= menit. (7)

Sesuai dengan aturan mencari ekstrem, penyelesaian masalah direduksi menjadi penyelesaian sistem persamaan linier, yang terbentuk sebagai hasil menyamakan turunan parsial pertama dari fungsi tersebut dengan nol. Λ untuk setiap koefisien yang diperlukan sebuah k memperkirakan polinomial F(X), yaitu persamaan

dΛ ∕da 0=0; dΛ ∕da 1=0; dΛ ∕da 2=0, . . . , dΛ ∕da n=0. (8)

Sistem persamaan ini terbukti juga mempunyai solusi yang unik. Dalam kasus yang paling sederhana, ini ditemukan secara analitis, dan dalam kasus umum - secara numerik.

Chebyshev menetapkan bahwa persamaan berikut harus dipenuhi untuk deviasi maksimum:

Dalam praktik teknik, yang disebut pendekatan linier sepotong-sepotong adalah deskripsi kurva tertentu dengan segmen garis lurus.

Dalam setiap bagian linierisasi karakteristik arus-tegangan, semua metode untuk menganalisis osilasi dalam rangkaian listrik linier dapat diterapkan. Jelas bahwa semakin besar jumlah bagian linier yang membagi karakteristik tegangan-arus tertentu, semakin akurat perkiraannya dan semakin besar jumlah perhitungan selama analisis osilasi dalam rangkaian.

Dalam banyak masalah terapan dalam menganalisis osilasi pada rangkaian resistif nonlinier, perkiraan karakteristik arus-tegangan dalam interval perkiraan diwakili dengan akurasi yang cukup oleh dua atau tiga segmen lurus.

Perkiraan karakteristik arus-tegangan seperti itu dalam banyak kasus memberikan hasil akurasi yang cukup memuaskan untuk analisis osilasi dalam rangkaian resistif nonlinier di bawah pengaruh besaran "kecil" pada elemen nonlinier, yaitu ketika nilai arus sesaat dalam elemen nonlinier perubahan elemen dalam batas maksimum yang diizinkan dari SAYA= 0 sampai SAYA = saya berayun

(Harap perhatikan bagian tambahan tertanggal 06/04/2017 di akhir artikel.)

Akuntansi dan kontrol! Mereka yang berusia di atas 40 tahun harus mengingat dengan baik slogan era pembangunan sosialisme dan komunisme di negara kita ini.

Tetapi tanpa akuntansi yang mapan, tidak mungkin berfungsinya suatu negara, wilayah, perusahaan, atau rumah tangga secara efektif dalam pembentukan sosio-ekonomi masyarakat mana pun! Untuk menyusun prakiraan dan rencana kegiatan dan pengembangan, diperlukan data awal. Dimana saya bisa mendapatkannya? Hanya satu dapat diandalkan sumbernya adalah milikmu catatan statistik periode waktu sebelumnya.

Dalam pemahaman saya, setiap orang waras harus memperhitungkan hasil kegiatannya, mengumpulkan dan mencatat informasi, mengolah dan menganalisis data, serta menerapkan hasil analisis untuk mengambil keputusan yang tepat di masa depan. Ini tidak lebih dari akumulasi dan penggunaan pengalaman hidup seseorang secara rasional. Jika Anda tidak menyimpan catatan data penting, maka setelah jangka waktu tertentu Anda akan melupakannya dan, ketika Anda mulai menangani masalah ini lagi, Anda akan kembali melakukan kesalahan yang sama seperti yang Anda lakukan saat pertama kali melakukan ini.

“Saya ingat 5 tahun yang lalu kami memproduksi hingga 1000 buah produk semacam itu per bulan, dan sekarang kami hampir tidak dapat merakit 700 buah!” Kami membuka statistik dan melihat bahwa 5 tahun yang lalu mereka bahkan tidak memproduksi 500 buah...

“Berapa harga satu kilometer mobil Anda, dengan memperhitungkan setiap orang biaya? Mari kita buka statistiknya – 6 rubel/km. Perjalanan ke tempat kerja – 107 rubel. Lebih murah daripada naik taksi (180 rubel) lebih dari satu setengah kali lipat. Dan ada kalanya naik taksi lebih murah...

“Berapa lama waktu yang dibutuhkan untuk membuat struktur baja menara komunikasi sudut setinggi 50m?” Kami membuka statistik - dan dalam 5 menit jawabannya sudah siap...

“Berapa biaya renovasi kamar di apartemen?” Kami mengambil catatan lama, membuat penyesuaian terhadap inflasi selama beberapa tahun terakhir, memperhitungkan bahwa terakhir kali kami membeli bahan 10% lebih murah dari harga pasar dan kami sudah mengetahui perkiraan biayanya...

Dengan mencatat aktivitas profesional Anda, Anda akan selalu siap menjawab pertanyaan atasan Anda: “Kapan!!!???” Dengan menyimpan catatan rumah tangga, akan lebih mudah untuk merencanakan pengeluaran untuk pembelian dalam jumlah besar, liburan, dan pengeluaran lainnya di masa depan, mengambil tindakan yang tepat untuk memperoleh penghasilan tambahan atau mengurangi pengeluaran yang tidak perlu saat ini.

Pada artikel ini, saya akan menggunakan contoh sederhana untuk menunjukkan bagaimana data statistik yang dikumpulkan dapat diproses di Excel untuk digunakan lebih lanjut dalam memperkirakan periode mendatang.

Perkiraan data statistik di Excel dengan fungsi analitis.

Tempat produksi memproduksi struktur logam bangunan dari produk logam lembaran dan profil. Situs beroperasi secara stabil, jenis pesanannya sama, jumlah pekerja sedikit berfluktuasi. Terdapat data keluaran produk selama 12 bulan sebelumnya dan jumlah logam canai yang diproses selama periode waktu tersebut berdasarkan kelompok: lembaran, balok I, saluran, sudut, pipa bundar, profil persegi panjang, produk bulat. Setelah analisis awal terhadap data awal, muncul asumsi bahwa total produksi bulanan struktur logam sangat bergantung pada jumlah sudut pesanan. Mari kita periksa asumsi ini.

Pertama-tama, beberapa kata tentang perkiraan. Kita akan mencari hukum - fungsi analitik, yaitu fungsi yang ditentukan oleh persamaan yang menggambarkan ketergantungan total output struktur logam pada jumlah baja sudut dalam pesanan yang diselesaikan lebih baik daripada yang lain. Ini adalah perkiraan, dan persamaan yang ditemukan disebut fungsi perkiraan untuk fungsi aslinya, diberikan dalam bentuk tabel.

1. Nyalakan Excel dan letakkan tabel dengan data statistik pada selembar kertas.

2. Selanjutnya, kita membuat dan memformat plot pencar, di mana sepanjang sumbu X kita menetapkan nilai argumen - jumlah sudut yang diproses dalam ton. Sepanjang sumbu Y kami memplot nilai fungsi asli - total produksi struktur logam per bulan, yang ditentukan dalam tabel.

3. Kami “mengarahkan” mouse ke salah satu titik pada grafik dan klik kanan untuk membuka menu konteks (seperti yang dikatakan salah satu teman baik saya - saat bekerja di program asing, saat Anda tidak tahu harus berbuat apa, klik tombol kanan mouse lebih sering...). Di menu tarik-turun, pilih “Tambahkan garis tren…”.

4. Di jendela “Garis Tren” yang muncul, pada tab “Jenis”, pilih “Linear”.

6. Sebuah garis lurus muncul pada grafik, mendekati ketergantungan tabel kita.

Selain garis itu sendiri, kita melihat persamaan garis ini dan, yang terpenting, kita melihat nilai parameter R 2 - nilai reliabilitas pendekatan! Semakin dekat nilainya dengan 1, semakin akurat fungsi yang dipilih mendekati data tabel!

7. Kita membuat garis tren menggunakan pendekatan pangkat, logaritmik, eksponensial, dan polinomial dengan cara yang sama seperti kita membuat garis tren linier.

Dari semua fungsi yang dipilih, polinomial derajat kedua paling mendekati data kita; polinomial tersebut memiliki koefisien reliabilitas maksimum R 2 .

Namun, saya ingin memperingatkan Anda! Jika Anda mengambil polinomial dengan derajat yang lebih tinggi, Anda mungkin akan mendapatkan hasil yang lebih baik lagi, namun kurvanya akan terlihat berbelit-belit... Penting untuk dipahami di sini bahwa kita mencari fungsi yang memiliki arti fisik. Apa artinya ini? Ini berarti bahwa kita memerlukan fungsi perkiraan yang akan memberikan hasil yang memadai tidak hanya dalam rentang nilai X yang dipertimbangkan, tetapi juga di luar rentang tersebut, yaitu, fungsi tersebut akan menjawab pertanyaan: “Berapa keluaran struktur logam jika jumlah sudut yang diproses per bulan kurang dari 45 dan lebih dari 168 ton! Oleh karena itu, saya tidak menyarankan untuk terbawa oleh polinomial derajat tinggi, dan memilih parabola (polinomial derajat kedua) dengan hati-hati!

Jadi, kita perlu memilih fungsi yang tidak hanya menginterpolasi data tabel dengan baik dalam rentang nilai X = 45...168, tetapi juga memungkinkan ekstrapolasi yang memadai di luar rentang ini. Dalam hal ini, saya memilih fungsi logaritma, meskipun Anda juga dapat memilih fungsi linier, karena ini yang paling sederhana. Dalam contoh yang sedang dipertimbangkan, ketika memilih pendekatan linier di Excel, kesalahannya akan lebih besar daripada ketika memilih pendekatan logaritmik, tetapi tidak banyak.

8. Kami menghapus semua garis tren dari bidang grafik, kecuali fungsi logaritma. Untuk melakukan ini, klik kanan pada baris yang tidak perlu dan pilih “Hapus” dari menu konteks yang muncul.

9. Terakhir, kami akan menambahkan bilah kesalahan ke titik data tabel. Untuk melakukan ini, klik kanan pada salah satu titik pada grafik dan pilih “Format seri data…” di menu konteks dan konfigurasikan data pada tab “Kesalahan Y” seperti pada gambar di bawah.

10. Kemudian klik kanan pada salah satu garis rentang kesalahan, pilih “Format bilah kesalahan…” di menu konteks dan di jendela “Format bilah kesalahan” pada tab “Tampilan”, sesuaikan warna dan ketebalan garis.

Objek diagram lainnya diformat dengan cara yang sama.Unggul!

Hasil akhir grafik ditunjukkan pada tangkapan layar berikut.

Hasil.

Hasil dari semua tindakan sebelumnya adalah rumus yang dihasilkan untuk fungsi aproksimasi y=-172.01*ln (x)+1188.2. Mengetahui hal ini, dan jumlah sudut dalam rangkaian pekerjaan bulanan, dengan tingkat probabilitas yang tinggi (±4% - lihat bilah kesalahan) dimungkinkan untuk memprediksi total produksi struktur logam pada bulan tersebut! Misalnya, jika rencana untuk satu bulan adalah 140 ton sudut, maka total output, jika semua hal lain dianggap sama, kemungkinan besar adalah 338 ± 14 ton.

Untuk meningkatkan keandalan perkiraan, harus ada banyak data statistik. Dua belas pasang nilai saja tidak cukup.

Dari praktik, saya akan mengatakan bahwa menemukan fungsi perkiraan dengan koefisien reliabilitas R 2 >0,87 harus dianggap sebagai hasil yang baik. Hasil yang sangat baik adalah dengan R 2 >0,94.

Dalam praktiknya, mungkin sulit untuk mengidentifikasi satu faktor penentu terpenting (dalam contoh kita, massa sudut yang diproses dalam sebulan), namun jika Anda mencobanya, Anda selalu dapat menemukannya di setiap tugas tertentu! Tentu saja, total output selama sebulan sangat bergantung pada ratusan faktor, yang memerlukan biaya tenaga kerja yang signifikan dari pembuat standar dan spesialis lainnya. Tapi hasilnya masih perkiraan! Jadi, apakah layak mengeluarkan biaya ketika ada pemodelan matematika yang jauh lebih murah!

Dalam artikel ini, saya hanya menyentuh puncak gunung es yang disebut pengumpulan, pengolahan, dan penggunaan praktis data statistik. Saya berharap dapat mengetahui apakah saya berhasil atau tidak membangkitkan minat Anda terhadap topik ini dari komentar dan penilaian artikel di mesin pencari.

Isu yang diangkat tentang pendekatan suatu fungsi suatu variabel memiliki penerapan praktis yang luas dalam berbagai bidang kehidupan. Namun solusi terhadap masalah perkiraan fungsi memiliki penerapan yang jauh lebih besar beberapa independen variabel... Baca tentang ini dan lebih banyak lagi di artikel blog berikut.

Langganan untuk pengumuman artikel di jendela yang terletak di akhir setiap artikel atau di jendela di bagian atas halaman.

Jangan lupa mengonfirmasi berlangganan dengan mengklik tautan dalam surat yang akan datang kepada Anda melalui surat yang ditentukan (mungkin sampai di folder « Spam » )!!!

Saya akan membaca komentar Anda dengan penuh minat, para pembaca yang budiman! Menulis!

P.S. (06/04/2017)

Penggantian data tabel yang sangat akurat dan indah dengan persamaan sederhana.

Anda tidak puas dengan akurasi perkiraan yang diperoleh (R 2<0,95) или вид и набор функций, предлагаемые MS Excel?

Apakah dimensi ekspresi dan bentuk garis mendekati polinomial derajat tinggi tidak enak dipandang?

Silakan merujuk ke halaman "" untuk mendapatkan hasil perkiraan data tabel Anda yang lebih akurat dan ringkas dan untuk mempelajari teknik sederhana untuk menyelesaikan masalah perkiraan presisi tinggi dengan fungsi satu variabel.

Saat menggunakan algoritme tindakan yang diusulkan, ditemukan fungsi yang sangat kompak yang memberikan akurasi perkiraan tertinggi: R 2 =0,9963!!!

Perkiraan fungsi nonlinier

x 0 /12 /6 /4 /3 5/12 /2

kamu 0,5 0,483 0,433 0,354 0,25 0,129 0

Karena interval pembagian fungsi adalah sama, kami menghitung koefisien kemiringan berikut dari bagian-bagian yang sesuai dari fungsi yang didekati:

1. Konstruksi balok untuk membentuk segmen fungsi aproksimasi

Pembentukan fungsi waktu

Ubah interval:

Waktu mulai ulang siklik: T = 1 detik

Sekarang mari kita modelkan fungsinya:

Perkiraan

Gambar 3.1 - Skema penyelesaian persamaan

Gambar 3.2 - Diagram blok pembentukan fungsi nonlinier

Dengan demikian, ruas kiri persamaan otomatis terbentuk. Dalam hal ini, secara konvensional diasumsikan bahwa turunan tertinggi x// diketahui, karena suku-suku di sisi kanan persamaan diketahui dan dapat dihubungkan ke input U1 (Gambar 3.1). Penguat operasional U3 bertindak sebagai inverter sinyal +x. Untuk mensimulasikan x//, perlu memasukkan subamplifier lain ke dalam rangkaian, yang inputnya perlu disuplai sinyal yang mensimulasikan sisi kanan persamaan (3.2).

Skala semua variabel dihitung dengan mempertimbangkan bahwa nilai maksimum variabel mesin di luar nilai absolut adalah 10 V:

Mx = 10 / xmaks; Mx/ = 10 / x/ maks; Mx // = 10 / x //maks;

Saya = 10 / ymax. (3.3)

Skala waktu Mt = T / tmax = 1, karena permasalahan disimulasikan secara real time.

Koefisien transmisi untuk setiap input penguat integrasi dihitung.

Untuk penguat U1, koefisien transmisi dicari dengan menggunakan rumus:

K11 = Mx/ b / (MyMt); K12 = Mx/ a2 / (MxMt);

K13 = Mx/ a1 / (MxMt). (3.4)

Untuk penguat U2:

K21 = Mx/ / (Mx/ Mt), (3,5)

dan untuk penguat U3:

K31 = 1.(3.6)

Tegangan kondisi awal dihitung menggunakan rumus:

ux/ (0) = Mx/ x/ (0) (-1); ux(0)= Mxx(0) (+1). (3.7)

Ruas kanan persamaan (3.2) diwakili oleh fungsi nonlinier, yang ditentukan dengan pendekatan linier. Dalam hal ini, perlu untuk memeriksa bahwa kesalahan perkiraan tidak melebihi nilai yang ditentukan. Diagram blok pembentukan fungsi nonlinier disajikan pada Gambar 3.2.

Deskripsi diagram sirkuit

Blok pembangkit fungsi waktu (Ф) dibuat dalam bentuk satu (membentuk t) atau dua penguat terintegrasi seri (membentuk t2) dengan kondisi awal nol.

Dalam hal ini, ketika sinyal U diterapkan ke masukan integrator pertama, pada keluarannya kita memperoleh:

u1(t)= - K11 = - K11Et. (3.8)

Dengan menempatkan K11E=1, kita mendapatkan u1(t)= t.

Pada keluaran integrator kedua kita mendapatkan:

u2(t)= K21 = K11K21Et2 / 2 (3,9)

Mengatur K11K21E/2 = 1, kita mendapatkan u2(t)= t2.

Blok untuk membentuk segmen fungsi aproksimasi diimplementasikan dalam bentuk blok dioda fungsi nonlinier (DBNF), yang nilai inputnya merupakan fungsi waktu t atau t2. Prosedur untuk menghitung dan membangun DBNF diberikan dalam.

Penambah (SAD) segmen fungsi aproksimasi dilakukan dalam bentuk penguat akhir diferensial.

Kondisi awal untuk integrator rangkaian pemodelan diperkenalkan menggunakan node dengan struktur variabel (Gambar 3.3). Skema ini dapat beroperasi dalam dua mode:

a) integrasi - dengan kunci K di posisi 1. Dalam hal ini, sinyal awal rangkaian digambarkan dengan cukup akurat melalui persamaan integrator ideal:

u1(t)= - (1 / RC) . (3.10)

Mode ini digunakan saat memodelkan suatu tugas. Untuk memeriksa kebenaran pilihan parameter R dan C integrator, periksa nilai tegangan awal integrator sebagai fungsi waktu dan waktu integrasi yang berguna dalam kesalahan yang diizinkan?

Besarnya tegangan integrator awal

U(t)= - KYE (1 - e - T / [(Ky+1)RC) (3.11)

selama simulasi, T ketika mengintegrasikan sinyal input E menggunakan penguat operasional dengan penguatan Ky tanpa rangkaian umpan balik tidak boleh melebihi nilai variabel mesin (10 V).

Waktu integrasi

Ti = 2RC(Kу + 1)?Uadd (3.12)

dengan parameter rangkaian yang dipilih tidak boleh kurang dari waktu simulasi T.

b) pengaturan kondisi awal diterapkan ketika kunci K dialihkan ke posisi 2. Mode ini digunakan ketika mempersiapkan rangkaian pemodelan untuk proses solusi. Dalam hal ini, sinyal asli rangkaian dijelaskan dengan persamaan:

u0(t)= - (R2 /R1) E (3.13)

dimana u0(t) adalah nilai kondisi awal.

Untuk mengurangi waktu pembentukan kondisi awal dan memastikan pengoperasian yang andal, parameter rangkaian harus memenuhi kondisi: R1C1 = R2C.

Buatlah skema perhitungan yang lengkap. Dalam hal ini, Anda harus menggunakan simbol yang diberikan pada subbagian 3.1.

Dengan menggunakan kedalaman bit data masukan dan sumber, buat diagram sirkuit blok B1 dan B2 dan sambungkan ke blok RS.

Perkiraan fungsi

Perkenalan

Ketika sampel data eksperimen diproses, sampel tersebut paling sering disajikan sebagai larik yang terdiri dari pasangan angka (x saya, kamu saya ). Oleh karena itu, timbul masalah dalam memperkirakan ketergantungan diskrit y(x Saya ) fungsi kontinu f(x).

Perkiraan (perkiraan) suatu fungsi adalah penemuan fungsi tersebut (fungsi perkiraan) , yang mendekati yang diberikan.

Fungsi f(x), bergantung pada spesifikasi masalahnya, dapat memenuhi berbagai persyaratan.

• Fungsi f(x) harus melalui titik (x saya ,y saya ), yaitu f(x saya )=y saya ,saya=1...n. Dalam hal ini yang mereka bicarakan interpolasi diberikan oleh fungsi f(x) di titik dalam antara x Saya , atau ekstrapolasi di luar interval yang memuat semua x Saya.
• Fungsi f(x) harus dalam beberapa hal (misalnya, dalam bentuk ketergantungan analitis tertentu) mendekati y(x Saya ), belum tentu melalui titik (x saya, kamu saya ). Ini adalah pernyataan masalahnya regresi , yang dalam banyak kasus juga bisa disebut perataan data.
• Fungsi f(x) harus mendekati ketergantungan eksperimental y(x Saya ), apalagi, dengan mempertimbangkan bahwa data (x saya, kamu saya ) diperoleh dengan kesalahan tertentu yang menyatakan komponen kebisingan dari pengukuran. Dalam hal ini, fungsi f(x), dengan menggunakan satu atau beberapa algoritma, mengurangi kesalahan yang ada pada data (x saya, kamu saya ). Jenis tugas ini disebut tugas pemfilteran. Penghalusan adalah kasus khusus pemfilteran.

Kriteria kesamaan fungsi dan mungkin berbeda.

Dalam kasus dimana perkiraan didasarkan pada himpunan titik-titik yang berlainan, maka perkiraan tersebut disebut titik atau diskrit.

Dalam hal aproksimasi dilakukan pada himpunan titik (segmen) yang kontinu, aproksimasi tersebut disebut kontinu atau integral . Contoh pendekatan tersebut adalah perluasan suatu fungsi menjadi deret Taylor, yaitu penggantian fungsi tertentu dengan polinomial pangkat.

Jenis pendekatan titik yang paling umum adalah interpolasi (dalam arti luas).

Biarkan himpunan titik-titik tertentu diberikan, disebutnode interpolasi, dan di antara titik-titik tersebut tidak ada yang bertepatan, begitu pula nilai fungsi pada titik-titik tersebut. Anda perlu membangun suatu fungsi, melewati semua node yang diberikan. Jadi, kriteria kedekatan suatu fungsi adalah.

Fungsi tersebut biasanya dipilih menjadi polinomial, yang disebutpolinomial interpolasi.

Jika polinomialnya sama untuk seluruh area interpolasi, dikatakan interpolasi global

Dalam kasus di mana polinomial berbeda antara node yang berbeda, kita bicarakan sepotong-sepotong atau interpolasi lokal.

Setelah menemukan polinomial interpolasi, kita dapat menghitung nilai fungsi antar node (lakukaninterpolasi dalam arti sempit), dan juga menentukan nilai fungsi bahkan di luar interval yang ditentukan (lakukan ekstrapolasi).

Berbagai jenis konstruksi perkiraan ketergantungan f(x) diilustrasikan pada Gambar. 1. Di atasnya, data asli ditunjukkan dengan lingkaran, interpolasi dengan segmen garis lurus ditunjukkan dengan garis putus-putus, regresi linier ditunjukkan dengan garis lurus miring, dan pemfilteran ditunjukkan dengan kurva halus yang tebal.

Beras. 1. Jenis konstruksi ketergantungan aproksimasi

Interpolasi dan ekstrapolasi

Sejumlah besar metode numerik menggunakan algoritma interpolasi. Secara umum, matematika komputasi adalah ilmu representasi fungsi diskrit. Ini adalah himpunan nilai berhingga y(x Saya ) mewakili abstraksi matematika dalam bahasa komputer - fungsi kontinu y(x). Tugas menginterpolasi fungsi satu variabel adalah mengganti ketergantungan diskrit y(x Saya ), yaitu N pasang bilangan (x saya, kamu saya ), atau, dengan kata lain, node, dengan beberapa fungsi kontinu y(x). Dalam hal ini syarat utamanya adalah fungsi y(x) harus melalui titik (x saya ,y saya ), yaitu y(x saya )=y saya ,i=1...N, serta kemampuan untuk menghitung nilai y(x) di setiap titik yang terletak di antara node.

Beras. 2. Konstruksi ketergantungan interpolasi dan ekstrapolasi.

Ketika nilai y(x) yang diinginkan dihitung pada titik x yang berada di antara salah satu node x i, bicara tentang interpolasi , dan ketika titik x terletak di luar batas interval termasuk semua x i - tentang ekstrapolasi fungsi y(x).

Pada Gambar. 2 pada sekumpulan titik (x saya, kamu saya ), ditandai dengan lingkaran, baik fungsi interpolasi (untuk x>100) maupun fungsi ekstrapolasi (untuk x<100). Интерполяция-экстраполяция показаны на рис. сплошной кривой.

Perlu diingat bahwa akurasi ekstrapolasi biasanya sangat rendah.

Untuk mengekstrapolasi data dalam masing-masing versi paket, gunakan fungsi ini prediksi (v, m ,n) . Ini menghasilkan vektor nilai prediksi berdasarkan M elemen vektor berturut-turut ay.

Parameter fungsi prediksi (v, m ,n ) : v adalah vektor yang nilainya mewakili sampel yang diambil pada interval yang sama, m dan n adalah bilangan bulat.

Jadi "fungsi prediktif" prediksi (v, m ,n) menggunakan data yang ada untuk memprediksi data baru yang berada di luar cakupan tugas. Ia menggunakan algoritma prediksi linier, yang cukup bila fungsinya mulus atau bergantian, meski tidak harus periodik.

Contoh di bawah mengilustrasikan penggunaan prediksi linier.

7 .1 Interpolasi lokal

7 .1.1. Interpolasi linier

Kasus interpolasi lokal yang paling sederhana adalah interpolasi linier, ketika polinomial derajat pertama dipilih sebagai fungsi interpolasi, yaitu titik-titik nodal dihubungkan oleh garis lurus.

Interpolasi linier merepresentasikan ketergantungan yang diinginkan y(x) dalam bentuk garis putus-putus. Fungsi interpolasi y(x) terdiri dari ruas-ruas garis yang menghubungkan titik-titik (x saya ,y saya ) (lihat Gambar 3).

Gambar.3 Interpolasi linier

Untuk membangun interpolasi linier, cukup pada setiap interval (x saya ,x saya+1 ) hitung persamaan garis yang melalui dua titik berikut:

Dengan interpolasi linier sepotong-sepotong, poin tambahan dihitung menggunakan hubungan linier. Secara grafis, ini berarti menghubungkan titik-titik nodal dengan segmen garis lurus.Interpolasi linier aktif matematika Ini tidak dilakukan dengan menggunakan fungsi bawaan linterp.

linterp(VX, VY, x)

Untuk vektor tertentu VX dan VY titik jangkar dan argumen yang diberikan x linterp mengembalikan nilai suatu fungsi ketika diinterpolasi secara linier. Ekstrapolasi menggunakan segmen garis yang ditarik melalui dua titik ekstrim.

Misalkan perlu dilakukan interpolasi linier terhadap fungsi sin( X ) pada interval menggunakan lima node interpolasi, dan menghitung nilai fungsi di empat titik Xk:

Atur interval perubahan X dan jumlah titik nodal

Menentukan langkah perubahan X:

Kami menghitung koordinat node dan nilai fungsi di dalamnya:

Kami melakukan interpolasi linier:

Mari kita hitung nilai fungsi interpolasi pada titik tertentu dan bandingkan dengan nilai eksaknya

Seperti yang Anda lihat, hasil interpolasi sedikit berbeda dari nilai pasti fungsinya.

7 .1.2. Interpolasi spline

Saat ini, di antara metode interpolasi lokal, interpolasi spline (dari kata bahasa Inggris spline penggaris fleksibel).

Dalam sebagian besar penerapan praktis, diinginkan untuk menghubungkan titik-titik eksperimen (x saya, kamu saya ) bukan garis putus-putus, melainkan kurva mulus. Interpolasi y(x) dengan spline kuadrat atau kubik, yaitu segmen parabola kuadrat atau kubik (lihat Gambar 4), paling cocok untuk tujuan ini.

Dalam hal ini, polinomial interpolasi derajat ketiga dibangun, melewati semua node tertentu dan memiliki turunan pertama dan kedua yang kontinu.

Gbr.4 Interpolasi spline

Pada setiap interval, fungsi interpolasinya adalah polinomial derajat ketiga

dan memenuhi persyaratan.

Jika hanya ada n node, lalu interval. Ini berarti perlu untuk menentukan koefisien polinomial yang tidak diketahui. Kondisi memberi kita N persamaan. Kondisi kontinuitas fungsi dan dua turunan pertamanya pada titik dalam interval memberikan persamaan tambahan

Secara total kami memiliki persamaan yang berbeda. Kedua persamaan yang hilang dapat diperoleh dengan menentukan kondisi pada tepi interval. Secara khusus, seseorang dapat memerlukan kelengkungan nol dari fungsi tersebut pada tepi interval, yaitu. Dengan menentukan kondisi berbeda di ujung interval, Anda bisa mendapatkan spline berbeda.

Untuk menerapkan pendekatan spline MatematikaCAD menawarkan empat fungsi bawaan. Tiga diantaranya digunakan untuk memperoleh vektor turunan kedua fungsi spline dengan berbagai jenis interpolasi:

cspIine(VX, VY) mengembalikan vektor VS turunan kedua dimendekati polinomial kubik pada titik acuan;

pspline(VX, VY) mengembalikan vektor VS turunan kedua ketika mendekati titik acuan kurva parabola;

lspline(VX, VY) mengembalikan vektor VS turunan kedua ketika mendekati titik acuan garis.

Terakhir, fungsi keempat

interp (VS, VX, VY, x)

mengembalikan nilai y(x) untuk vektor yang diberikan VS, VX, VY dan nilai tertentu x.

Dengan demikian, pendekatan spline dilakukan dalam dua tahap. Yang pertama menggunakan salah satu fungsi cspline, pspline, atau lspline vektor turunan kedua dari fungsi y(x) yang didefinisikan oleh vektor-vektor tersebut ditemukan VX dan VY nilainya (absis dan ordinat). Kemudian, pada tahap kedua, nilai y(x) dihitung untuk setiap titik yang diinginkan menggunakan fungsi tersebut interp.

Mari kita selesaikan masalah interpolasi sinus menggunakan splines melalui fungsinya interp(VS,x,y,z) . Variabel x dan y tentukan koordinat titik nodal, z adalah argumen fungsi, VS menentukan jenis kondisi batas di ujung interval.

Mari kita definisikan fungsi interpolasi untuk tiga jenis spline kubik

Kami menghitung nilai fungsi interpolasi pada titik tertentu dan membandingkan hasilnya dengan nilai eksak

Perlu dicatat bahwa hasil interpolasi dengan berbagai jenis spline kubik praktis sama pada titik-titik internal interval dan bertepatan dengan nilai eksak fungsinya. Di dekat tepi interval, perbedaannya menjadi lebih terlihat, dan ketika diekstrapolasi melampaui interval tertentu, jenis spline yang berbeda memberikan hasil yang berbeda secara signifikan. Untuk lebih jelasnya, hasilnya disajikan dalam grafik (Gbr. 5).

Gambar.5 Perbandingan interpolasi spline

Demikian pula, Anda dapat memastikan bahwa turunan pertama dan kedua dari spline adalah kontinu (Gbr. 6).

Gbr.6 Perbandingan interpolasi spline turunan (1 dan 2).

P turunan dari orde yang lebih tinggi tidak lagi berkelanjutan.

7.1.3. Interpolasi dengan B-splines

Gbr.7 Interpolasi dengan B-splines

Jenis interpolasi yang sedikit lebih kompleks adalah apa yang disebut interpolasi spline polinomial, atauInterpolasi B-spline. Berbeda dengan interpolasi spline konvensional, penggabungan spline B dasar tidak dilakukan pada titik (t saya,x saya ), dan di titik lain yang biasanya koordinatnya diminta ditentukan oleh pengguna. Oleh karena itu, tidak ada persyaratan bagi node untuk mengikuti secara seragam saat melakukan interpolasi dengan B-splines, dan node tersebut dapat memperkirakan data yang tersebar.

Spline dapat berupa polinomial derajat pertama, kedua, atau ketiga (linier, kuadrat, atau kubik). Interpolasi B-spline digunakan dengan cara yang sama seperti interpolasi spline biasa, perbedaannya hanya pada pendefinisian fungsi bantu koefisien spline.

bspline(vx, vy, u, n) Mengembalikan vektor yang berisi koefisien spline derajat B n untuk data itu berada dalam vektor vx dan vy (dengan mempertimbangkan nilai node, yang ditentukan dalam kamu) . Vektor yang dikembalikan menjadi argumen pertama dari fungsi tersebut interp.

interp (vs, vx, vy, x) Mengembalikan B - spline kuantitas yang diinterpolasi vy di titik x, dimana vs hasil dari fungsinya bspline.

Argumen

v x x .

vy y vx.

kamu - vektor nyata dengan jumlah elemen n-1 lebih sedikit dari pada vx (di mana n adalah 1, 2, atau 3). Elemen kamu harus dalam urutan menaik. Elemen berisi nilai simpul untuk interpolasi. Elemen pertama di u harus lebih kecil atau sama dengan elemen pertama di vx . Elemen terakhir pada u harus lebih besar atau sama dengan elemen terakhir pada x.

N - bilangan bulat sama dengan 1, 2, atau 3, yang menunjukkan derajat linier sepotong-sepotong(n=1) , - kuadrat(n=2) , atau kubik(n=3) polinomial masing-masing.

vs - vektor terbentuk bspline.

X - nilai variabel independen yang ingin Anda interpolasi hasilnya. Untuk hasil terbaik, itu harus berada dalam interval di mana nilai awal x ditentukan.

B - spline interpolasi memungkinkan Anda mentransfer kurva melalui sekumpulan titik. Kurva ini dibangun pada tiga titik yang berdekatan berdasarkan polinomial derajat N dan melewati titik-titik ini. Polinomial-polinomial ini digabungkan pada titik-titiknya untuk membentuk kurva yang lengkap.

7 .2. Interpolasi global

Dengan interpolasi global, satu polinomial dicari untuk seluruh interval. Jika di antara node ( x saya, kamu saya ) tidak ada yang bertepatan, maka polinomial tersebut akan unik, dan derajatnya tidak akan melebihi N.

Mari kita tulis sistem persamaan untuk menentukan koefisien polinomial

Mari kita definisikan matriks koefisien sistem persamaan

Mari kita selesaikan sistem persamaan menggunakan metode matriks

Mari kita definisikan polinomial interpolasi

Mari kita hitung nilai polinomial interpolasi pada titik tertentu dan bandingkan dengan nilai eksaknya

Koefisien polinomial interpolasi adalah sebagai berikut:

Untuk lebih jelasnya, hasilnya disajikan dalam grafik (Gbr. 8).

Catatan.

Karena akumulasi kesalahan komputasi (kesalahan pembulatan) dengan jumlah node yang banyak (n>10), penurunan tajam dalam hasil interpolasi mungkin terjadi. Selain itu, untuk sejumlah fungsi, interpolasi global dengan polinomial tidak memberikan hasil yang memuaskan sama sekali. Mari kita lihat dua fungsi tersebut sebagai contoh. Untuk fungsi ini, akurasi interpolasi tidak meningkat seiring bertambahnya jumlah node, namun menurun.

Beras. 8. Interpolasi global berdasarkan fungsi polinomial dosa(z).

Contoh selanjutnya adalah sebuah fungsi. Untuk itu, polinomial interpolasi dibuat pada interval [1;1], 9 poin digunakan.

Hasilnya disajikan pada grafik Gambar. 9.

Beras. 9 Interpolasi global dengan fungsi polinomial.

Untuk fungsinya, kita mencari polinomial interpolasi menggunakan titik-titik yang ditentukan di atas.

Hasilnya disajikan pada grafik Gambar. 10.

Beras. 10 Interpolasi global dengan fungsi polinomial.

Ketika jumlah node interpolasi bertambah, hasil interpolasi di dekat ujung interval menurun.

7 .3 Metode kuadrat terkecil

Metode yang paling umum untuk memperkirakan data eksperimen adalah metode kuadrat terkecil. Metode ini memungkinkan Anda untuk menggunakan fungsi perkiraan jenis apa pun dan termasuk dalam kelompok metode global. Versi paling sederhana dari metode kuadrat terkecil adalah perkiraan dengan garis lurus (polinomial derajat pertama). Versi metode kuadrat terkecil ini juga disebut regresi linier.

Kriteria kedekatan dalam metode kuadrat terkecil adalah persyaratan bahwa jumlah deviasi kuadrat dari fungsi aproksimasi ke titik eksperimen harus minimal:

Oleh karena itu, fungsi perkiraan tidak harus melewati semua titik tertentu, yang terutama penting ketika memperkirakan data yang jelas-jelas mengandung kesalahan.

Fitur penting dari metode ini adalah bahwa fungsi perkiraan dapat berubah-ubah. Jenisnya ditentukan oleh ciri-ciri masalah yang dipecahkan, misalnya dengan pertimbangan fisika jika hasil percobaan fisika didekati. Yang paling umum adalah perkiraan dengan garis lurus (regresi linier), perkiraan dengan polinomial (regresi polinomial), perkiraan dengan kombinasi linier dari fungsi arbitrer. Selain itu, masalah dapat direduksi menjadi masalah linier dengan mengganti variabel (melakukan linierisasi). Misalnya, biarkan fungsi perkiraan dicari dalam formulir. Mari kita ambil logaritma ungkapan ini dan perkenalkan notasinya, . Kemudian, dalam notasi baru, masalahnya direduksi menjadi mencari koefisien fungsi linier.

7 .3.1. Perkiraan fungsi linier

Mari kita terapkan metode kuadrat terkecil untuk memperkirakan data eksperimen.

Data dibaca dari file datax dan datay

Saat menggunakan MathCAD, nama file harus diapit tanda kutip dan ditulis sesuai aturan MS DOS, misalnya READPRN("c:\mylib\datax.prn").

Jumlah data yang dibaca (jumlah titik percobaan) ditentukan.

Di masa depan, fungsi bawaan digunakan kemiringan dan intersepsi untuk menentukan koefisien regresi linier (pendekatan data dengan garis lurus).

Kemiringan fungsi (vx, vy) menentukan kemiringan garis, dan fungsinya mencegat(vx, vy) titik potong grafik dengan sumbu vertikal.

matematika 2000 menyarankan penggunaan fungsi tersebut untuk tujuan yang sama garis(vx, vy) , yang membentuk vektor (elemen pertama adalah kemiringan garis, elemen kedua adalah titik potong dengan sumbu vertikal).

Argumen

vx adalah vektor nilai data nyata dalam urutan menaik. Mereka sesuai dengan nilai-nilainya X.

vy - vektor nilai data nyata. Mereka sesuai dengan nilai-nilainya kamu . Berisi jumlah elemen yang sama dengan vx.

Koefisien regresi linier

Deviasi standar adalah:

Beras. 11. Pendekatan dengan fungsi linier.

7 .3.2. Perkiraan dengan polinomial.

Untuk perkiraandata eksperimentalfungsi bawaan berfungsi sebagai polinomial derajat kedua dan ketiga regresi dan fungsinya sudah tidak asing lagi bagi kita interp . (Tentunya, jika kita mengambil polinomial berderajat satu yang lebih kecil dari jumlah titik sebagai fungsi aproksimasi, maka permasalahannya akan direduksi menjadi masalah interpolasi global dan polinomial yang dihasilkan akan melewati semua titik tertentu secara tepat.)

Kami memperkenalkan derajat polinomial:

Kemunduran fungsi (vx, vy, k) bersifat tambahan, ia menyiapkan data yang diperlukan agar fungsi dapat berfungsi interp.

Argumen

vx adalah vektor nilai data nyata dalam urutan menaik. Mereka sesuai dengan nilai-nilainya X.

vy - vektor nilai data nyata. Mereka sesuai dengan nilai-nilainya kamu . Berisi jumlah elemen yang sama dengan vx,

k adalah derajat polinomial.

Vektor vs berisi, antara lain, koefisien polinomial

fungsi interp (vs, vx, vy, z) mengembalikan polinomial dari nilai yang diinterpolasi vy di titik z, dimana vs hasil dari fungsinya regresi.

Mendefinisikan fitur baru f2, f3 , kita mendapat kesempatan untuk mencari nilai polinomial pada titik tertentu:

dan juga koefisiennya:

Simpangan baku hampir tidak dapat dibedakan satu sama lain, koefisien pangkat empat z kecil, sehingga peningkatan derajat polinomial lebih lanjut tidak tepat dan cukup membatasi diri kita hanya pada pangkat kedua.

fungsi regresi tidak tersedia di semua versi Matcad "a. Namun, regresi polinomial dapat dilakukan tanpa menggunakan fungsi ini. Untuk melakukannya, Anda perlu menentukan koefisien sistem normal dan menyelesaikan sistem persamaan yang dihasilkan, misalnya menggunakan metode matriks.

Sekarang kita akan mencoba memperkirakan data eksperimen dengan derajat polinomial m dan m1, tanpa menggunakan fungsi bawaan regresi.

Kami menghitung elemen matriks koefisien sistem normal

dan kolom anggota gratis

Kami menemukan koefisien polinomial dengan menyelesaikan sistem menggunakan metode matriks,

Mendefinisikan fungsi perkiraan

Koefisien polinomialnya adalah sebagai berikut:

Beras. 12. Pendekatan dengan polinomial derajat 2 dan 3.

fungsi regresi membuat satu polinomial aproksimasi, yang koefisiennya dihitung pada seluruh himpunan titik tertentu, yaitu secara global. Terkadang fungsi regresi polinomial lain berguna, memberikan perkiraan lokal berdasarkan segmen polinomial derajat kedua: loess(VX, VY, rentang ) mengembalikan vektor VS , digunakan oleh fungsi tersebut interp(VS, VX, VY, x) , memberikan perkiraan data terbaik (dengan koordinat titik dalam vektor VX dan VY ) segmen polinomial derajat kedua. Argumen menjangkau > 0 menunjukkan ukuran wilayah data lokal yang akan diperkirakan (nilai awal yang disarankan 0,75). Lebih menjangkau , semakin kuat efek pemulusan data. Pada umumnya menjangkau fungsi ini hampir tercapai kemunduran(VX, VY, 2) .

Contoh di bawah ini menunjukkan perkiraan suatu fungsi kompleks dengan sebaran acak ordinatnya menggunakan himpunan segmen polinomial derajat kedua (fungsi loess ) untuk dua nilai parameter menjangkau.

Dari contoh gambar dapat diketahui bahwa dengan nilai yang kecil menjangkau = 0,05 fluktuasi acak karakteristik nilai fungsi dilacak, sedangkan sudah di menjangkau = 0,5 kurva regresi menjadi hampir mulus. Sayangnya, karena kurangnya deskripsi sederhana tentang fungsi aproksimasi dalam bentuk segmen polinomial, jenis regresi ini jarang digunakan.

Melakukan regresi multivariat

MatematikaCAD Ini juga memungkinkan Anda melakukan regresi multivariat. Kasus yang paling umum adalah perkiraan permukaan dalam ruang tiga dimensi. Mereka dapat dicirikan oleh serangkaian nilai ketinggian z , sesuai dengan array dua dimensi Mxy koordinat titik (x, y) pada bidang horizontal.

Tidak ada fungsi baru yang ditentukan untuk ini. Fungsi yang telah dijelaskan digunakan dalam bentuk yang sedikit berbeda:

kemunduran(Mxy, Vz, n) mengembalikan vektor yang diminta oleh fungsi interp (VS, Mhu, Vz, V) untuk menghitung polinomial N Derajat -th, yang paling mendekati titik-titik himpunan Mxy dan Vz . Matriks Mxy m 2 yang memuat koordinat x dan y. Vzm mengandung vektor -dimensi z - koordinat yang sesuai dengan titik-titik yang ditunjukkan dalam Mx;

Loes(Mxy, Vz, span) mirip dengan loes(VX, VY, span), namun dalam kasus multidimensi;

interp(VS, Mxy, Vz, V) mengembalikan nilai z menurut vektor yang diberikan VS (dibuat oleh fungsi kemunduran atau loess) dan Mhu, Vz dan V (koordinat vektor X dan pada titik tertentu yang ada z).

Contoh interpolasi multidimensi diberikan di atas. Secara umum, regresi multivariat relatif jarang digunakan karena rumitnya pengumpulan data awal.

7 .3.3. Perkiraan dengan kombinasi fungsi linier

matematika memberi pengguna fitur bawaan linfit untuk memperkirakan data menggunakan metode kuadrat terkecil dengan kombinasi linier fungsi arbitrer.

Fungsi linfit(x , y , F ) memiliki tiga argumen:

• vektor xx koordinat titik-titik tertentu,
• vektor y y koordinat titik-titik tertentu,
• fungsi F berisi sekumpulan fungsi yang akan digunakan untuk membuat kombinasi linier.

Kami mengatur fungsi F (fungsi perkiraan dicari dalam bentuk:

Kami mendefinisikan fungsi perkiraan:

Kami menghitung variansnya:

Beras. 13 . Perkiraan dengan kombinasi fungsi linier

8.3.4.

Sekarang mari kita buat fungsi aproksimasi secara pecahan

tipe rasional. Untuk melakukan ini, kita akan menggunakan fungsinya genfit(x , y , v,F ) .

Fungsi tersebut memiliki parameter berikut:

• x, kamu vektor yang memuat koordinat titik-titik tertentu,
• F fungsi yang menentukan fungsionalitas yang diperlukan N ketergantungan parametrik dan turunan parsial dari ketergantungan ini terhadap parameter.
• ay vektor yang menentukan perkiraan awal untuk parameter pencarian.

Karena elemen nol dari fungsi tersebut F berisi fungsi yang diperlukan, kami mendefinisikan fungsinya sebagai berikut:

Hitung deviasi standarnya

Beras. 14 . Perkiraan dengan fungsi tipe arbitrer

berdasarkan genfit.

fungsi genfit tidak tersedia di semua implementasi matematika "a. Namun, masalah ini dapat diselesaikan dengan linearisasi.

Hubungan fungsional tertentu dapat dilinierkan

pengenalan variabel dan. Kemudian.

Mari kita definisikan matriks koefisien sistem normal.

Koefisien fungsi dicari dengan menyelesaikan sistem menggunakan metode matriks,

Tentukan fungsinya:

Mari kita hitung deviasi standarnya

Catatan!Kami mendapat peluang berbeda! Masalah mencari nilai minimum suatu fungsi nonlinier, terutama beberapa variabel, mungkin mempunyai beberapa penyelesaian.

Deviasi standarnya lebih besar dibandingkan dengan pendekatan polinomial, jadi Anda sebaiknya memilih pendekatan polinomial.

Mari kita sajikan hasil perkiraan dalam grafik

Beras. 15 . Perkiraan dengan fungsi tipe arbitrer

berdasarkan genfit.

Dalam kasus di mana ketergantungan fungsional ternyata cukup kompleks, ternyata cara paling sederhana untuk mencari koefisien adalah dengan meminimalkan fungsi “langsung”.

Misalkan, sebagai hasil pengukuran selama percobaan, diperoleh penetapan tabel dari fungsi tertentu f(x), menyatakan hubungan antara dua parameter geografis:

X	x 1	x 2	…	xn
f(x)	kamu 1	di 2	…	kamu n

Tentu saja, Anda dapat menemukan rumus yang menyatakan ketergantungan ini secara analitis dengan menggunakan metode interpolasi. Namun, kebetulan nilai spesifikasi analitis yang diperoleh dari fungsi pada node interpolasi dengan data empiris yang tersedia seringkali tidak berarti kebetulan perilaku fungsi asli dan fungsi interpolasi pada seluruh interval observasi. Selain itu, ketergantungan tabel indikator geografis selalu diperoleh sebagai hasil pengukuran dengan berbagai instrumen yang mempunyai kesalahan pengukuran tertentu dan tidak selalu cukup kecil. Persyaratan untuk kebetulan yang tepat dari nilai-nilai fungsi aproksimasi dan aproksimasi pada node semakin tidak dapat dibenarkan jika nilai-nilai fungsi tersebut f(x), yang diperoleh sebagai hasil pengukuran itu sendiri merupakan perkiraan.

Masalah dalam memperkirakan suatu fungsi suatu variabel sejak awal harus memperhitungkan perilaku fungsi aslinya selama seluruh interval pengamatan. Rumusan masalahnya adalah sebagai berikut. Fungsi kamu= f(x) diberikan oleh tabel (1). Penting untuk menemukan fungsi dari tipe tertentu:

yang ada di titik-titik x 1 , x 2 , …, xn mengambil nilai sedekat mungkin dengan nilai tabel kamu 1, kamu 2, …, kamu n.

Dalam praktiknya, jenis fungsi perkiraan paling sering ditentukan dengan membandingkan bentuk grafik perkiraan fungsi tersebut kamu= f(x) dengan grafik fungsi yang diketahui peneliti, ditentukan secara analitis (paling sering fungsi dasar yang tampilannya sederhana). Yakni, menurut tabel (1) dibuat plot sebar f(x), kemudian digambar kurva mulus yang mencerminkan sebaik mungkin sifat letak titik-titik tersebut. Berdasarkan kurva yang diperoleh dengan cara ini, bentuk fungsi aproksimasi ditetapkan pada tingkat kualitatif.

Perhatikan Gambar 6.

Gambar 6 menunjukkan tiga situasi:

• Pada grafik (a) hubungannya X Dan pada dekat dengan linier; garis lurus di sini dekat dengan titik pengamatan, dan titik pengamatan menyimpang darinya hanya karena pengaruh acak yang relatif kecil.
• Grafik (b) menunjukkan hubungan nyata antar besaran X Dan pada dijelaskan oleh fungsi nonlinier, dan tidak peduli garis lurus apa yang kita tarik, deviasi titik pengamatan darinya akan signifikan dan non-acak. Pada saat yang sama, cabang parabola yang digambar cukup mencerminkan sifat hubungan antar besaran.
• Pada grafik (c) terlihat hubungan yang jelas antar variabel X Dan pada absen; apapun rumus koneksi yang kita pilih, hasil parameterisasinya tidak akan berhasil. Secara khusus, kedua garis lurus yang dipilih sama-sama buruk dalam menarik kesimpulan tentang nilai yang diharapkan dari variabel pada dengan nilai variabel X.

Perlu dicatat bahwa ketergantungan fungsional yang ketat untuk tabel data awal jarang diamati, karena setiap besaran yang terlibat di dalamnya dapat bergantung pada banyak faktor acak. Namun rumus (2) (disebut rumus empiris atau persamaan regresi pada pada X) menarik karena memungkinkan Anda menemukan nilai suatu fungsi F untuk nilai non-tabel X, “menghaluskan” hasil pengukuran besaran pada, yaitu. di seluruh rentang perubahan X. Pembenaran pendekatan ini pada akhirnya ditentukan oleh kegunaan praktis dari formula yang dihasilkan.

Melalui “awan” titik-titik yang ada, Anda selalu dapat mencoba menggambar garis dari tipe yang sudah ada, yang dalam arti tertentu merupakan yang terbaik di antara semua garis dari tipe tertentu, yaitu, “paling dekat” dengan titik-titik pengamatan di dalamnya. keseluruhan. Untuk melakukan ini, pertama-tama kita mendefinisikan konsep kedekatan suatu garis dengan sekumpulan titik tertentu pada bidang. Ukuran kedekatan tersebut mungkin berbeda-beda. Namun, setiap ukuran yang masuk akal jelas harus dikaitkan dengan jarak dari titik pengamatan ke garis yang dimaksud (diberikan oleh persamaan kamu=F(x)).

Mari kita asumsikan bahwa fungsi aproksimasi F(x) di poin x 1, x 2, ..., xn urusan kamu 1 , kamu 2 , ..., kamu N. Seringkali, jumlah minimum selisih kuadrat antara pengamatan terhadap variabel terikat digunakan sebagai kriteria kedekatan kamu aku dan nilai teoritis dihitung menggunakan persamaan regresi kamu Saya. Di sini diyakini bahwa kamu aku Dan x saya- data pengamatan yang diketahui, dan F- persamaan garis regresi dengan parameter yang tidak diketahui (rumus perhitungannya akan diberikan di bawah). Suatu metode untuk memperkirakan parameter suatu fungsi aproksimasi yang meminimalkan jumlah simpangan kuadrat pengamatan variabel terikat dari nilai fungsi yang diinginkan disebut metode paling sedikit kotak (LS) atau Metode Kuadrat Terkecil (LS).

Jadi, masalah perkiraan fungsi F sekarang dapat dirumuskan sebagai berikut: untuk fungsinya F, diberikan oleh tabel (1), temukan fungsinya F tipe tertentu sehingga jumlah kuadrat Ф adalah yang terkecil.

Mari kita perhatikan metode mencari fungsi aproksimasi dalam bentuk umum menggunakan contoh fungsi aproksimasi dengan tiga parameter:

(3)

Membiarkan F(xi , a, b, c) = yi , i=1, 2, ..., n. Jumlah selisih kuadrat dari nilai-nilai yang bersesuaian F Dan F akan terlihat seperti:

Jumlah ini merupakan fungsi dari Ф (a,b,c) tiga variabel (parameter a, b Dan C). Tugasnya adalah menemukan nilai minimumnya. Kami menggunakan kondisi yang diperlukan untuk ekstrem:

Kami memperoleh sistem untuk menentukan parameter yang tidak diketahui a, b, c.

(5)

Setelah menyelesaikan sistem tiga persamaan ini dengan tiga parameter yang tidak diketahui a,b,c, kita akan mendapatkan bentuk spesifik dari fungsi yang diinginkan F(x, a, b, c). Seperti terlihat dari contoh yang diberikan, perubahan jumlah parameter tidak akan menyebabkan distorsi terhadap esensi pendekatan itu sendiri, tetapi hanya akan dinyatakan dalam perubahan jumlah persamaan dalam sistem (5).

Wajar untuk mengharapkan nilai dari fungsi yang ditemukan F(x, a, b, c) di poin x 1, x 2, ..., xn, akan berbeda dari nilai tabel kamu 1 , kamu 2 , ..., kamu n. Nilai perbedaan kamu saya -F(x saya ,a, b, c)=e saya (i=1, 2, ..., n) disebut penyimpangan nilai terukur kamu dari yang dihitung dengan rumus (3). Oleh karena itu, rumus empiris yang ditemukan (2) sesuai dengan tabel asli (1) dapat ditemukan

jumlah simpangan kuadrat, yang menurut metode kuadrat terkecil, untuk jenis fungsi perkiraan tertentu (dan nilai parameter yang ditemukan) harus yang terkecil. Dari dua perkiraan berbeda untuk fungsi tabel yang sama, dengan mengikuti metode kuadrat terkecil, yang terbaik adalah yang jumlah (4) memiliki nilai terkecil.

Dalam praktik eksperimental, sebagai fungsi perkiraan yang bergantung pada sifat plot sebar F Pendekatan fungsi dengan dua parameter sering digunakan:

Jelasnya, ketika jenis fungsi perkiraan ditetapkan, tugasnya direduksi hanya menjadi menemukan nilai parameter.

Mari kita perhatikan ketergantungan empiris yang paling umum dalam penelitian praktis.

3.3.1. Fungsi linier (regresi linier). Titik awal analisis ketergantungan biasanya memperkirakan ketergantungan linear variabel. Namun perlu diingat bahwa garis lurus “terbaik” yang menggunakan metode kuadrat terkecil selalu ada, namun garis terbaik pun tidak selalu cukup baik. Jika pada kenyataannya kecanduan kamu=f(x) bersifat kuadrat, maka tidak ada fungsi linier yang dapat mendeskripsikannya secara memadai, meskipun di antara semua fungsi tersebut pasti ada yang “terbaik”. Jika nilainya X Dan pada tidak berhubungan sama sekali, kita juga selalu dapat menemukan fungsi linier "terbaik". y=kapak+b untuk serangkaian pengamatan tertentu, tetapi dalam hal ini nilai spesifik A Dan B ditentukan hanya oleh deviasi acak dari variabel-variabel tersebut dan akan sangat bervariasi untuk sampel yang berbeda dari populasi yang sama.

Sekarang mari kita pertimbangkan masalah estimasi koefisien regresi linier secara lebih formal. Mari kita asumsikan bahwa hubungan antara X Dan kamu linier dan kita akan mencari fungsi aproksimasi yang diinginkan dalam bentuk:

Mari kita cari turunan parsial terhadap parameternya:

Mari kita substitusikan relasi yang diperoleh ke dalam sistem berbentuk (5):

atau, membagi setiap persamaan dengan n:

Mari kita perkenalkan notasi berikut:

(7)

Maka sistem terakhir akan terlihat seperti:

(8)

Koefisien sistem ini M x , Saya y , M xy , M x 2- bilangan yang dalam setiap soal aproksimasi tertentu dapat dengan mudah dihitung dengan menggunakan rumus (7), dimana x saya, kamu saya- nilai dari tabel (1). Setelah menyelesaikan sistem (8), kami memperoleh nilai parameter A Dan B, dan oleh karena itu bentuk spesifik dari fungsi linier (6).

Syarat yang diperlukan untuk memilih fungsi linier sebagai rumus empiris yang diinginkan adalah relasi:

3.3.2. Fungsi kuadrat (regresi kuadrat). Kita akan mencari fungsi aproksimasi dalam bentuk trinomial kuadrat:

Menemukan turunan parsial:

Mari kita buat sistem seperti (5):

Setelah transformasi sederhana, kita memperoleh sistem tiga persamaan linier dengan tiga persamaan yang tidak diketahui a, b, c. Koefisien sistem, seperti dalam kasus fungsi linier, hanya dinyatakan melalui data yang diketahui dari tabel (1):

(10)

Di sini kita menggunakan notasi (7), serta

Solusi sistem (10) memberikan nilai parameter a, b Dan Dengan untuk fungsi perkiraan (9).

Regresi kuadrat diterapkan jika semua ekspresi berbentuk kamu 2 -2kamu 1 + kamu 0 , kamu 3 -2 kamu 2 + kamu 1 , kamu 4 -2 kamu 3 + kamu 2 dll. sedikit berbeda satu sama lain.

3.3.3. Fungsi pangkat (regresi geometris) Sekarang mari kita cari fungsi aproksimasinya dalam bentuk:

(11)

Dengan asumsi bahwa pada tabel asli (1) nilai argumen dan nilai fungsi adalah positif, kita ambil logaritma persamaan (11) dengan syarat sebuah>0:

Sejak fungsinya F adalah perkiraan untuk fungsi tersebut F, fungsi lnF akan menjadi perkiraan untuk fungsi tersebut lnf. Mari kita perkenalkan variabel baru kamu=lnx; kemudian, sebagai berikut dari (12), lnF akan menjadi fungsi dari kamu: (kamu).

Mari kita tunjukkan

Sekarang persamaan (12) berbentuk:

itu. masalahnya direduksi menjadi menemukan fungsi aproksimasi dalam bentuk fungsi linier. Dalam praktiknya, untuk mencari fungsi aproksimasi yang diinginkan dalam bentuk fungsi pangkat (berdasarkan asumsi di atas), perlu dilakukan hal berikut:

1. menggunakan tabel ini (1) buat tabel baru, ambil nilai logaritma X Dan kamu di tabel sumber;

2. gunakan tabel baru untuk mencari parameter A Dan DI DALAM fungsi perkiraan bentuk (14);

3. Dengan menggunakan notasi (13), carilah nilai parameternya A Dan M dan substitusikan ke dalam ekspresi (11).

Kondisi yang diperlukan untuk memilih fungsi pangkat sebagai rumus empiris yang diinginkan adalah relasi:

3.3.4. Fungsi eksponensial . Misalkan tabel awal (1) sedemikian rupa sehingga disarankan untuk mencari fungsi aproksimasi dalam bentuk fungsi eksponensial:

Mari kita ambil logaritma persamaan (15):

(16)

Dengan mengambil notasi (13), kita menulis ulang (16) menjadi:

(17)

Jadi, untuk mencari fungsi aproksimasi dalam bentuk (15), perlu untuk mencatat logaritma nilai fungsi pada tabel asli (1) dan, dengan mempertimbangkannya bersama dengan nilai asli argumen, buatlah fungsi aproksimasi. dari formulir (17) untuk tabel baru. Setelah itu, sesuai dengan notasi (13), tinggal memperoleh nilai parameter yang dicari A Dan B dan substitusikan ke dalam rumus (15).

Syarat yang diperlukan untuk memilih fungsi eksponensial sebagai rumus empiris yang diinginkan adalah hubungan:

.

3.3.5. Fungsi linier pecahan. Kita akan mencari fungsi aproksimasi dalam bentuk:

(18)

Kami menulis ulang persamaan (18) sebagai berikut:

Dari persamaan terakhir berikut ini untuk mencari nilai parameter A Dan B untuk tabel tertentu (1), Anda perlu membuat tabel baru, di mana nilai argumen dibiarkan sama, dan nilai fungsi diganti dengan bilangan terbalik, dan kemudian untuk tabel yang dihasilkan, temukan perkiraan fungsi formulir kapak+b. Nilai parameter ditemukan A Dan B substitusikan ke rumus (18).

Syarat yang diperlukan untuk memilih fungsi linier pecahan sebagai rumus empiris yang diinginkan adalah relasi:

.

3.3.6. Fungsi logaritma. Biarkan fungsi perkiraannya berbentuk:

Sangat mudah untuk melihat bahwa untuk menuju fungsi linier cukup dengan melakukan substitusi lnx=kamu. Berikut ini untuk menemukan nilainya A Dan B Anda perlu membuat logaritma nilai argumen pada tabel asli (1) dan, dengan mempertimbangkan nilai yang diperoleh bersama dengan nilai asli fungsi, temukan fungsi perkiraan dalam bentuk fungsi linier untuk tabel baru yang diperoleh. Kemungkinan A Dan B substitusikan fungsi yang ditemukan ke dalam rumus (19).

Kondisi yang diperlukan untuk memilih fungsi logaritma sebagai rumus empiris yang diinginkan adalah relasi:

.

3.3.7. Hiperbola. Jika plot sebar yang dibuat dari tabel (1) memberikan cabang hiperbola, fungsi aproksimasinya dapat dicari dalam bentuk.