Теория об изменении кинетической энергии механической системы. Теорема об изменении кинетической энергии. Пример решения задачи. Закон об изменении механической энергии

механической системы

Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех ее материальных точек

Вычисление кинетической энергии твердого тела

1. Поступательное движение

Как известно, при поступательном движении скорости всех точек тела в один и тот же момент времени равны, тогда (83) можно представить в виде

. (84)

При поступательном движении тела, его кинетическая энергия равна половине произведения массы на квадрат скорости центра масс.

2. Вращательное движение твердого тела

При вращательном движении скорость каждой точки тела

. (85)

Подставим (85) в (83):

.

Принимая во внимание (59), получим

. (86)

При вращательном движении кинетическая энергия равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.

3 . Плоское движение

Плоское движение можно представить как вращение относительно полюса (например, центра масс) и движения вместе с полюсом, тогда

. (87)

Кинетическая энергия тела при плоском движении равна сумме кинетических энергий от поступательного движения вместе с центром масс и вращательного движения относительно центра масс.

Теорема: Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ всех внутренних и внешних сил системы на том же перемещении

. (88)

Замечания :

1. Введенная величина кинетической энергии системы в отличие от количества движения системы и кинетического момента является скалярной величиной. При этом:

Q =0 при вращательном движении и покое;

K O =0 при поступательном движении или покое;

T

Таким образом, в отличие от теоремы об изменении количества движения и кинетического момента, данная теорема пригодна для изучения любого вида движения, так как T =0 только для неподвижной системы.

2. В отличие от упомянутых теорем данная теорема учитывает действие внутренних сил системы.

Некоторые случаи вычисления работы

1. Работа момента силы M Z относительно оси равна произведению момента на угол поворота  тела относительно оси

. (89)

2. Сумма работ внутренних сил абсолютно твердого тела (недеформируемого) всегда равна нулю.

3. Работа момента трения качения
.

,

где  - коэффициент трения качения;

R – радиус цилиндра;

s – длина дуги, равная отрезку пути, пройденного центром масс C вдоль поверхности;


- угол поворота осей цилиндра в процессе движения;

N – нормальная реакция поверхности;

P – сила тяжести;

F тр – сила трения скольжения.

Дифференциальные уравнения поступательного, вращательного и плоского движения твердого тела

1. Поступательное движение

При поступательном движении все точки тела движутся по одинаковым траекториям и в один и тот же момент времени имеют одинаковые ускорения. Тогда для описания движения можно использовать теорему о движении центра масс (67). Проектируем это уравнение на координатные оси

Система (90) представляет собой дифференциальные уравнения поступательного движения твердого тела.

2. Вращательное движение

Пусть твердое тело совершает вращение относительно оси под действием сил. Динамической характеристикой вращательного движения твердого тела является кинетический моментK z , а характеристикой вращательного действия силы  момент силы относительно оси. Поэтому для описания вращательного движения твердого тела относительно неподвижной оси воспользуемся теоремой об изменении кинетического момента (81)

. (91)

При вращательном движении
, тогда

,

учитывая, что I z =const, в итоге получим

. (92)

Уравнение (92) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

Найденный угол  будет определять положение тела, совершающего вращательное движение, в любой момент времени.

3. Плоское движение

Положение тела, совершающего плоское движение, в любой момент времени определяется положением полюса и углом поворота тела относительно полюса. Если за полюс принять центр масс тела, то уравнение его движения можно найти по теореме о движении центра масс (67), а вращательное движение относительно центра будет определяться уравнением (92), справедливым и для движения системы относительно оси, проходящей через центр масс. Тогда дифференциальные уравнения плоского движения твердого тела имеют вид

Интегральная (конечная) форма . Теорема об изменении кинетической энергии материальной точки: изменение кинетической энергии мате-риальной точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении .

Теорема об изменении кинетической энергии механической системы формулируется: изменение кинетической энергии меха-нической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении:

В случае неизменяемой системы сумма работ внутренних сил на любом перемещении равна нулю (), тогда

Закон сохранения механической энергии. При движении механической системы под действием сил, имеющих потенциал, изменения кинетической энергии системы определяются зависимостями:

Откуда ,

Сумму кинетической и потенциальной энергий системы называют полной механической энергией системы.

Таким образом , при движении механической системы в стационар-ном потенциальном поле полная механическая энергия системы при движении остается неизменной .

Задача. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным s (рис. 3.70).

В задаче принять:

Решение. На механическую систему действуют активные силы , , . Применяя принцип освобождения от связей системы, покажем реакции шарнирно-неподвижной опоры 2 и шероховатой наклонной поверхности. Направления скоростей тел системы изобразим с учетом того, что тело 1 спускается.

Задачу решим, применяя теорему об изменении кинетической энергии механической системы :

где Т и - кинетическая энергия системы в начальном и конечном положениях; - алгебраическая сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; - сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями:

Так как в начальном положении система покоилась, то . Следовательно:

Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2, 3:

Кинетическая энергия груза 1, движущегося поступательно, равна:

Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz , перпендикулярной плоскости чертежа:

Кинетическая энергия тела 3 в его поступательном движении:

Таким образом,

Выражение кинетической энергии содержит неизвестные скорости всех тел системы. Начать определение необходимо с . Избавимся от лишних неизвестных, составив уравнения связей.

Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.

Скорость любой точки обода малого радиуса равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r:

Отсюда выразим угловую скорость тела 2:

Вращательная скорость любой точки обода блока большого радиуса , с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой - скорости тела 3:

Подставив значение угловой скорости, получим:

Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:

Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):

Момент инерции тела 2 равен:

Подставляя значения масс тел и момента инерции тела 2, запишем:

Определение суммы работ всех внешних сил системы на заданном перемещении.

Теперь согласно теореме об изменении кинетической энергии механической системы приравняем значения Т и

Скорость тела 1 получим из выражения (г)

Ускорение тела 1 можно определить, продифференцировав по времени равенство (г).

Просмотр: эта статья прочитана 49915 раз

Pdf Выберите язык... Русский Украинский Английский

Краткий обзор

Полностью материал скачивается выше, предварительно выбрав язык

Два случая преобразования механического движения материальной точки или системы точек:

1. механическое движение переносится с одной механической системы на другую в качестве механического движения;
2. механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоту, электричество и т.д.).

Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки или механической системы. Мерой действия силы в этом случае является вектор импульса силы.

Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы

Кинетическая энергия

Кинетическая энергия это способность тела преодолевать препятствование во время движения.

Кинетическая энергия материальной точки

Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.

Кинетическая энергия:

• характеризует и поступательное, и вращательное движения;
• не зависит от направления движения точек системы и не характеризует изменение этих направлений;
• характеризует действие и внутренних, и внешних сил.

Кинетическая энергия механической системы

Кинетическая энергия системы равняется сумме кинетических энергий тел системы. Кинетическая энергия зависит от вида движения тел системы.

Определение кинетической энергии твердого тела при разных видах движения движениях.

Кинетическая энергия поступательного движения
При поступательном движении кинетическая энергия тела равна Т =m V 2 /2.

Мерой инертности тела при поступательном движении является масса.

Кинетическая энергия вращательного движения тела

При вращательном движении тела кинетическая энергия равняется половине произведения момента инерции тела относительно оси вращения и квадрата его угловой скорости.

Мерой инертности тела при вращательном движении является момент инерции.

Кинетическая энергия тела не зависит от направления вращения тела.

Кинетическая энергия плоскопаралельного движения тела

При плоскопаралельном движении тела кинетическая энергия равна

Работа силы

Работа силы характеризует действие силы на тело при некотором перемещении и определяет изменение модуля скорости подвижной точки.

Элементарная работа силы

Элементарная работа силы определяется как скалярная величина, равная произведению проекции силы на касательную к траектории, направленную в направлении движения точки, и бесконечно малого перемещения точки, направленного вдоль этой касательной.

Работа силы на конечном перемещении

Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.

Работа силы на конечном перемещении М 1 М 0 равняется интегралу вдоль этого перемещения от элементарной работы.

Работа силы на перемещении М 1 М 2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М 1 и М 0 .

Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).

Теоремы о работе силы

Теорема 1 . Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Теорема 2. Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.

Мощность

Мощность - это величина, которая определяет работу силы за единицу времени.

Единицей измерения мощности есть 1Вт = 1 Дж/с.

Случаи определения работы сил

Работа внутренних сил

Сумма работ внутренних сил твердого тела на любом его перемещении равна нулю.

Работа силы тяжести

Работа силы упругости

Работа силы трения

Работа сил, приложенных к вращающемуся телу

Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота.

Сопротивление качению

В зоне контакта неподвижого цилиндра и плоскости возникает местная деформация контактного сжатия, напряжение распределяются по эллиптическому закону и линия действия равнодействующей N этих напряжений совпадает с линией действия силы нагрузки на цилиндр Q. При перекатывании цилиндра распределение нагрузки становится несимметричным с максимумом, смещенным в сторону движения. Равнодействующая N смещается на величину k - плечо силы трения качения, которая еще назвается коэффициентом трения качения и имеет размерность длины (см)

Теорема об изменении кинетической энергии материальной точки

Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на том же перемещении.

Теорема об изменении кинетической энергии механической системы

Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.

Теорема об изменении кинетической энергии твердого тела

Изменение кинетической энергии твердого тела (неизменной системы) на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.

КПД

Силы, действующие в механизмах

Силы и пары сил (моменты), которые приложены к механизму или машине, можно разделить на группы:

1.Движущие силы и моменты, совершающие положительную работу (приложенные к ведущим звеньям, например, давление газа на поршень в ДВС).

2. Силы и моменты сопротивления, совершающие отрицательную работу:

• полезного сопротивления (совершают требуемую от машины работу и приложены к ведомым звеньям, например сопротивление поднимаемого машиной груза),
• силы сопротивления (например, силы трения, сопротивление воздуха и т.п.).

3. Силы тяжести и силы упругости пружин (как положительная, так и отрицательная работа, при этом работа за полный цикл равна нулю).

4. Силы и моменты, приложенные к корпусу или стойке извне (реакция фундамента и т.п.), которые не совершают работу.

5. Силы взаимодействия между звеньями, действующие в кинематических парах.

6. Силы инерции звеньев, обусловленные массой и движением звеньев с ускорением, могут осуществлять положительную, отрицательную работу и не совершать работы.

Работа сил в механизмах

При установившемся режиме работы машины ее кинетическая энергия не изменяется и сумма работ приложенных к ней движущих сил и сил сопротивления равна нулю.

Работа, затрачиваемая на приведение машины в движение, расходуется на преодоление полезных и вредных сопротивлений.

КПД механизмов

Механический коэффициент полезного действия при установившемся движении равен отношению полезной работы машины к работе, затраченной на приведение машины в движение:

Элементы машины могут соединяться последовательно, параллельно и смешанно.

КПД при последовательном соединении

При последовательном соединении механизмов общий КПД меньше с наименьшего КПД отдельного механизма.

КПД при параллельном соединении

При параллельном соединении механизмов общий КПД больше наименьшего и меньше наибольшего КПД отдельного механизма.

Формат: pdf

Язык: русский, украинский

Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.

Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.

Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается

Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается

Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия

Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .

Отсюда для работы получаем

\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .

Кинетическая энергия обозначается буквой E k .

\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)

Тогда равенство (1) можно записать в таком виде:

\(~A = E_{k2} - E_{k1}\) . (3)

Теорема о кинетической энергии

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:

\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)

Физический смысл кинетической энергии

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей

Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)

где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .

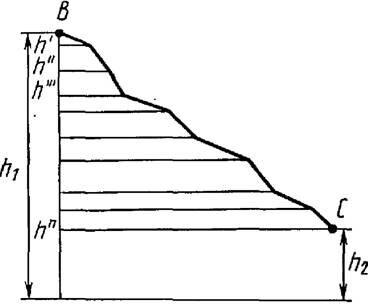
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

\(~A = - (E_{p2} - E_{p1})\) . (9)

Потенциальная энергия обозначается буквой Е p .

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

\(~E_p = m \cdot g \cdot h\) . (10)

Физический смысл потенциальной энергии взаимодействия тела с Землей

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:

\(~E_p = -m \cdot g \cdot h\) .

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна

\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.

Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна

\(~E_p = m \cdot g \cdot h\) ,

где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:

\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)

где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда

\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

\(~E_p = \frac{k \cdot x^2}{2}\) . (15)

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (16)

Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),

\(~E_p = A\) .

Физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.

Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (17)

По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:

\(~A = E_{k2} - E_{k1}\) . (18)

Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)

Закон сохранения энергии в механических процессах :

сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией .

Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.

В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.

Закон сохранения энергии раскрывает физический смысл понятия работы :

работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон об изменении механической энергии

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:

\(~A_{vn} = \Delta E = E - E_0\) . (20)

где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.

Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна

\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,

где s 12 – путь тела между точками 1 и 2.

Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.

Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

Закон сохранения и превращения энергии

при любых физических взаимодействиях энергия превращается из одной формы в другую.

Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:

\(~A_{tr} = F_{tr} \cdot s_{12}\) ,

Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:

Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература

1. Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
2. Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
3. Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
4. Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.

Если рассмотреть какую-нибудь точку системы с мас­сой , имеющую скорость , то для этой точки будет

,

где и - элементарные работы действующих на точку внеш­них и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим

,

. (2)

Равенство выражает теорему об изменении кине­тической энергии системы в дифференциальной форме.

Если полученное выражение отнести к элементарному промежутку времени, в течение которого произошло рассматриваемое перемещение, можно получить вторую формулировку для дифференциальной формы теоремы: производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних () и внутренних () сил, т.е.

Дифференциальными формами теоремы об изменении кинетической энергии можно воспользоваться для составления дифференциальных уравнений движения, но это делается достаточно редко, потому что есть более удобные приемы.

Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна , в положение, где значение кинетической энергии становится равным , будемиметь

Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом пере­мещении всех приложенных к системе внешних и внутренних сил.

В отличие от предыдущих теорем, внутренние силы в уравнениях не исключаются. В самом деле, если и - силы взаимодействия между точками и системы (см. рис.51), то . Но при этом точка , может перемещаться по направ­лению к , а точка - по направлению к . Работа каждой из сил бу­дет тогда положительной и сумма работ нулем не будет. Примером мо­жет служить явление отката. Внутренние силы (силы давления), действующие и на снаряд и на откатывающиеся части, совершают здесь положительную работу. Сумма этих работ, не равная нулю, и изменяет кинетическую энергию системы от вели­чины в начале выстрела до величины конце.

Другой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, не упругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.

Рассмотрим два важных частных случая.

1) Неизменяемая система . Неизменяемой будем называть систему, в которой расстояния между точками приложения внутрен­них сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

Рис.51

Пусть две точки и неизменяе­мой системы (pис.51), действующие друг на друга с силами и () имеют в данный момент скорости и . Тогда за промежу­ток времени dt эти точки совершат элементарные перемещения и , направленные вдоль векторов и . Но таккак отрезок является неизменяемым, то по известной теореме кинематики про­екции векторов и , а, следовательно, и перемещений и на направление отрезка будут равны друг другу, т.е. . Тогда элементарные работы сил и будут одинаковы по мо­дулю и противоположны по знаку и в сумме дадут нуль. Этот резуль­тат справедлив для всех внутренних сил при любом перемещении системы.

Отсюда заключаем, что для неизменяемой системы сумма работ всех внутренних сил равна нулю и уравнения принимают вид

2) Система с идеальными связями . Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда

,

где - элементарная работа действующих на k- ю точку системы внешних и внутренних активных сил, a - элементарная работа реакций наложенных на ту же точку внешних и внутренних связей.

Как видим, изменение кинетической энергии системы зависит от работы и активных сил и реакций связей. Однако можно ввести по­нятие о таких «идеальных» механических системах, у которых нали­чие связей не влияет на изменение кинетической энергии системы при ее движении. Для таких связей должно, очевидно, выполняться условие:

Если для связей, не изменяющихся со временем, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи назы­вают идеальными. Для механической системы, на которую наложены только не изменяющиеся со временем идеальные связи, будем, очевидно, иметь

Таким образом, изменение кинетической энергии системы с идеальными, не изменяющимися со временем связями при любом ее перемещении равно сумме работ на этом перемещении, приложенных к системе внешних и внутренних активных сил.

Механическая система называется консервативной (энергия ее как бы законсервирована, не изменяется), если для нее имеет место интеграл энергии

или (3)

Это есть закон сохранения механической энергии: при движении системы в потенциальном поле механическая энергия ее (сумма потенциальной и кинетической) все время остается неизменной, постоянной.

Механическая система будет консервативной, если действующие на нее силы потенциальны, например сила тяжести, силы упругости. В консервативных механических системах с помощью интеграла энергии можно проводить проверку правильности составления дифференциальных уравнений движения. Если система консервативна, а условие (3) не выполняется, значит при составлении уравнений движения допущена ошибка.

Интегралом энергии можно воспользоваться для проверки правильности составления уравнений и другим способом, без вычисления производной. Для этого следует после проведения численного интегрирования уравнений движения вычислить значение полной механической энергии для двух различных моментов времени, например, начального и конечного. Если разница значений окажется сопоставимой с погрешностями вычислений, это будет свидетельствовать о правильности используемых уравнений.

Все предыдущие теоремы позволяли исключить из уравнений движения внутренние силы, но все внешние силы, в том числе и наперед неизвестные реакции внешних связей, в уравнениях сохранялись. Практическая ценность теоремы об изменении кинетической энергии состоит в том, что при не изменяющихся со временем идеальных связях она позволит исключить из уравнений движения все наперед неизвестные реакции связей.