Свободные колебания. Основное свойство колебательных систем Возвращающая сила в различных колебательных системах

«Колебания физика» - Найдем разность фаз?? между фазами смещения х и скорости?x. Силы же имеющие иную природу, но удовлетворяющие (1) называются квазиупругими. Т.к. синус и косинус изменяются в пределах от +1 до – 1, Фаза измеряется в радианах. , Или. 1.5 Энергия гармонических колебаний. Разделы оптики: геометрическая, волновая, физиологическая.

«Вынужденные колебания резонанс» - Резонанс моста под действием периодических толчков при прохождении поезда по стыкам рельсов. В радиотехнике. Резонанс весьма часто наблюдается в природе и играет огромную роль в технике. Характер явления Резонанс существенно зависит от свойств колебательной системы. Роль резонанса. В др. случаях резонанс играет положительную роль, например:

«Колебательное движение» - Особенность колебательного движения. Крайнее правое положение. Крайнее левое положение. Маятник часов. V=0 м/с а=max. Механизм колебания. Ветки деревьев. Примеры колебательных движений. Положение равновесия. Игла швейной машинки. Рессоры вагона. Условия возникновения колебаний. Качели. Колебательное движение.

«Урок механические колебания» - II. 1. Колебания 2. Колебательная система. 2. Колебательная система – система тел, способных совершать колебательные движения. Х [м] - смещение. 1. Муниципальное общеобразовательное учреждение – Гимназия №2. Свободные колебания. 3. Основное свойство колебательных систем. Техническая поддержка урока:

«Колебание точки» - Вынужденные колебания. 11. 10. 13. 12. Малое сопротивление. Коэффициент динамичности. 4. Примеры колебаний. 1. Примеры колебаний. Движение является затухающим и апериодичным. Движение = свободные колебания + вынужденные колебания. Лекция 3: прямолинейные колебания материальной точки. 6. Свободные колебания.

«Физический и математический маятник» - Выполнила Юнченко Татьяна. Математический маятник. Презентация

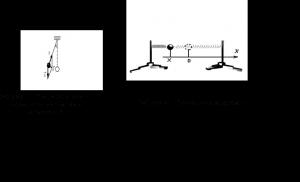
Земля, подставка и подвешенное к подставке тело (см. рис. 3) образуют колебательную систему, называемую физическим маятником. Стойки, две пружины и тело m (см. рис. 4) образуют колебательную систему, которую обычно называют горизонтальным пружинным маятником. Всем колебательным системам присущ ряд общих свойств. Рассмотрим главные из них.

1 У каждой колебательной системы есть состояние устойчивого равновесия. У физического маятника – это положение, в котором центр массы подвешенного тела находится на одной вертикали с точкой подвеса. У вертикального пружинного маятника – это положение, в котором сила тяжести уравновешивается силой упругости пружины. У горизонтального пружинного маятника – это положение, при котором обе пружины деформированы одинаково.

2 После того как колебательная система выведена из положения устойчивого равновесия, появляется сила, возвращающая систему в устойчивое положение. Происхождение этой силы может быть различным. Так, у физического маятника – это равнодействующая f силы тяжести G и силы упругости T (рис.5), а у пружинных маятников – это сила упругости пружин (рис. 6).

3 Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Перечисленные свойства приводят к тому, что если колебательную систему тем или иным способом вывести из состояния устойчивого равновесия, то в ней в отсутствие внешних сил возникнут и некоторое время будут сохраняться колебания. Возникшие колебания могли бы продолжаться неограниченно долго, если бы в колебательной системе не было трения (сопротивления). Именно такие, идеальные колебательные системы мы во многих случаях будем рассматривать. Идеальная колебательная система имеет два определяющих признака:

а) в ней отсутствует трение (сопротивление) и, следовательно, не происходит необратимых превращений энергии;

б) параметры такой колебательной системы (длина нити, масса колеблющегося тела, жесткость пружины) постоянны.

Примером идеальной колебательной системы может служить так называемый математический маятник, представляющий собой груз малых размеров, подвешенный на гибкой невесомой и нерастяжимой пружине. Длина нити и масса груза в процессе колебания маятника остаются неизменными. Если нить считать бесконечно тонкой и идеально гибкой, а размеры груза бесконечно малыми, точечными, то при колебаниях математического маятника трения не будет.

В реальных колебательных системах имеется трение, а параметры системы в процессе колебательного движения немного изменяются. Так, маятник, представляющий собой груз конечных размеров, подвешенный на шелковой нити, нельзя считать в полном смысле идеальной колебательной системой, так как в процессе его колебательного движения действует сопротивление воздуха и трение в точке подвеса, а длина нити изменяется (хотя и совсем незначительно). Но при малых колебаниях такого маятника сопротивление воздуха мало, а длина нити меняется столь незначительно, что с известным приближением можно этот маятник считать почти идеальной колебательной системой. Это относится также к пружинному маятнику. Его можно считать идеальной колебательной системой, если масса колеблющегося тела и жесткость пружины постоянны, а трение столь мало, что его можно не учитывать.

1 Свободные колебания. Колебания, происходящие в колебательной системе, не подверженной действию периодических внешних сил, называются свободными колебаниями. Для возникновения свободных колебаний на колебательную систему должно быть оказано из вне кратковременное воздействие, выводящее систему из состояния равновесия (отклонение из среднего положения маятника, зажатой в тисках стальной линейки, струны и т.п.).

2 Осциллограмма колебаний .Если грузом маятника будет служить сосуд с чернилами, в котором имеется узкое отверстие, то при колебаниях маятника.

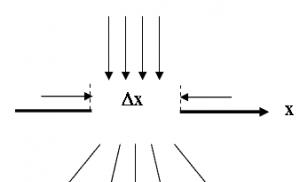
Всякое колебательное движение есгь движение, происходящее с ускорением, поэтому на колеблющиеся тела должны действовать силы, сообщающие им эти ускорения. В частности, если точечное тело массой совершает гармоническое колебание, то, согласно второму закону механики, на него должна действовать сила, равная

где Направление силы совпадает с направлением ускорения, а вектор ускорения при гармонических колебаниях, согласно формуле (4.5), всегда направлен к положению равновесия. Таким образом, для того чтобы тело совершало гармоническое колебательное движение, на него должна действовать сила, всегда направленная к положению равновесия, а по величине - прямо пропорциональная смещению от этого положения. При исследовании колебательных систем можно легко найти коэффициент пропорциональности между действующей на тело силой и смещением х этого тела от положения равновесия; тогда, зная еще и массу колеблющегося тела, можно вычислить частоту и период колебания; из соотношения следует:

Силы, всегда направленные к положению равновесия, называются возвращающими. Рассмотрим несколько примеров:

1. Колебательная система, состоящая из массы и пружины (см. рис. 1.36, б). Возвращающей силой является упругая сила, действующая на тело со стороны деформированной пружины. Эта сила при малых деформациях прямо пропорциональна изменению длины пружины Приложив к пружине внешние силы и измерив вызванные ими удлинения

(или сжатия) пружины, можно найти коэффициент упругости пружины и по формуле (4.10) рассчитать частоту колебаний тел, прикрепленных к концам пружины. При этом колебания будут гармоническими и со постоянны) только в том случае, если на колеблющееся, тело не действуют никакие другие силы, кроме возвращающей причем коэффициент от которого, согласно формуле (4.10), зависит частота колебаний, должен все время сохраняться постоянным. В частности, если температура пружины изменяется, то а следовательно, и частота колебаний также изменяются; колебания не будут гармоническими.

2. Система, совершающая крутильные (поворотные) колебания (см. рис. 1.38, б). При крутильных колебаниях на тело действует возвращающий момент, приостанавливающий отклонение тела от состояния равновесия и затем сообщающий ему обратное движение. Возвращающий момент возникает при деформации (кручении) пружины (или стержня), к которой прикреплено колеблющееся тело. При малых углах отклонения этот момент прямо пропорционален углу отклонения.

Если крутильные колебания гармонические, т. е.

то угловая скорость и угловое ускорение при повороте также изменяются по гармоническому закону:

Возвращающий момент найдем как произведение углового ускорения на момент инерции колеблющегося тела:

где постоянная величина (если момент инерции тела при колебаниях не изменяется). Этот коэффициент можно найти, приложив к пружине (или стержню) внешние скручивающие моменты и измеряя углы скручивания а:

тогда частота и период колебаний определяются по формулам:

Согласно выражению (4.13), при гармонических крутильных колебаниях возвращающий момент должен быть точно пропорционален углу отклонения; если эта пропорциональность не соблюдается (например, при очень больших углах поворота), то колебания не будут гармоническими (хотя при отсутствии трения будут незатухающими).

3. Физический маятник (рис. 1.40). Возвращающим моментом является момент силы тяжести, имеющий знак,

противоположный знаку угла отклонения а и равный

где расстояние от точки опоры до центра тяжести тела.

При малых углах отклонения (угол а - в радианах); тогда возвращающий момент

пропорционален углу отклонения и колебания маятника будут гармоническими.

Сравнивая с выражением (4.13), получим следовательно,

При больших углах отклонения, а также при деформации тела во время колебаний (переменные колебания оказываются негармоническими, хотя они при отсутствии или компенсации трения могут быть незатухающими.

4. Математический маятник представляет собой точечное тело массой подвешенное к невесомой и нерастяжимой нити длиной I (рис. 1.41). Возвращающей силой является проекция силы тяжести на направление движения тела; имеем:

В радианах). Замечаем, что условие пропорциональности между возвращающей силой и смещением от положения равновесия х здесь также не соблюдается, поэтому колебания этого маятника не являются гармоническими. Но если углы а малы, так что то

так как эта сила всегда направлена к положению равновесия и поэтому имеет знак, противоположный знаку то

В этом случае колебания можно полагать гармоническими; сравнивая с выражением (4.9), получаем:

т. е. частота и период колебаний не зависят от массы колеблющегося тела, а определяются только длиной нити и ускорением силы тяжести (колебаниями маятников пользуются для определения Для постоянства коэффициента а следовательно, и частоты колебаний со необходимо постоянство Между тем сила действующая вдоль нити, может вызвать ее удлинение, которое будет минимальным в крайних положениях и максимальным при прохождении тела через точку О. Поэтому, чтобы колебания маятника были гармоническими, необходимо кроме малости углов отклонения дополнительно еще и условие нерастяжимости нити.

Из этих примеров видно, что при малых амплитудах частота (или период) колебаний определяется только свойствами системы. Однако при больших отклонениях от положения равновесия линейная зависимость возвращающей силы от смещения а также возрастающего момента от угла поворота строго не соблюдается и частота колебаний зависит в некоторой степени также и от амплитуды колебаний или