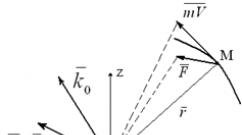
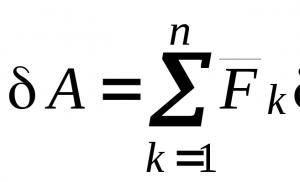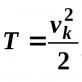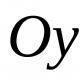Primjeri projekcije tačaka. Projektovanje tačke na tri projekcijske ravni. Jednadžba prave linije za dvodimenzionalne i trodimenzionalne prostore

Tačka, kao matematički koncept, nema dimenzije. Očigledno, ako je objekt projekcije nultodimenzionalan objekt, onda je razgovor o njegovoj projekciji besmislen.

Slika 9 Slika 10

U geometriji je pod tačkom preporučljivo uzeti fizički objekt linearnih dimenzija. Uobičajeno se kao tačka može uzeti lopta beskonačno malog radijusa. Sa takvim tumačenjem pojma tačke može se govoriti o njenim projekcijama.

Prilikom konstruisanja ortogonalnih projekcija tačke treba se rukovoditi prvim nepromenljivim svojstvom ortogonalne projekcije: ortogonalna projekcija tačke je tačka.

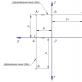
Položaj tačke u prostoru određen je sa tri koordinate: X, Y, Z, pokazujući vrijednosti udaljenosti na kojima je tačka uklonjena od ravni projekcije. Da biste odredili ove udaljenosti, dovoljno je odrediti tačke susreta ovih pravih sa ravnima projekcije i izmjeriti odgovarajuće vrijednosti, koje će ukazati na vrijednosti apscise, respektivno X, ordinate Y i primenjuje Z tačke (sl. 10).

Projekcija tačke je osnova okomice spuštene iz tačke na odgovarajuću ravan projekcije. Horizontalna projekcija bodova a naziva se pravokutna projekcija točke na horizontalnu projekcijsku ravan, frontalna projekcija a /- odnosno na frontalnoj ravni projekcija i profil a // - na profilnoj ravni projekcija.

Direktno Aa, Aa / i Aa // nazivaju se projektovane linije. Štaviše, pravo Aa, tačka projektovanja A na horizontalnoj ravni projekcija, tzv horizontalno projektovana ravna linija, Aa / i Aa //- odnosno: frontalno i profilisane ravne linije.

Dvije projektovane prave koje prolaze kroz tačku A definiraju ravan, koja se obično naziva projektovanje.

Prilikom transformacije prostornog rasporeda, prednja projekcija tačke Aa / ostaje na svom mestu, kao da pripada ravni, koja ne menja svoj položaj tokom transformacije koja se razmatra. Horizontalna projekcija - a zajedno s horizontalnom ravninom projekcije rotirati će se u smjeru kretanja u smjeru kazaljke na satu i nalazit će se u jednoj okomici na os NS sa frontalnom projekcijom. Projekcija profila - a //će se rotirati zajedno sa ravninom profila i do kraja transformacije će zauzeti poziciju prikazanu na slici 10. U ovom slučaju - a // pripadaće okomito na osu Z izvučeno iz tačke a / i biće uklonjen sa ose Z na istoj udaljenosti kao i horizontalna projekcija a uklonjen sa ose NS... Stoga se veza između horizontalne i profilne projekcije tačke može uspostaviti pomoću dva ortogonalna segmenta aa y i a y a // i luk kruga koji ih spaja sa centrom u tački presjeka osi ( O- porijeklo). Označena veza služi za pronalaženje nedostajuće projekcije (za dvije date). Položaj profilne (horizontalne) projekcije prema datim horizontalnim (profilnim) i čeonim projekcijama može se pronaći pomoću prave linije povučene pod uglom od 45 0 od ishodišta do ose Y(ova simetrala se zove prava linija k- Mongeova konstanta). Prva od ovih metoda je poželjnija kao preciznija.

dakle:

1. Tačka u prostoru je uklonjena:

iz horizontalne ravni H Z,

iz frontalne ravni V po vrijednosti date koordinate Y,

iz profilne ravni W po vrijednosti koordinate. X.

2. Dvije projekcije bilo koje tačke pripadaju istoj okomici (jedna komunikaciona linija):

horizontalno i frontalno - okomito na os X,

horizontalno i profilno - okomito na Y os,

frontalni i profilni - okomito na Z os.

3. Položaj tačke u prostoru u potpunosti je određen položajem njene dvije ortogonalne projekcije. Stoga - bilo koje dvije date ortogonalne projekcije tačke se uvijek mogu koristiti za konstruiranje njene treće projekcije koja nedostaje.

Ako tačka ima tri određene koordinate, onda se takva tačka naziva tačka opšte pozicije. Ako tačka ima jednu ili dve koordinate imaju nultu vrednost, onda se takva tačka naziva tačka određene pozicije.

Rice. 11 Fig. 12

Na slici 11 dat je prostorni crtež tačaka određene pozicije, na slici 12 - složeni crtež (dijagrami) ovih tačaka. Poenta A pripada frontalnoj ravni projekcija, tačka V- horizontalna projekcijska ravan, tačka WITH- profilna ravan projekcije i tačke D- apscisa ose ( NS).

Projekcioni aparati

Uređaj za projekciju (slika 1) uključuje tri projekcijske ravni:

π 1 - horizontalna ravan projekcija;

π 2 - ravnina frontalne projekcije;

π 3- profilna ravan projekcija .

Ravnine projekcije se nalaze međusobno okomite ( π 1^ π 2^ π 3), a njihove linije presjeka čine osi:

Presjek ravni π 1 i π 2 formiraju osu 0X (π 1∩ π 2 = 0X);

Presjek ravni π 1 i π 3 formiraju osu 0Y (π 1∩ π 3 = 0Y);

Presjek ravni π 2 i π 3 formiraju osu 0Z (π 2∩ π 3 = 0Z).

Tačka preseka osa (OH∩OY∩OZ = 0) smatra se početnom tačkom (tačka 0).

Pošto su ravni i ose međusobno okomite, ovaj aparat je sličan Dekartovom koordinatnom sistemu.

Projekcione ravni su podijeljene na osam oktanata (na sl. 1 označene su rimskim brojevima). Projekcione ravni se smatraju neprozirnim, a posmatrač je uvek unutra I-th oktant.

Ortogonalna projekcija sa projekcijskim centrima S 1, S 2 i S 3 za horizontalnu, frontalnu i profilnu projekcijsku ravninu.

A.

Iz centara projekcije S 1, S 2 i S 3 projekcijske zrake izlaze l 1, l 2 i l 3 A

- A 1 A;

- A 2- frontalna projekcija tačke A;

- A 3- projekcija profila tačke A.

Tačku u prostoru karakteriziraju njene koordinate A(x, y, z). Poeni Sjekira, A y i A z odnosno na osovinama 0X, 0Y i 0Z pokazati koordinate x, y i z bodova A... Na sl. 1 daje sve potrebne oznake i prikazuje veze između tačaka A prostor, njegove projekcije i koordinate.

Point plots

Da dobijem tačku A(sl. 2), u projekcijskom aparatu (sl. 1) ravan π 1 A 1 0X π 2... Onda avion π 3 sa projekcijom tačke A 3, rotirajte u smjeru suprotnom od kazaljke na satu oko ose 0Z, prije nego što ga poravnate s ravninom π 2... Smjer rotacije ravnina π 2 i π 3 prikazano na sl. 1 sa strelicama. Istovremeno, direktno A 1 A x i A 2 A x 0X okomito A 1 A 2 i ravno A 2 A x i A 3 A xće se nalaziti na zajedničkoj osi 0Z okomito A 2 A 3... U nastavku će se ovi redovi zvati, respektivno. vertikalno i horizontalno veze linije.

Treba napomenuti da prilikom prijelaza sa projekcijskog aparata na dijagram projektirani objekt nestaje, ali se čuvaju svi podaci o njegovom obliku, geometrijskim dimenzijama i položaju u prostoru.

A(x A, y A, z Ax A, y A i z A u sledećem nizu (slika 2). Ova sekvenca se naziva tehnika crtanja tačaka.

1. Ose se crtaju ortogonalno OX, OY i OZ.

2. Na osi OX x A bodova A i dobiti poziciju tačke Sjekira.

3. Prolazna tačka Sjekira okomito na osu OX

Sjekira u smjeru ose OY numerička vrijednost koordinate je odgođena y A bodova A A 1 na dijagramu.

Sjekira u smjeru ose OZ numerička vrijednost koordinate je odgođena z A bodova A A 2 na dijagramu.

6. Kroz tačku A 2 paralelno sa osom OX povučena je horizontalna komunikacijska linija. Presjek ove linije i ose OZće dati poziciju tačke A z.

7. Na horizontalnoj komunikacijskoj liniji od tačke A z u smjeru ose OY numerička vrijednost koordinate je odgođena y A bodova A i određuje se položaj profilne projekcije tačke A 3 na dijagramu.

Karakteristike tačke

Sve tačke u prostoru su podeljene na tačke posebnih i opštih odredbi.

Privatne pozicije. Tačke koje pripadaju projekcijskom aparatu nazivaju se tačke određene pozicije. To uključuje tačke koje pripadaju ravnima projekcije, osovinama, ishodištu i centrima projekcije. Karakteristične karakteristike tačaka određene pozicije su:

Metamatematički - jedna, dvije ili sve numeričke vrijednosti koordinata jednake su nuli i (ili) beskonačnosti;

Na grafu - dvije ili sve projekcije tačke nalaze se na osi i (ili) se nalaze u beskonačnosti.

Opšte tačke položaja. Tačke opšte pozicije su tačke koje ne pripadaju projekcionom aparatu. Na primjer, tačka A na sl. 1 i 2.

U općenitom slučaju, numeričke vrijednosti koordinata točke karakteriziraju njenu udaljenost od ravnine projekcije: koordinata NS iz aviona π 3; koordinata y iz aviona π 2; koordinata z iz aviona π 1... Treba napomenuti da predznaci na numeričkim vrijednostima koordinata ukazuju na smjer točke koja se udaljava od ravnina projekcije. Ovisno o kombinaciji znakova na numeričkim vrijednostima koordinata točke, ovisi u kojem se oktanu nalazi.

Metoda dvije slike

U praksi se, pored metode pune projekcije, koristi i metoda dvije slike. Razlikuje se po tome što ova metoda isključuje treću projekciju objekta. Za dobijanje projekcijskog aparata po metodi dve slike, profilna ravan projekcija sa svojim projekcijskim centrom isključena je iz aparata pune projekcije (slika 3). Osim toga, na osi 0X ishodište je dodijeljeno (tačka 0 ) i od njega okomito na osu 0X u ravnima projekcije π 1 i π 2 crtati ose 0Y i 0Z respektivno.

U ovom aparatu ceo prostor je podeljen u četiri kvadranta. Na sl. 3 označeni su rimskim brojevima.

Projekcione ravni se smatraju neprozirnim, a posmatrač je uvek unutra I th kvadrant.

Razmotrimo rad uređaja na primjeru projekcije tačke A.

Iz centara projekcije S 1 i S 2 projekcijske zrake izlaze l 1 i l 2... Ovi zraci prolaze kroz tačku A a sijeku se sa ravnima projekcije formiraju njegove projekcije:

- A 1- horizontalna projekcija tačke A;

- A 2- frontalna projekcija tačke A.

Da dobijem tačku A(Sl. 4), u projekcijskom uređaju (Sl. 3) ravan π 1 sa dobijenom projekcijom tačke A 1 rotirati u smjeru kazaljke na satu oko ose 0X, prije nego što ga poravnate s ravninom π 2... Smjer rotacije aviona π 1 je prikazano na sl. 3 strelice. U ovom slučaju, na dijagramu tačke dobivene metodom dvije slike, ostaje samo jedna vertikalno komunikacijska linija A 1 A 2.

U praksi, crtanje tačke A(x A, y A, z A) vrši se numeričkim vrijednostima njegovih koordinata x A, y A i z A u sledećem redosledu (sl. 4).

1. Nacrtana je os OX a ishodište je dodijeljeno (tačka 0 ).

2. Na osi OX numerička vrijednost koordinate je odgođena x A bodova A i dobiti poziciju tačke Sjekira.

3. Prolazna tačka Sjekira okomito na osu OX povlači se vertikalna komunikacijska linija.

4. Na vertikalnoj komunikacijskoj liniji od tačke Sjekira u smjeru ose OY numerička vrijednost koordinate je odgođena y A bodova A i određuje se položaj horizontalne projekcije tačke A 1 OY nije ucrtan, ali se pretpostavlja da se njegove pozitivne vrijednosti nalaze ispod ose OX a negativni su veći.

5. Na vertikalnoj komunikacijskoj liniji od tačke Sjekira u smjeru ose OZ numerička vrijednost koordinate je odgođena z A bodova A i određuje se položaj frontalne projekcije tačke A 2 na dijagramu. Treba napomenuti da je na dijagramu os OZ nije ucrtan, ali se pretpostavlja da se njegove pozitivne vrijednosti nalaze iznad ose OX a negativni su niži.

Konkursne tačke

Tačke na jednoj projekcijskoj zraki nazivaju se konkurentske tačke. Imaju zajedničku projekciju u pravcu zraka projekcije, tj. njihove projekcije su identične. Karakteristična karakteristika konkurentskih tačaka na parceli je identična podudarnost njihovih istoimenih projekcija. Konkurencija je u vidljivosti ovih projekcija u odnosu na posmatrača. Drugim riječima, u prostoru je za posmatrača jedna od tačaka vidljiva, druga nije. I, shodno tome, na crtežu: jedna od projekcija konkurentskih tačaka je vidljiva, a projekcija druge tačke je nevidljiva.

Na modelu prostorne projekcije (sl. 5) dvije konkurentske tačke A i V vidljiva tačka A prema dvije međusobno komplementarne karakteristike. Sudeći po lancu S 1 → A → B tačka A bliže posmatraču od tačke V... I, shodno tome, dalje od ravni projekcije π 1(oni. z A > z A).

Rice. Slika 5 Slika 6

Ako je sama tačka vidljiva A, tada je vidljiva i njegova projekcija A 1... S obzirom na projekciju koja se s njim poklapa B 1... Radi jasnoće i, ako je potrebno, na dijagramu, nevidljive projekcije tačaka obično se stavljaju u zagrade.

Uklonimo tačke na modelu A i V... Njihove podudarne projekcije na ravni će ostati π 1 i odvojene projekcije - na π 2... Ostavimo uslovno frontalnu projekciju posmatrača (⇩) koja se nalazi u centru projekcije S 1... Zatim duž lanca slika ⇩ → A 2 → B 2 o tome će se moći suditi z A > z B i da je sama tačka vidljiva A i njegovu projekciju A 1.

Razmotrite konkurentske tačke na sličan način WITH i D očigledno u odnosu na ravan π 2. Budući da je zajednička projekcija zraka ovih tačaka l 2 paralelno sa osom 0Y, zatim znak vidljivosti konkurentskih tačaka WITH i D je definisana nejednakošću y C> y D... Dakle, poenta D zatvoreno tačkom WITH i, shodno tome, projekcija tačke D 2 biće pokriveni projekcijom tačke C 2 na površini π 2.

Razmotrite kako se određuje vidljivost konkurentskih tačaka na kompozitnom crtežu (slika 6).

Na osnovu koincidentnih projekcija A 1≡U 1 same tačke A i V nalaze se na jednoj projekcijskoj zraci paralelnoj sa osom 0Z... To znači da su koordinate predmet poređenja z A i z B ove tačke. Za ovo koristimo ravan frontalne projekcije sa odvojenim slikama tačke. U ovom slučaju z A > z B... Iz ovoga proizilazi da je vidljiva projekcija A 1.

Poeni C i D na razmatranom kompleksnom crtežu (slika 6) takođe se nalaze na jednoj projekcijskoj zraci, ali samo paralelno sa osom 0Y... Dakle, iz poređenja y C> y D zaključujemo da je projekcija C 2 vidljiva.

Opšte pravilo. Vidljivost za koincidentne projekcije konkurentskih tačaka utvrđuje se poređenjem koordinata ovih tačaka u pravcu zajedničkog projekcijskog zraka. Vidljiva je projekcija tačke u kojoj je ova koordinata veća. U ovom slučaju, poređenje koordinata se vrši na ravni projekcije sa odvojenim slikama tačaka.

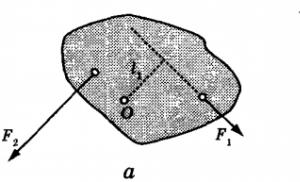
Razmotrimo projekciju tačaka na dvije ravni, za koje uzimamo dvije okomite ravni (slika 4), koje ćemo nazvati horizontalna frontalna i ravni. Linija presjeka ovih ravnina naziva se osa projekcije. Na razmatrane ravni projektiramo jednu tačku A pomoću projekcije na ravan. Da biste to učinili, potrebno je spustiti okomite Aa i A iz ove tačke na razmatrane ravnine.

Projekcija na horizontalnu ravan naziva se horizontalna projekcija bodova A i projekcija a? na frontalnoj ravni se zove frontalna projekcija.

Tačke koje se projektuju obično se označavaju u deskriptivnoj geometriji velikim latiničnim slovima. A, B, C... Mala slova se koriste za označavanje horizontalnih projekcija tačaka. a, b, c... Frontalne projekcije su označene malim slovima sa crtom na vrhu a ?, b ?, c?…

Koristi se i oznaka tačaka rimskim brojevima I, II, ..., a za njihove projekcije - arapskim brojevima 1, 2 ... i 1 ?, 2? ...

Kada okrenete horizontalnu ravan za 90°, možete dobiti crtež na kojem su obje ravni u istoj ravni (slika 5). Ova slika se zove point plot.

Kroz okomite linije Aa i ha? nacrtati ravan (slika 4). Rezultirajuća ravan je okomita na frontalnu i horizontalnu ravninu, jer sadrži okomite na te ravni. Dakle, ova ravan je okomita na liniju preseka ravnina. Rezultirajuća ravna linija siječe horizontalnu ravninu u pravoj liniji aa x, a frontalna ravan - u pravoj liniji huh NS. Pravo aah i huh x su okomite na osu presjeka ravnina. To je Aaah? je pravougaonik.

Prilikom kombiniranja ravnine horizontalne i frontalne projekcije a i a? ležat će na istoj okomici na osu presjeka ravnina, jer kada se horizontalna ravnina rotira, okomitost segmenata aa x i huh x neće biti prekršen.

Dobijamo to na dijagramu projekcije a i a? neka tačka A uvijek leže na istoj okomiti na osu presjeka ravnina.

Dvije projekcije a i a? neka tačka A može jednoznačno odrediti svoj položaj u prostoru (slika 4). To potvrđuje i činjenica da će pri konstruisanju okomice iz projekcije a na horizontalnu ravan ona prolaziti kroz tačku A. Na isti način okomita iz projekcije a? do frontalne ravni će proći kroz tačku A, odnosno tačka A nalazi se istovremeno na dvije određene linije. Tačka A je njihova presječna tačka, odnosno određena je.

Zamislite pravougaonik Aaa NS a?(slika 5), ​​za koje su tačne sljedeće tvrdnje:

1) Udaljenost tačke A od frontalne ravni jednaka je udaljenosti njegove horizontalne projekcije a od ose presjeka ravnina, tj.

ha? = aa NS;

2) udaljenost tačke A od horizontalne ravni projekcije jednaka je udaljenosti njegove frontalne projekcije a? od ose preseka ravni, tj.

Aa = huh NS.

Drugim riječima, čak i bez same tačke na dijagramu, koristeći samo dvije njene projekcije, možete saznati na kojoj se udaljenosti od svake od ravni projekcije data tačka nalazi.

Presjek dvije ravni projekcije dijeli prostor na četiri dijela, koji se nazivaju četvrtine(sl. 6).

Osa presjeka ravnina dijeli horizontalnu ravan na dvije četvrtine - prednju i stražnju, a frontalnu ravan - na gornju i donju četvrtinu. Granicama prve četvrtine smatraju se gornji dio frontalne ravni i prednji dio horizontalne ravni.

Prilikom prijema dijagrama, horizontalna ravan se rotira i poravnava sa frontalnom ravninom (slika 7). U ovom slučaju, prednji dio horizontalne ravnine će se poklopiti s donjim dijelom frontalne ravnine, a stražnji dio horizontalne ravnine - s gornjim dijelom frontalne ravnine.

Slike 8-11 prikazuju tačke A, B, C, D koje se nalaze u različitim četvrtima prostora. Tačka A je u prvoj četvrtini, tačka B u drugoj, tačka C u trećoj i tačka D u četvrtoj.

Kada se bodovi nalaze u prvoj ili četvrtoj četvrtini, njihova horizontalne projekcije nalaze se na prednjoj strani horizontalne ravni, a na ploci će ležati ispod ose presjeka ravnina. Kada se tačka nalazi u drugoj ili trećoj četvrtini, njena horizontalna projekcija će ležati na zadnjoj strani horizontalne ravni, a na grafu će biti iznad ose preseka ravni.

Frontalne projekcije tačke koje se nalaze u prvoj ili drugoj četvrti ležat će na gornjem dijelu frontalne ravni, a na plohi će biti iznad ose presjeka ravnina. Kada se tačka nalazi u trećoj ili četvrtoj četvrtini, njena frontalna projekcija je ispod ose preseka ravni.

Najčešće se u stvarnim konstrukcijama figura postavlja u prvu četvrtinu prostora.

U nekim posebnim slučajevima, tačka ( E) može ležati na horizontalnoj ravni (slika 12). U ovom slučaju, njegova horizontalna projekcija e i sama tačka će se poklopiti. Frontalna projekcija takve tačke nalazit će se na osi presjeka ravnina.

U slučaju kada je tačka TO leži na frontalnoj ravni (slika 13), njena horizontalna projekcija k leži na osi presjeka ravnina, a frontalni k? prikazuje stvarnu lokaciju ove tačke.

Za takve tačke, znak da leži na jednoj od ravni projekcije je da je jedna od njegovih projekcija na osi preseka ravnina.

Ako tačka leži na osi presjeka ravnina projekcije, ona i obje njene projekcije se poklapaju.

Kada tačka ne leži na ravni projekcije, zove se tačka opšte pozicije... U nastavku, ako nema posebnih oznaka, tačka koja se razmatra je tačka u opštem položaju.

2. Nedostatak osi projekcije

Da bismo objasnili kako dobiti projekcije tačke na modelu okomitu na ravan projekcije (slika 4), potrebno je uzeti komad debelog papira u obliku izduženog pravokutnika. Treba ga savijati između projekcija. Linija pregiba će predstavljati osu presjeka ravnina. Ako se nakon toga presavijeni komad papira ponovo ispravi, dobijamo dijagram sličan onom prikazanom na slici.

Kombinovanjem dve projekcijske ravni sa ravninom crteža ne možete da prikažete liniju pregiba, odnosno ne možete nacrtati osu preseka ravnina na grafu.

Kada gradite na parceli, uvijek treba postaviti projekcije a i a? tačka A na jednoj vertikalnoj liniji (sl. 14), koja je okomita na osu preseka ravnina. Stoga, čak i ako položaj ose presjeka ravnina ostane nedefiniran, ali je njegov smjer određen, os presjeka ravnina može biti na grafu samo okomita na pravu liniju ah?.

Ako na dijagramu tačke ne postoji os projekcije, kao na prvoj slici 14a, možete prikazati položaj ove tačke u prostoru. Da biste to učinili, nacrtajte bilo gdje okomito na pravu liniju ah? os projekcije, kao na drugoj slici (slika 14) i savijte crtež duž ove ose. Ako vratimo okomice u tačkama a i a? prije nego što se ukrste, možete dobiti poen A... Promjenom položaja osi projekcije dobijaju se različiti položaji tačke u odnosu na ravni projekcije, ali nesigurnost položaja osi projekcije ne utiče na relativni položaj više tačaka ili figura u prostoru.

3. Projekcije tačke na tri projekcijske ravni

Uzmite u obzir profilnu ravan projekcija. Projekcije na dvije okomite ravni obično određuju položaj figure i omogućavaju da se sazna njena stvarna veličina i oblik. Ali postoje trenuci kada dvije projekcije nisu dovoljne. Zatim se primjenjuje konstrukcija treće projekcije.

Treća ravan projekcije nacrtana je tako da je istovremeno okomita na obje ravni projekcije (sl. 15). Treća ravan se obično naziva profil.

U takvim konstrukcijama naziva se zajednička ravna linija horizontalne i frontalne ravnine osa NS , zajednička ravna linija horizontalne i profilne ravni - osa at , a zajednička ravna linija frontalne i profilne ravni je osa z ... Poenta O koja pripada sve tri ravni naziva se početna tačka.

Slika 15a prikazuje tačku A i njegove tri projekcije. Projekcija na ravan profila ( a??) su pozvani projekcija profila i označiti a??.

Da se dobije dijagram tačke A, koji se sastoji od tri projekcije a, a a, potrebno je iseći triedar koji formiraju sve ravni duž y-ose (slika 15b) i spojiti sve ove ravni sa ravninom frontalne projekcije. Horizontalna ravnina mora biti rotirana oko ose NS, a ravan profila je oko ose z u smjeru označenom strelicom na slici 15.

Slika 16 prikazuje položaj projekcija ha? i a?? bodova A, koji je rezultat poravnanja sve tri ravnine sa ravninom crteža.

Kao rezultat rezanja, y-osa se pojavljuje na parceli na dva različita mjesta. Na horizontalnoj ravni (slika 16) zauzima okomit položaj (okomito na osu NS), a na ravnini profila - horizontalno (okomito na os z).

Slika 16 prikazuje tri projekcije ha? i a?? tačke A imaju strogo definisanu poziciju na dijagramu i podležu nedvosmislenim uslovima:

a i a? uvijek moraju biti smješteni na istoj vertikalnoj liniji okomitoj na os NS;

a? i a?? mora uvijek biti na istoj horizontalnoj liniji okomitoj na os z;

3) pri crtanju kroz horizontalnu projekciju i horizontalnu liniju i kroz profilnu projekciju a??- okomita prava linija, konstruisane prave se moraju seći na simetrali ugla između osa projekcije, budući da je slika Oa at a 0 a n - kvadrat.

Prilikom konstruisanja tri projekcije tačke potrebno je provjeriti ispunjenost sva tri uslova za svaku tačku.

4. Koordinate tačaka

Položaj tačke u prostoru može se odrediti pomoću tri broja koja se nazivaju njenim koordinate... Svaka koordinata odgovara udaljenosti tačke od neke ravni projekcije.

Definisana udaljenost tačke A na ravninu profila je koordinata NS, pri čemu NS = ha?(Sl. 15), udaljenost do frontalne ravni je koordinata y, a y = ha?, a udaljenost do horizontalne ravni je koordinata z, pri čemu z = aa.

Na slici 15 tačka A zauzima širinu pravougaonog paralelepipeda, a mere ovog paralelepipeda odgovaraju koordinatama ove tačke, odnosno svaka od koordinata je prikazana na slici 15 četiri puta, tj.

x = a? A = Oa x = a y a = a z a ?;

y = a? A = Oa y = a x a = a z a ?;

z = aA = Oa z = a x a? = a y a ?.

Na dijagramu (slika 16), koordinate x i z pojavljuju se tri puta:

x = a z a? = Oa x = a y a,

z = a x a? = Oa z = a y a ?.

Svi segmenti koji odgovaraju koordinatama NS(ili z) su paralelne jedna s drugom. Koordinate at dvaput predstavljen vertikalnom osom:

y = Oa y = a x a

i dva puta - vodoravno:

y = Oa y = a z a ?.

Ova razlika se pojavila zbog činjenice da je y-osa prisutna na grafu u dva različita položaja.

Treba napomenuti da je položaj svake projekcije na dijagramu određen samo dvije koordinate, i to:

1) horizontalne - koordinate NS i at,

2) frontalni - koordinate x i z,

3) profil - koordinate at i z.

Korištenje koordinata x, y i z, možete izgraditi projekcije tačke na parceli.

Ako je tačka A određena koordinatama, njihov zapis se utvrđuje na sljedeći način: A ( NS; y; z).

Prilikom konstruisanja projekcije tačke A potrebno je provjeriti ispunjenost sljedećih uslova:

1) horizontalna i frontalna projekcija a i a? NS NS;

2) frontalna i profilna projekcija a? i a? moraju biti smješteni na istoj okomiti na os z, budući da imaju zajedničku koordinatu z;

3) horizontalna projekcija i takođe uklonjena sa ose NS kao projekcija profila a uklonjen sa ose z od projekcije ah? i ha? imaju zajedničku koordinatu at.

Ako tačka leži u nekoj od ravni projekcije, tada je jedna od njenih koordinata nula.

Kada tačka leži na osi projekcije, njene dve koordinate su nula.

Ako tačka leži u početku, sve tri njene koordinate su nula.

Prilikom rješavanja geometrijskih problema u prostoru često se javlja problem određivanja udaljenosti između ravnine i tačke. U nekim slučajevima to je neophodno za sveobuhvatno rješenje. Ova vrijednost se može izračunati pronalaženjem projekcije na ravan tačke. Razmotrimo ovo pitanje detaljnije u članku.

Jednačina za opisivanje ravni

Prije nego što nastavite s razmatranjem pitanja kako pronaći projekciju točke na ravninu, trebali biste se upoznati s vrstama jednadžbi koje definiraju potonju u trodimenzionalnom prostoru. Više detalja u nastavku.

Opća jednačina koja definira sve tačke koje pripadaju datoj ravni je sljedeća:

A * x + B * y + C * z + D = 0.

Prva tri koeficijenta su koordinate vektora, koji se naziva vodičem za ravan. Ona se poklapa sa normalom za njega, odnosno okomita je. Ovaj vektor je označen sa n¯ (A; B; C). Slobodni koeficijent D je jedinstveno određen iz znanja o koordinatama bilo koje tačke koja pripada ravni.

Pojam projekcije tačke i njen proračun

Pretpostavimo da su date neka tačka P (x 1; y 1; z 1) i ravan. Definisano je opštom jednačinom. Ako povučemo okomitu pravu iz P na datu ravan, onda je očito da će ona presjeći potonju u jednoj određenoj tački Q (x 2; y 2; z 2). Q se naziva projekcija P na dotičnu ravan. Dužina segmenta PQ naziva se rastojanje od tačke P do ravni. Dakle, sam PQ je okomit na ravan.

Kako možete pronaći koordinate projekcije tačke na ravan? Ovo nije teško uraditi. Prvo morate nacrtati jednadžbu za pravu liniju koja će biti okomita na ravan. Njoj će pripadati tačka P. Pošto vektor normale n¯ (A; B; C) ove prave mora biti paralelan, jednačina za nju u odgovarajućem obliku će se napisati na sledeći način:

(x; y; z) = (x 1; y 1; z 1) + λ * (A; B; C).

Gdje je λ realan broj, koji se obično naziva parametrom jednačine. Promjenom možete dobiti bilo koju tačku prave linije.

Nakon što je napisana vektorska jednadžba za pravu okomitu na ravan, potrebno je pronaći zajedničku presječnu točku za razmatrane geometrijske objekte. Njegove koordinate će biti projekcija P. Pošto moraju zadovoljiti obje jednakosti (za pravu i za ravan), problem se svodi na rješavanje odgovarajućeg sistema linearnih jednačina.

Koncept projekcije se često koristi prilikom proučavanja crteža. Oni prikazuju bočne i horizontalne projekcije dijela na ravnine zy, zx i xy.

Izračunavanje udaljenosti od ravni do tačke

Kao što je gore navedeno, poznavanje koordinata projekcije na ravan točke omogućava vam da odredite udaljenost između njih. Koristeći notaciju uvedenu u prethodnom dijelu, nalazimo da je tražena udaljenost jednaka dužini segmenta PQ. Da biste ga izračunali, dovoljno je pronaći koordinate vektora PQ¯, a zatim izračunati njegov modul po dobro poznatoj formuli. Konačni izraz za d udaljenost između P tačke i ravni ima oblik:

d = |PQ¯ | = √ ((x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2).

Rezultirajuća d vrijednost je predstavljena u jedinicama koje specificiraju trenutni Dekartov koordinatni sistem xyz.

Primjer zadatka

Pretpostavimo da postoji tačka N (0; -2; 3) i ravan, koja je opisana sledećom jednačinom:

Potrebno je pronaći tačke projekcije na ravan i izračunati udaljenost između njih.

Najprije ćemo formulirati jednadžbu prave linije koja siječe ravan pod uglom od 90 o. Imamo:

(x; y; z) = (0; -2; 3) + λ * (2; -1; 1).

Eksplicitnim pisanjem ove jednakosti dolazimo do sljedećeg sistema jednačina:

Zamjenom vrijednosti koordinata iz prve tri jednakosti u četvrtu, dobivamo vrijednost λ, koja određuje koordinate zajedničke točke prave i ravni:

2 * (2 * λ) - (-2 - λ) + λ + 3 + 4 = 0 =>

6 * λ + 9 = 0 =>

λ = 9/6 = 3/2 = 1,5.

Zamijenite pronađeni parametar u i pronađite koordinate projekcije originalne točke na ravan:

(x; y; z) = (0; -2; 3) + 1,5 * (2; -1; 1) = (3; -3,5; 4,5).

Za izračunavanje udaljenosti između geometrijskih objekata navedenih u izjavi problema, primjenjujemo formulu za d:

d = √ ((3 - 0) 2 + (-3,5 + 2) 2 + (4,5 - 3) 2) = 3,674.

U ovom zadatku pokazali smo kako pronaći projekciju tačke na proizvoljnu ravan i kako izračunati udaljenost između njih.

Proučavanje svojstava figura u prostoru i na ravni nemoguće je bez poznavanja udaljenosti između tačke i takvih geometrijskih objekata kao što su prava linija i ravan. U ovom članku ćemo pokazati kako pronaći ove udaljenosti s obzirom na projekciju točke na ravan i na pravu liniju.

Jednadžba prave linije za dvodimenzionalne i trodimenzionalne prostore

Izračunavanje udaljenosti tačke do prave linije i ravni vrši se pomoću njene projekcije na ove objekte. Da biste mogli pronaći ove projekcije, trebate znati u kom obliku su date jednačine za prave i ravni. Počnimo s prvima.

Prava linija je skup tačaka od kojih se svaka može dobiti iz prethodne prenošenjem na vektore koji su međusobno paralelni. Na primjer, postoji tačka M i N. Vektor MN¯ koji ih povezuje preslikava M u N. Postoji i treća tačka P. Ako je vektor MP¯ ili NP¯ paralelan sa MN¯, tada sve tri tačke leže na istu pravu liniju i formiraju je.

U zavisnosti od dimenzije prostora, jednačina koja definiše pravu liniju može promeniti svoj oblik. Dakle, dobro poznata linearna zavisnost y koordinate od x u prostoru opisuje ravan koja je paralelna trećoj z-osi. S tim u vezi, u ovom članku ćemo razmotriti samo vektorsku jednadžbu za pravu liniju. Ima isti izgled za ravan i trodimenzionalni prostor.

U prostoru, prava linija se može specificirati sljedećim izrazom:

(x; y; z) = (x 0; y 0; z 0) + α * (a; b; c)

Ovdje vrijednosti koordinata sa nultim indeksima odgovaraju tački koja pripada pravoj liniji, u¯ (a; b; c) su koordinate vektora smjera koji leži na ovoj pravoj liniji, α je proizvoljan realan broj , mijenjajući koje možete dobiti sve tačke prave linije. Ova jednačina se naziva vektorska jednačina.

Često je gornja jednačina napisana u otvorenom obliku:

Na sličan način možete napisati jednačinu za pravu liniju koja se nalazi u ravni, odnosno u dvodimenzionalnom prostoru:

(x; y) = (x 0; y 0) + α * (a; b);

Jednačina ravnine

Da biste mogli pronaći udaljenost od tačke do ravni projekcije, morate znati kako je ta ravan definirana. Baš kao i prava linija, može se predstaviti na nekoliko načina. Ovdje ćemo razmotriti samo jednu: opštu jednačinu.

Pretpostavimo da tačka M (x 0; y 0; z 0) pripada ravni, a vektor n¯ (A; B; C) je okomit na nju, tada za sve tačke (x; y; z) od ravni jednakost će biti tačna:

A * x + B * y + C * z + D = 0, gdje je D = -1 * (A * x 0 + B * y 0 + C * z 0)

Treba imati na umu da su u ovoj opštoj jednačini ravni koeficijenti A, B i C koordinate vektora normalne na ravan.

Izračunavanje udaljenosti po koordinatama

Prije nego što pređemo na razmatranje projekcija na ravan tačke i na pravu liniju, treba se prisjetiti kako treba izračunati udaljenost između dvije poznate tačke.

Neka postoje dvije prostorne tačke:

A 1 (x 1; y 1; z 1) i A 2 (x 2; y 2; z 2)

Tada se udaljenost između njih izračunava po formuli:

A 1 A 2 = √ ((x 2 -x 1) 2 + (y 2 -y 1) 2 + (z 2 -z 1) 2)

Ovaj izraz se takođe koristi za određivanje dužine vektora A 1 A 2 ¯.

Za slučaj na ravni, kada su dve tačke date samo parom koordinata, može se napisati slična jednakost bez prisustva člana sa z u njoj:

A 1 A 2 = √ ((x 2 -x 1) 2 + (y 2 -y 1) 2)

Sada ćemo razmotriti različite slučajeve projekcije na ravan tačke na pravu i na ravan u prostoru.

Tačka, linija i udaljenost između njih

Pretpostavimo da postoji neka tačka i prava linija:

P 2 (x 1; y 1);

(x; y) = (x 0; y 0) + α * (a; b)

Udaljenost između ovih geometrijskih objekata odgovaraće dužini vektora čiji početak leži u tački P 2, a kraj u takvoj tački P na navedenoj pravoj liniji, za koju vektor P 2 P ¯ od ova prava linija je okomita. Tačka P naziva se projekcija tačke P 2 na pravu koja se razmatra.

Ispod je slika koja prikazuje tačku P 2, njenu udaljenost d do prave linije, kao i vektor pravca v 1 ¯. Takođe, na pravoj liniji se bira proizvoljna tačka P 1 i iz nje se povlači vektor do P 2. Tačka P ovde se poklapa sa mestom gde okomita seče pravu.

Vidi se da narandžasta i crvena strelica formiraju paralelogram čije su stranice vektori P 1 P 2 ¯ i v 1 ¯, a visina je d. Iz geometrije je poznato da da bi se pronašla visina paralelograma, njegovu površinu treba podijeliti s dužinom osnove na koju se spušta okomica. Budući da se površina paralelograma izračunava kao poprečni proizvod njegovih stranica, dobijamo formulu za izračunavanje d:

d = || / |v 1 ¯ |

Svi vektori i koordinate tačaka u ovom izrazu su poznati, tako da ga možete koristiti bez izvođenja ikakvih transformacija.

Ovaj problem je mogao biti riješen drugačije. Da biste to učinili, zapišite dvije jednačine:

• skalarni proizvod P 2 P ¯ sa v 1 ¯ mora biti jednak nuli, pošto su ovi vektori međusobno okomiti;
• koordinate tačke P moraju zadovoljiti jednačinu prave.

Ove jednadžbe su dovoljne da se pronađu koordinate P, a zatim i dužina d prema formuli datoj u prethodnom pasusu.

Problem nalaženja udaljenosti između prave i tačke

Hajde da pokažemo kako koristiti ove teorijske informacije za rješavanje određenog problema. Pretpostavimo da su poznate sljedeće tačke i prava:

(x; y) = (3; 1) - α * (0; 2)

Potrebno je pronaći tačke projekcije na pravu liniju na ravan, kao i rastojanje od M do prave.

Označimo projekciju koju treba naći tačkom M 1 (x 1; y 1). Ovaj problem ćemo riješiti na dva načina, opisana u prethodnom pasusu.

Metoda 1. Vektor smjera v 1 ¯ koordinate ima (0; 2). Da biste napravili paralelogram, odaberite tačku koja pripada pravoj liniji. Na primjer, tačka sa koordinatama (3; 1). Tada će vektor druge strane paralelograma imati koordinate:

(5; -3) - (3; 1) = (2; -4)

Sada je potrebno izračunati proizvod vektora koji definiraju stranice paralelograma:

Zamjenom ove vrijednosti u formulu, dobijamo udaljenost d od M do prave linije:

Metod 2. Nađimo sada na drugačiji način ne samo rastojanje, već i koordinate projekcije M na pravu liniju, kako to zahtijeva uslov zadatka. Kao što je već spomenuto, da bi se riješio problem, potrebno je sastaviti sistem jednačina. Poprimiće oblik:

(x 1 -5) * 0 + (y 1 +3) * 2 = 0;

(x 1; y 1) = (3; 1) -α * (0; 2)

Rešavamo ovaj sistem:

Projekcija koordinatnog početka ima M 1 (3; -3). Tada je tražena udaljenost jednaka:

d = |MM 1 ¯ | = √ (4 + 0) = 2

Kao što vidite, obje metode rješavanja dale su isti rezultat, što ukazuje na ispravnost izvedenih matematičkih operacija.

Projekcija od tačke do ravni

Sada razmotrimo šta je projekcija tačke u prostoru na određenu ravan. Lako je pretpostaviti da je i ova projekcija tačka, koja zajedno sa originalnom čini vektor okomit na ravan.

Pretpostavimo da projekcija na ravan tačke M ima sledeće koordinate:

Sama ravan je opisana jednadžbom:

A * x + B * y + C * z + D = 0

Na osnovu ovih podataka možemo formulisati jednačinu prave linije koja siječe ravan pod pravim uglom i prolazi kroz M i M 1:

(x; y; z) = (x 0; y 0; z 0) + α * (A; B; C)

Ovdje su varijable sa nultim indeksom koordinate tačke M. Položaj na ravni tačke M 1 može se izračunati na osnovu činjenice da njene koordinate moraju zadovoljiti obje napisane jednačine. Ako su ove jednadžbe nedovoljne za rješavanje problema, onda se može koristiti uvjet paralelizma MM 1 ¯ i vektor smjera za datu ravan.

Očigledno, projekcija tačke koja pripada ravni poklapa se sama sa sobom, a odgovarajuća udaljenost je nula.

Problem tačke i ravni

Neka su data tačka M (1; -1; 3) i ravan, što je opisano sledećom opštom jednačinom:

Izračunajte koordinate projekcije na ravan tačke i izračunajte udaljenost između ovih geometrijskih objekata.

Za početak, konstruiramo jednadžbu prave linije koja prolazi kroz M i okomita na naznačenu ravan. Izgleda:

(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)

Označimo tačku u kojoj ova prava seče ravan, M 1. Jednakosti za ravan i pravu moraju biti ispunjene ako se u njih umetnu koordinate M 1. Eksplicitno zapisujući jednačinu prave linije, dobijamo sledeće četiri jednakosti:

X 1 + 3 * y 1 -2 * z 1 + 4 = 0;

y 1 = -1 + 3 * α;

Iz posljednje jednakosti dobijamo parametar α, zatim ga zamjenjujemo u pretposljednji i u drugi izraz dobijamo:

y 1 = -1 + 3 * (3-z 1) / 2 = -3 / 2 * z 1 + 3,5;

x 1 = 1 - (3-z 1) / 2 = 1/2 * z 1 - 1/2

Zamijenimo izraz za y 1 i x 1 u jednadžbu za ravan, imamo:

1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3,5) -2 * z 1 + 4 = 0

Odakle dobijamo:

y 1 = -3 / 2 * 15/7 + 3,5 = 2/7;

x 1 = 1/2 * 15/7 - 1/2 = 4/7

Utvrdili smo da projekcija tačke M na datu ravan odgovara koordinatama (4/7; 2/7; 15/7).

Sada izračunajmo udaljenost | MM 1 ¯ |. Koordinate odgovarajućeg vektora su:

MM 1 ¯ (-3/7; 9/7; -6/7)

Potrebna udaljenost je jednaka:

d = |MM 1 ¯ | = √126 / 7 ≈ 1.6

Tri tačke projekcije

Prilikom izrade crteža često je potrebno dobiti projekcije presjeka na međusobno okomite tri ravni. Stoga je korisno razmotriti kakve će biti projekcije neke tačke M sa koordinatama (x 0; y 0; z 0) na tri koordinatne ravni.

Nije teško pokazati da je xy ravan opisana jednadžbom z = 0, ravan xz odgovara izrazu y = 0, a preostala yz ravan je označena jednakošću x = 0. Lako je pretpostaviti da je projekcije tačke na 3 ravni će biti jednake:

za x = 0: (0; y 0; z 0);

za y = 0: (x 0; 0; z 0);

za z = 0: (x 0; y 0; 0)

Gdje je važno znati projekciju tačke i njenu udaljenost od ravnina?

Određivanje položaja projekcije tačaka na datu ravan je važno pri pronalaženju veličina kao što su površina i zapremina za nagnute prizme i piramide. Na primjer, udaljenost od vrha piramide do ravni baze je visina. Potonji je uključen u formulu za volumen ove figure.

Razmatrane formule i metode za određivanje projekcija i udaljenosti od tačke do prave i ravni su prilično jednostavne. Važno je samo zapamtiti odgovarajuće oblike jednadžbi ravnine i prave, kao i imati dobru prostornu maštu kako biste ih uspješno primijenili.